Physical Review B 99, 104418 (2019)

Nonlinear Transport, Dynamic Ordering, and Clustering for Driven Skyrmions on Random Pinning

C. Reichhardt and C. J. O. Reichhardt

Theoretical Division and Center for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA

(Received 24 August 2018; revised manuscript received 8 January 2019; published 14 March 2019)

Using numerical simulations, we examine the nonlinear dynamics of skyrmions driven over random pinning. For weak pinning, the skyrmions depin elastically, retaining sixfold ordering; however, at the onset of motion there is a dip in the magnitude of the structure factor peaks due to a decrease in positional ordering, indicating that the depinning transition can be detected using the structure factor even within the elastic depinning regime. At higher drives the moving skyrmion lattice regains full ordering. For increasing pinning strength, we find a transition from elastic to plastic depinning that is accompanied by a sharp increase in the depinning threshold due to the proliferation of topological defects, similar to the peak effect found at the elastic to plastic depinning transition in superconducting vortex systems. For strong pinning and strong Magnus force, the skyrmions in the moving phase can form a strongly clustered or phase separated state with highly modulated skyrmion density, similar to that recently observed in continuum-based simulations for strong disorder. As the Magnus force is decreased, the density phase separated state crosses over to a dynamically phase separated state with uniform density but with flow localized in bands of motion, while in the strongly damped limit, both types of phase separated states are lost. In the strong pinning limit, we find highly nonlinear velocity-force curves in the transverse and longitudinal directions, along with distinct regions of negative differential conductivity in the plastic flow regime. The negative differential conductivity is absent in the overdamped limit. The Magnus force is responsible for both the negative differential conductivity and the clustering effects, since it causes faster moving skyrmions to partially rotate around slower moving or pinned skyrmions.

I. INTRODUCTION
II. SIMULATION
III. ELASTIC TO PLASTIC DEPINNING
Nonlinear velocity-force curves
IV. DYNAMICS AS A FUNCTION OF SKYRMION DENSITY
Transverse locking in the elastic depinning regime
V. DYNAMICS AS A FUNCTION OF MAGNUS FORCE
VI. DENSITY PHASE SEPARATION AND DYNAMIC PHASE SEPARATION
VII. DISCUSSION
VIII. SUMMARY
REFERENCES

I. INTRODUCTION

There are a wide variety of systems that can be effectively described as a collection of particles that couple to a randomly disordered substrate [1,2]. Specific examples include vortices in type-II superconductors with naturally occurring defects [3,4,5,6], colloidal particles on disordered landscapes [7,8,9,10,11], pattern forming systems on rough surfaces [12,13,14,15], Wigner crystals in the presence of charged impurities [16,17,18,19], active matter or self-propelled particles in complex environments [20,21], fluid flow over disordered surfaces [22,23,24], granular matter flowing over disordered backgrounds [25], various models of sliding friction [26], dislocation dynamics [27,28], and geological systems such as plate tectonics [29]. Under an applied drive, these systems typically exhibit a pinned phase at low drive that transitions to a sliding state at higher drives, and additional transitions can occur within the sliding state between different types of flowing phases [1,2]. In an elastic depinning transition, the particles keep their same neighbors, while during plastic depinning, the particles exchange neighbors, leading to a proliferation of topological defects in the form of dislocations [1,2,3,30,31]. Some systems can be described in terms of the depinning of polycrystalline states composed of large ordered regions separated by mobile grain boundaries [32], a process that produces distinct transport features compared to strongly disordered systems in which local ordering extends only a few lattice spacings or less [30,32]. These different types of depinning phenomena produce different features in the velocity-force curves, differential conductivity, velocity fluctuation spectra, and global structure of the particles [1,2,3]. Plastic depinning can be followed by a dynamical transition at higher drives from the disordered moving plastic state into a moving crystal [1,3,5] or moving smectic state [33,34,35,36,37], where the system regains considerable ordering when the high velocity motion of the particles reduces the effectiveness of the pinning.

In certain systems such as vortices in type-II superconductors, when the pinning strength is increased or the elastic constant of the vortex lattice is reduced, there can be a transition from elastic to plastic depinning accompanied by a sharp increase in the critical depinning force, called the "peak effect," which is also associated with changes in the shape of the velocity-force curves [2,3,4,38,39]. The velocity typically increases monotonically with driving force F_D when the substrate is disordered; however, the velocity-force curve can be nonlinear and exhibit scaling of the form V ∝ (F_D − F_c)^β, where F_c is the depinning force and the value of β depends on whether the depinning transition is elastic or plastic [1,2,30,31]. If the substrate is periodic, the velocity-force curves can show a decrease in the particle velocity with increasing F_D, giving rise to negative differential conductivity [1]; however, for random substrates, negative differential conductivity is generally not observed.

In 2009, the discovery of skyrmions in chiral magnets opened the study of a new type of particle-like objects that can form an elastic lattice. The initial neutron scattering measurements [40] revealed sixfold ordering, indicating that the skyrmions form a triangular lattice similar to the vortex lattices found in type II superconductors [40]. A short time later, hexagonal skyrmion lattices were directly observed with Lorentz microscopy [41]. Since then, there has been an enormous increase in skyrmion studies, and a variety of new materials have been identified that are capable of supporting skyrmions, including some in which the skyrmions are stable at room temperature [42,43,44,45,46,47]. It was shown that skyrmions can be set into motion by the application of a current, leading to depinning transitions that can be detected via changes in the transport properties [48,49,50,51,52] or through direct imaging [42,44,45,47,53,54,55]. Skyrmions show great promise for numerous applications due to their size and mobility, so understanding their collective dynamics is of key importance for manipulating dense skyrmion arrays [56].

Among systems that undergo nonequilibrium dynamical transitions when driven over quenched disorder, skyrmions exhibit a new class of behavior, since unlike previously studied systems, the topological nature of the skyrmions causes their dynamics to be dominated by a non-dissipative Magnus force [49]. The Magnus force generates a velocity component perpendicular to the net force experienced by the skyrmion, and as a result, the skyrmions move at an angle, called the skyrmion Hall angle θ_sk, to an applied driving force [45,48,49,53,54,55,57,58,59,60]. The Magnus force also strongly modifies the interactions of the skyrmions with pinning sites or barriers. For localized pinning, the Magnus force causes the skyrmion to rotate around the edge of the pinning site, greatly reducing the depinning threshold compared to the overdamped limit. This effect was argued to be one of the reasons that low critical depinning forces have been observed in certain skyrmion systems [45,48,49,49,50,57,58,59,60]. For line defects or spatially extended pinning sites, the skyrmions cannot avoid the pinning by moving around it, so the effective pinning strength remains large even when the Magnus force is finite [61,62,63].

Although the intrinsic skyrmion Hall angle θ^int_sk is a constant determined by the material parameters [32], the measured θ_sk has a strong drive dependence in the presence of pinning, as initially observed in particle-based simulations of skyrmions moving in random [58,64,65] and periodic pinning arrays [66]. At the depinning threshold, θ_sk ≈ 0, and as the skyrmion velocity increases with increasing drive, θ_sk increases until it saturates at θ_sk=θ_sk^int. Imaging experiments of driven skyrmions reveal a pinned regime, a creep regime where flow occurs in jumps giving θ_sk=0, and a viscous flow regime, where θ_sk increases with increasing F_D and saturates at higher drives [53]. Other experiments have also shown an increase in θ_sk with increasing drive amplitude [54,55]. The drive dependence of θ_sk arises when the Magnus force induces a shift in the motion of the skyrmions as they pass over the pinning sites [58,60,64,65,66], similar to the side jump effect found for an electron scattering off of magnetic impurities. The faster the skyrmion moves, the smaller the shift, as illustrated in particle-based simulations. Continuum-based simulations of driven skyrmions show that in the absence of pinning, θ_sk is constant, while in the presence of pinning, the velocity-force curves are nonlinear and θ_sk increases with increasing drive from zero up to the intrinsic value [45,59], indicating that the particle-based skyrmion simulations successfully capture many features of skyrmion dynamics even though they do not include the internal degrees of freedom of the skyrmions.

Simulations reveal that a transition occurs from a skyrmion crystal to a disordered skyrmion glass state when the pinning strength increases [58]. The crystal depins elastically while the glass depins plastically, but at higher drives the glassy state can dynamically order into a moving skyrmion crystal in a process that is similar to the dynamical ordering transitions observed in the depinning and sliding of vortices [1,3,5,35,36,37,38], colloids [7,9,10], and Wigner crystals [18]. The Magnus force causes the dynamical fluctuations of the moving skyrmions to be much more isotropic than those found in driven overdamped systems, favoring the emergence of an isotropic moving crystal rather than the moving smectic state observed in overdamped systems [65]. Continuum-based simulations of skyrmions on random substrates show similar dynamical ordering under increasing drive when the substrate is only moderately strong [67], and recent experimental neutron scattering data gives evidence for the dynamic ordering of driven skyrmions at high drives [68].

In this work we expand upon our previous particle-based studies of skyrmion dynamics in random pinning, and perform a detailed study of the skyrmion transport, structure, and dynamics as we vary the pinning strength, the ratio of skyrmions to pinning sites, and the ratio of the Magnus force to the damping term. For weak pinning, the skyrmions form a triangular lattice that depins elastically into a moving triangular lattice. Even though there is no structural transition between the pinned and moving states, we find a dip in the weight of the structure factor peaks at the depinning transition due to the deviations of the skyrmions from the lattice positions, followed by a sharpening of the peaks with increasing drive as the effectiveness of the pinning decreases. For increasing pinning strength, a transition from a pinned crystal state to a disordered skyrmion glass occurs that is accompanied by a sharp increase in the critical depinning force F_c, similar to the peak effect phenomenon found at the transition from elastic to plastic depinning in superconducting vortex systems [3,6,38,39]. We also find that the scaling of F_c with the pinning strength F_p crosses over from a quadratic form in the elastic depinning regime to linear scaling in the plastic depinning regime [1,2,4]. These results suggest that a peak effect phenomenon could be a general feature in skyrmion systems that occurs as a function of magnetic field, temperature, or lattice shearing. We observe a change in the scaling of the velocity-force curves across the transition from elastic to plastic depinning, including a region of negative differential mobility, and we explain these effects in terms of the drive dependence of θ_sk. When the pinning strength is high or the Magnus force is large, we observe clustered or density segregated states, where an effective attraction between the skyrmions leads to the formation of dense moving bands separated by low density regions. In recent continuum-based simulations [67], a similar clustered or segregated state appeared at strong pinning and was attributed to the generation of spin waves by the moving skyrmions. In our work, the effective attraction is a result of the Magnus force and occurs when the pinning causes the skyrmions to move at different relative velocities, giving them a tendency to rotate around each other rather than moving parallel to each other. The phase separated states only occur when both the Magnus force and the pinning are sufficiently strong. For weaker pinning, we find a dynamical phase separated state in which the skyrmion density is uniform but there is a coexistence of localized bands of motion and pinned bands.

The paper is organized as follows. In Section II we describe the details of our simulation technique. In Section III we show a transition from elastic to plastic depinning as a function of pinning strength that is accompanied by a sudden change in the critical depinning force, called a peak effect, and we demonstrate that the nonlinearity in the velocity-force curves is distinct from that found for overdamped systems. In Section IV we study the impact of the skyrmion density on the peak effect in the critical depinning force, describe the appearance of transverse locking in the elastic depinning regime, and show crossing of the velocity-force curves in samples on either side of the transition from elastic to plastic depinning. Section V shows how the dynamic phases change when the ratio of the Magnus force to the damping term is varied. The density phase separation and dynamic phase separation that appear for strong pinning and strong Magnus force are described in Section VI. In Section VII we discuss the relevance of our results for the general class of particle based systems with random disorder, as well as the limitations of the model for describing skyrmions in the regime where rigidity of the skyrmion is lost, such as at strong drives and for strong disorder, and we indicate possible future directions of study such as a full micromagnetic treatment or the introduction of additional terms to the particle-based model that can capture inertia, reactive forces, or drive-dependent damping. We summarize our results in Section VIII.

II. SIMULATION

We consider a two-dimensional system of size L ×L with periodic boundaries in the x and y directions containing N rigid skyrmions modeled as point particles. The dynamics of the skyrmions is obtained by integrating a modified version of the Thiele equation that takes into account skyrmion-skyrmion interactions, skyrmion-pin interactions, and an external driving force [10,11,12,22]. The equation of motion of a skyrmion i is

α_d v_i + α_m

×v_i = F^ss_i + F^p_i + F^D ,

(1)

where v_i = d r_i/dt is the skyrmion velocity, α_d is the damping constant which tends to align the skyrmion velocity in the direction of the external forces, and α_m is the strength of the Magnus term which tends to align the skyrmion velocity in the direction perpendicular to the external forces. When both α_d and α_m are finite, the skyrmions move at an angle called the intrinsic skyrmion Hall angle, θ^int_sk = tan⁻¹(α_m/α_d), with respect to an externally applied driving force. The skyrmion-skyrmion interaction is a short range repulsive force of the form F_i^ss = ∑^N_{j ≠ i}K₁(r_ij)∧r_ij, where K₁ is the modified Bessel function, r_ij = |r_i − r_j| is the distance between skyrmion i and skyrmion j, and ∧r_ij=(r_i−r_j)/r_ij [10,21,22]. We place N_p pinning sites in random but non-overlapping positions and model each pinning site as a parabolic trap of range r_p that can exert a maximum pinning force of F_p on a skyrmion of the form F^p_i = ∑_k=1^N_p(F_pr^(p)_ik/r_p)Θ(r_p−r^(p)_ik)∧r^(p)_ik, where r^(p)_ik=|r_i−r^(p)_k| is the distance between skyrmion i and pin k, ∧r^(p)_ik=(r_i−r^(p)_k)/r^(p)_ik, and Θ is the Heaviside step function. The skyrmion density is n_sk=N/L², the pinning density is n_p=N_p/L², L=36 The driving force is F^D = F_D∧x, and we measure the average velocity per skyrmion parallel, 〈V_||〉 = N⁻¹∑^N_i=1 v_i ·∧x, and perpendicular, 〈V_⊥〉 = N⁻¹∑^N_i=1 v_i ·∧y, to the applied drive. We compute the drive-dependent skyrmion Hall angle θ_sk = tan⁻¹(〈V_⊥〉/〈V_||〉), as well as quantities related to the standard deviation of the skyrmion velocities in the parallel and perpendicular directions, δV_|| = √{ [∑_i^N_sk (v_||ⁱ)² − 〈V_||〉²]/N_sk} and δV_⊥ = √{ [∑_i^N_sk (v_⊥ⁱ)² −〈V_⊥〉²]/N_sk}. We note that it is also possible to use an unbiased estimator to obtain the standard deviation, but for consistency, we use the same measure described in our previous study [84]. We also characterize the dynamics as a function of driving force by measuring the structure factor S(k) = L⁻² ∑_i,j e^{i k ·r_ij(t)} and the average fraction of sixfold-coordinated particles P₆=∑_i=1^Nδ(6−z_i), where z_i is the coordination number of skyrmion i obtained from a Voronoi tessellation.

III. ELASTIC TO PLASTIC DEPINNING

Figure 1: (a) S(k₀), the magnitude of the structure factor peak at one of the reciprocal lattice vectors of the skyrmion lattice, vs F_D for the weak pinning case F_p=0.03 in a sample with n_sk=0.16, n_p=0.2, and α_m/α_d=9.95, where the skyrmions form a pinned crystal that depins elastically. (b) The corresponding 〈V_||〉, the average skyrmion velocity parallel to the driving direction, vs F_D. The dip in S(k₀) occurs at the drive for which 〈V_||〉 becomes finite.

Figure 2: S(k) from the system in Fig. 1 with F_p=0.03, n_sk=0.16, n_p=0.2, and α_m/α_d=9.95, where the depinning is elastic and F_c=0.0025. (a) At F_D = 0, there are six sharp peaks indicative of triangular ordering. (b) Just at depinning for F_D/F_c = 1.0, the peaks are still present but there is some smearing. (c) At F_D = 0.008 in the sliding phase, the system is more ordered.

Previous work with the particle-based skyrmion model showed that sufficiently strong pinning causes the system to form a glassy state that depins plastically and then dynamically orders at higher velocities into a moving crystal that can be detected using the structure factor S(k) or P₆ [58,65]. Here we show that even when the pinning is weak, so that the skyrmions form a pinned lattice rather than a glass and retain their sixfold ordering across the depinning transition, there are still detectable changes in the positional ordering of the skyrmions at the depinning transition. In Fig. 1(a) we plot S(k₀), the magnitude of the structure factor at one of the reciprocal lattice vectors k₀ of the skyrmion lattice, versus F_D in a sample with n_sk = 0.16, n_p = 0.2, F_p = 0.03, and α_m/α_d = 9.95, while in Fig. 1(b) we show 〈V_||〉 versus F_D for the same sample. Here the skyrmions depin elastically, so there is no generation of topological defects at the depinning transition, which occurs at F_c = 0.0025. Nevertheless, there is a dip in S(k₀) at the depinning transition, and for F_D > F_c, S(k₀) gradually increases with increasing F_D. In Fig. 2(a) we show S(k) for the same sample at F_D = 0 in the pinned state where there is clear sixfold ordering. Figure 2(b) indicates that at the depinning transition F_D/F_c = 1.0, S(k) maintains its sixfold ordering but the peaks become slightly smeared, while in Fig. 2(c) at F_D = 0.008 in the moving phase, the peaks sharpen again. We find a similar trend for other values of F_p within the elastic depinning regime.

Figure 3: P₆, the fraction of sixfold coordinated skyrmions, vs F_p, measured at the depinning transition for the system in Fig. 1 with n_sk=0.16, n_p=0.2, and α_m/α_d=9.95. (b) The corresponding value of the critical depinning force F_c vs F_p. A transition occurs from elastic depinning, where the skyrmions maintain sixfold ordering, to plastic depinning, marked by a drop in P₆ and a sharp increase in F_c. This behavior is similar to the so-called peak effect in type-II superconductors that appears across the transition from elastic to plastic vortex depinning.

By conducting a series of simulations and examining the velocity-force curves and skyrmion positions for the system in Fig. 1, we construct a plot of the fraction P₆ of particles with sixfold ordering at the depinning transition versus F_p, shown in Fig. 3(a). For F_p < 0.0325, P₆ = 1.0, since the skyrmions retain six neighbors at the elastic depinning transition, while for F_p ≥ 0.0325, P₆ drops since there is a proliferation of topological defects in the form of 5-7 paired dislocations during plastic depinning. In Fig. 3(b) we plot the critical depinning force F_c versus F_p. For the value of F_p at which the drop in P₆ occurs, we find a sharp increase in F_c, indicating that the skyrmions have become much more strongly pinned. The sudden increase in F_c at the transition from elastic depinning to plastic depinning is very similar to the phenomenon known as the peak effect in type-II superconductors, where the weakly pinned elastic vortex lattice undergoes a sharp increase in the depinning force when the vortex lattice disorders and becomes well coupled to the pinning [1,3,6]. In superconducting systems, the strength of the pinning sites is fixed, but the vortex-vortex interaction strength can be modified by changing the temperature or magnetic field, producing a transition to plastic depinning once the vortex-vortex interaction strength drops below the vortex-pin interaction strength. Our results indicate that a similar peak effect phenomenon should be observable in skyrmion systems.

Figure 4: (a) F_c vs F_p plotted on a log-log scale for the system in Fig. 1 with n_sk=0.16, n_p=0.2, and α_m/α_d=9.95. The dashed lines are power law fits to F_c ∝ F_p^α. Blue: α = 2.0 in the elastic depinning regime; red: α = 1.0 in the plastic depinning regime. (b) The corresponding dF_c/dF_p versus F_p curve has a peak near F_p=0.325 at the transition from elastic to plastic depinning. (c) The corresponding P₆ versus F_p curve shows that the elastic to plastic depinning transition coincides with a sharp drop in P₆.

In Fig. 4(a) we plot F_c versus F_p on a log-log scale for the system in Fig. 3, while in Fig. 4(b) we show the corresponding dF_c/dF_p versus F_p curve. In two-dimensional systems that exhibit elastic depinning, the depinning force is expected to scale as F_c ∝ F_p^α with α = 2.0, while in the plastic depinning regime, there is a similar scaling with α = 1.0 [1,4]. In Fig. 4(a), the dashed lines indicate power law fits with α = 2.0 at smaller F_p in the elastic depinning regime and α = 1.0 at larger F_p in the plastic depinning regime, showing good agreement with the expected scalings. At the transition from elastic to plastic depinning, a peak appears in dF_c/dF_p separating a linear increase of dF_c/dF_p with F_p in the elastic depinning regime from a constant dF_c/dF_p in the plastic depinning regime, consistent with the power law scaling in the F_c vs F_p curves. The peak in dF_c/dF_p coincides with a sharp drop in P₆, as shown in Fig. 4(c), and P₆ continues to decrease with increasing F_p throughout the plastic flow regime.

Figure 5: P₆ vs F_D for the system in Fig. 1 with n_sk=0.16, n_p=0.2, and α_m/α_d=9.95 at F_p = 0.03 (red), 0.2 (orange), 0.3, (light blue) and 0.5 (dark blue). For large drives, P₆ increases toward P₆=1.0 as the system dynamically reorders. The plateau in P₆ for F_p=0.5 corresponds to a moving liquid phase in which all the skyrmions are moving but the system is disordered.

In Fig. 5 we plot P₆ versus F_D for the system in Fig. 4 at F_p = 0.03, 0.2, 0.3, and 0.5. For F_p = 0.03, P₆ ≈ 1 at all values of F_D, indicating that the skyrmions retain their sixfold ordering. At F_p = 0.2 where the depinning is plastic, P₆ dips down to P₆=0.475 in the plastic flow phase above depinning but increases to P₆ = 0.93 near F_D = 0.24 when the skyrmions dynamically regain their triangular ordering, similar to what was observed previously [58,65]. For F_p = 0.3 and F_p=0.5, we find an additional shoulder feature above the plastic depinning transition, and for F_p = 0.5 curve this shoulder is followed by a plateau with P₆ ≈ 0.6 over the range 0.5 < F_D < 1.4, above which the system dynamically orders. In the plastic flow phase, there is a coexistence of moving and pinned skyrmions, while in the moving liquid phase on the plateau, all of the skyrmions are moving but the system is disordered.

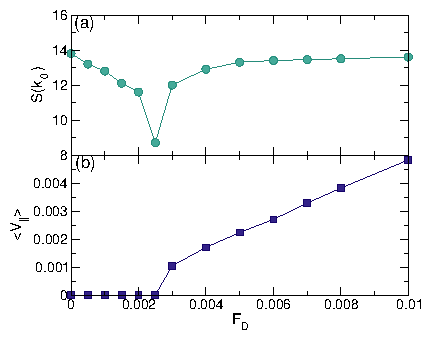
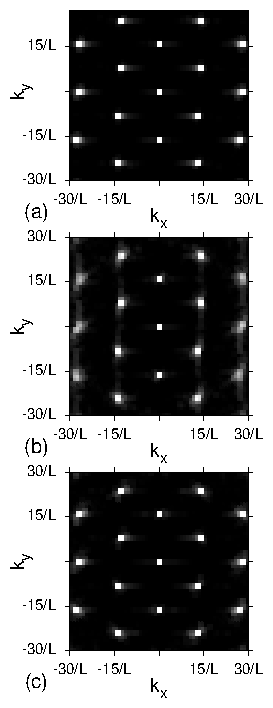
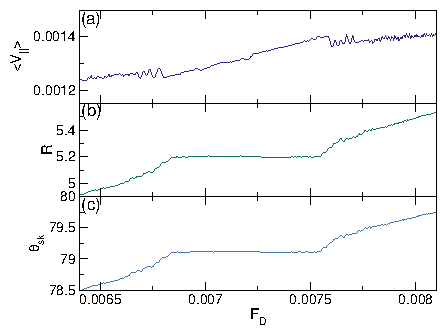
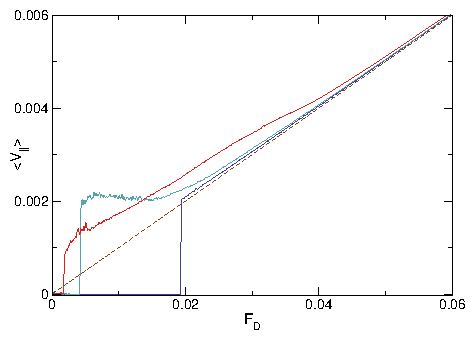
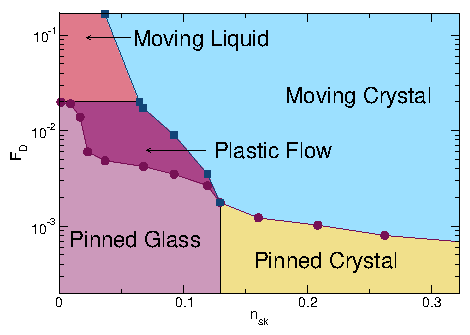
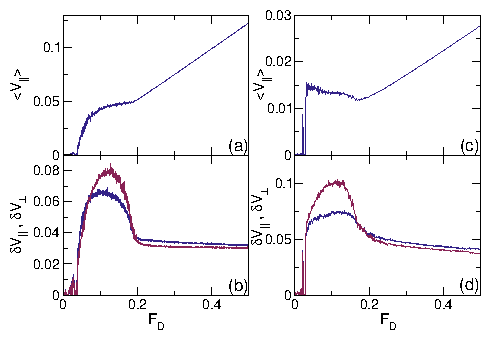
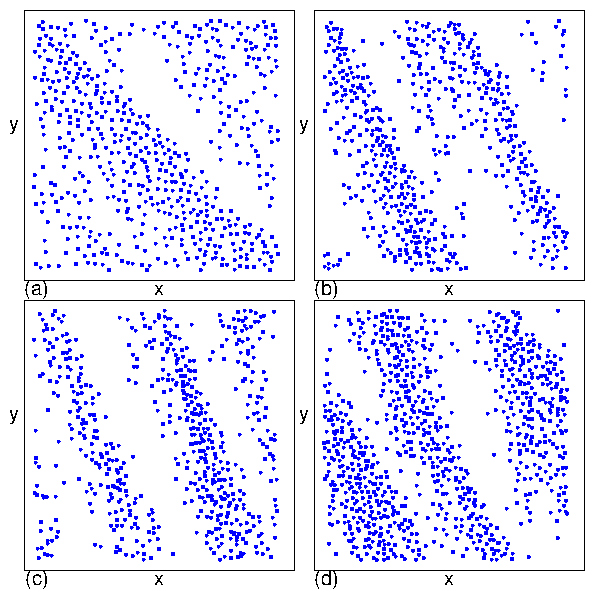
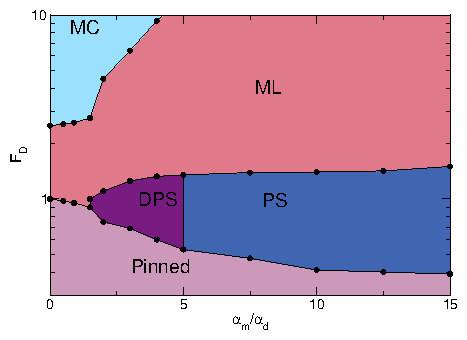
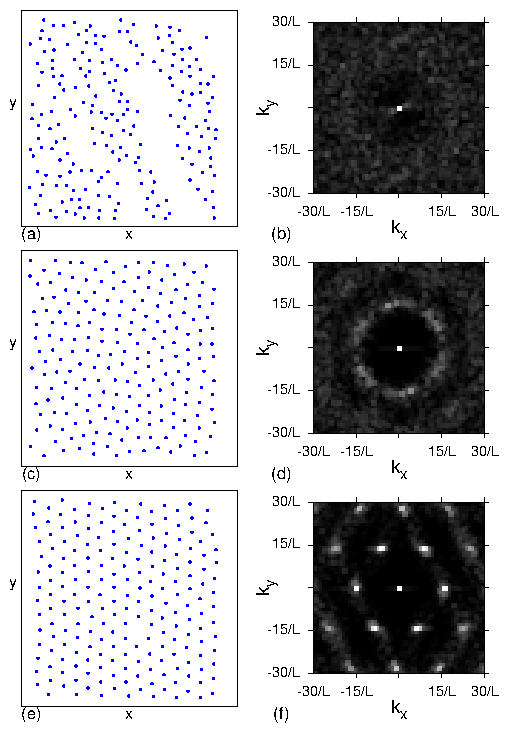
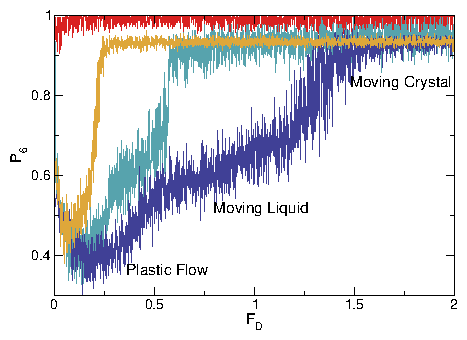
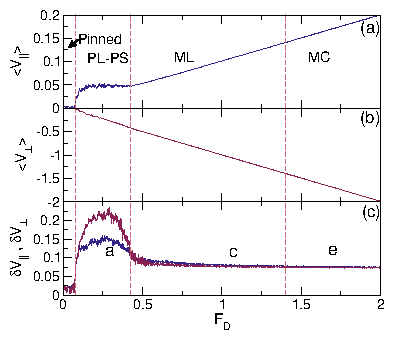
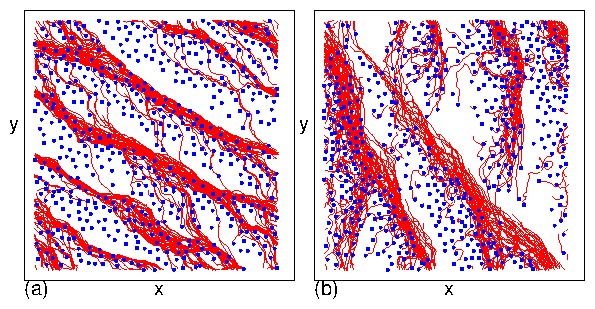
Figure 6: (a, c, e) Real space images of the skyrmion positions and (b, d, f) the corresponding structure factors S(k) for the system in Fig. 5 with n_sk=0.16, n_p=0.2, and α_m/α_d=9.95 at F_p = 0.5. (a,b) At F_D = 0.3, the plastic flow phase contains both pinned and moving skyrmions, and S(k) shows that the structure is random. (c,d) At F_D = 1.1, the skyrmion density is more uniform but the system is still disordered and forms a moving liquid (ML) phase, in which S(k) develops a ringlike feature. 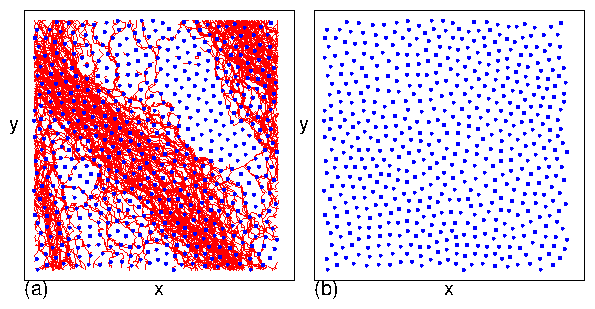(d,e) In the dynamically ordered moving crystal (MC) phase at F_D = 1.75, the skyrmions form a triangular lattice.

In Fig. 6(a,b) we show the skyrmion positions and S(k) for the system in Fig. 5 at F_p = 0.5 in the plastic flow phase at F_D = 0.3, where the skyrmion structure is disordered and there is a tendency for a density phase separation to occur, as discussed in more detail in Section VI. The structure factor is nearly featureless, as expected for a random spatial distribution. Figure 6(c,d) illustrates the skyrmion positions and S(k) for the same system in the moving liquid phase at F_D = 1.1, where the skyrmion density is more uniform but the skyrmion arrangement is still disordered, and where the structure factor contains a ring feature consistent with a liquid state. We note that it is possible to distinguish between different types of random structures. For example, a random arrangement of particles created using a Poisson process gives a structure factor that has finite weight for k → 0, while in an arrangement of particles with what is called a disordered hyperuniform structure, S(k) approaches zero as k → 0 [69]. It has been argued that in the presence of random pinning, an assembly of superconducting vortices exhibits a disordered hyperuniform structure when the vortex-vortex interactions are sufficiently strong, while when the quenched disorder dominates all other energy scales, a Poisson random arrangement of vortices appears [70]. One possibility is that the plastic flow phase of the skyrmions is Poisson random while the moving liquid phase has a disordered hyperuniform structure. In Fig. 6(e,f) we plot the skyrmion positions and S(k) for the moving crystal phase at F_D = 1.75, where the skyrmions have strong triangular ordering and S(k) shows sharp sixfold peaks.

Nonlinear velocity-force curves

Figure 7: (a) 〈V_||〉 and (b) 〈V_⊥〉, the average skyrmion velocity parallel and perpendicular to the drive, respectively, vs F_D for the system in Fig. 5 with n_sk=0.16, n_p=0.2, and α_m/α_d=9.95 at F_p = 0.5. Each curve has different nonlinear behavior near the depinning threshold. (c) The corresponding velocity deviations δV_|| (blue) and δV_⊥ (red) vs F_D, showing the strong fluctuations in the plastic flow regime. The letters a, c, and e in panel (c) indicate the values of F_D at which the images in Fig. 6 were obtained. Vertical dashed lines indicate the separations between the pinned phase, the plastic flow or phase segregated (PL-PS) state, the moving liquid (ML), and the moving crystal (MC).

In Fig. 7(a,b) we plot 〈V_||〉 and 〈V_⊥〉 versus F_D for the system in Fig. 5 at F_p = 0.5. Here we find a pinned phase for F_D < 0.08, a plastic flow or phase segregated (PL-PS) phase for 0.08 ≤ F_D < 0.425, a moving liquid (ML) phase for 0.425 ≤ F_D < 1.4, and a moving crystal (MC) phase for F_D ≥ 1.4. In the pinned phase, 〈V_||〉 = 〈V_⊥〉 = 0, and only small shifts in the particle positions occur as F_D is increased. In the plastic flow or partially phase separated state, 〈V_||〉 remains nearly constant while the magnitude of 〈V_⊥〉 increases linearly with increasing F_D. A cusp in 〈V_||〉 appears at the transition from plastic flow to the moving liquid phase, above which 〈V_||〉 begins to increase linearly with F_D. There is little change in the behavior of 〈V_⊥〉 through the PL-PS, ML, and MC phases, nor does any signature of the transition from the ML to the MC phase appear in 〈V_||〉. In Fig. 7(c) we plot the velocity deviations δV_|| and δV_⊥ versus F_D. In the PL phase, these velocity fluctuations are largest in the perpendicular direction, while in the ML and MC phases, the fluctuations are reduced and become mostly isotropic. These results show that the strong nonlinearity of the velocity-force curves at lower drives has a very different character than that found for overdamped particles such as superconducting vortices that exhibit plastic depinning, where 〈V_||〉 increases monotonically with F_D according to 〈V_||〉 ∝ (F_D −F_c)^β with β ≈ 1.5 [1,2]. No such scaling can be applied to the 〈V_||〉 vs F_D curve in the skyrmion system, while the 〈V_⊥〉 curve has β = 1.0. Clearly the Magnus force strongly modifies the scaling of the velocity-force curves. It has been argued that non-dissipative effects can change the nature of the depinning transition from continuous to discontinuous when inertia or stress overshoots are included [1,71]. In our system, we find that the 〈V_||〉 versus F_D curves begin to develop a discontinuous jump at depinning when the Magnus term is finite.

Figure 8: Dynamic phase diagram as a function of F_D vs F_p for the system in Figs. 1 to 7 with n_sk=0.16, n_p=0.2, and α_m/α_d=9.95, highlighting the pinned crystal phase which depins elastically into a moving crystal phase, the pinned skyrmion glass phase, the plastic flow phase, and the moving liquid phase.

By conducting a series of simulations for varied F_p and analyzing features in the velocity-force and P₆ curves, we construct the dynamic phase diagram as a function of F_D versus F_p shown in Fig. 8. The pinned crystal phase depins elastically into a moving crystal phase. In contrast, the pinned skyrmion glass phase depins into a plastic flow phase, which transitions into a moving crystal phase for lower F_p or a moving liquid for higher F_p. The moving liquid phase transitions into a moving crystal at higher drives. For F_p > 0.3, we find an increasing amount of clustering occurring in the plastic flow phase. Overall the phase diagram is similar to that found in overdamped systems, except that in the latter, the moving crystal phase is replaced by a moving smectic phase since the dynamically generated fluctuations experienced by the particles are highly anisotropic. In the skyrmion system, the Magnus force mixes the fluctuations in the driving direction into the transverse direction, giving more isotropic fluctuations that cause the particles to reorder into a moving crystal rather than a moving smectic state. The isotropy of the fluctuations increases as the Magnus force increases, as studied in detail in previous work [65].

IV. DYNAMICS AS A FUNCTION OF SKYRMION DENSITY

Figure 9: (a) F_c vs n_sk for samples with n_p=0.2, F_p = 0.02, and α_m/α_d = 9.95. (b) The corresponding P₆ vs n_sk. The transition from elastic to plastic depinning occurs near n_sk = 0.125. For n_sk < 0.02, the behavior of the system is in the single skyrmion limit. (c,d) Zoomed in plots of panels (a) and (b), respectively, for the region near n_sk=0.125 where the transition from elastic to plastic depinning occurs. A drop in P₆ is correlated with an increase in F_c, which is similar to the peak effect phenomenon.

We next consider the effect of varying the skyrmion density while holding the pinning density and pinning strength fixed. Such a situation could be achieved experimentally by varying the magnetic field. In Fig. 9(a,b) we plot F_c versus n_sk for samples with n_p=0.2, F_p = 0.02, and α_m/α_d = 9.95. An elastic solid with triangular ordering forms when n_sk ≥ 0.125, where we find P₆ = 1.0 and low F_c. For 0.02 ≤ n_sk < 0.125, we observe a pinned skyrmion glass that depins plastically, as indicated by the increase in F_c and the drop in P₆. For n_sk < 0.02, the distance between neighboring skyrmions becomes so great that the system enters the limit of non-interacting skyrmions, in which F_c ≈ F_p and the skyrmions are better described as a pinned gas. Figure 9(c,d) shows a blowup of Fig. 9(a,b) near n_sk=0.125 where the transition from elastic to plastic depinning occurs. There is a clear increase in F_c at the transition produced when topological defects appear in the system and P₆ drops below 1. The transition to plastic depinning with decreasing skyrmion density occurs due to the corresponding decrease in the shear modulus of the skyrmion lattice. Once the shear modulus becomes small enough, topological defects percolate within the lattice, producing a field-induced peak effect phenomenon.

Transverse locking in the elastic depinning regime

In the elastic depinning regime, the skyrmions depin as a unit and maintain their triangular lattice ordering. The moving lattice can become oriented in the direction of drive or may remain oriented in some particular direction due to the geometry of the sample. In some cases, it may be necessary for topological defects to nucleate inside the lattice in order to permit it to rotate and orient with the driving direction, and since these defects are energetically costly, the lattice orientation may remain fixed in the moving state even when the drive, and the effective skyrmion Hall angle, increase.

Le Doussal and Giamarchi argued that a moving superconducting vortex lattice interacting with pinning and subjected to a longitudinal drive F^||_D can exhibit a finite threshold for transverse depinning when an additional drive F^⊥_D is applied perpendicular to the longitudinal drive, and that the lattice can begin sliding along the transverse direction as well as the longitudinal direction when F^⊥_D is large enough [34]. This transverse critical force has been observed in simulations of moving superconducting vortices [36,72,73,74,75] and Wigner crystals [18,74] as well as in superconducting vortex experiments [76,77]. Le Doussal and Giamarchi also predicted that if the system forms a moving triangular lattice which remains oriented in a particular direction, then under an additional transverse drive, the initial transverse depinning threshold is followed by a series of higher-order transverse depinning thresholds that appear whenever the vector of net applied force aligns with a symmetry direction of the moving triangular lattice. Such directional locking effects were observed in simulations of triangular vortex lattices moving over random substrates under a fixed longitudinal drive and an increasing transverse drive [74], and similar effects were demonstrated for particles moving over periodic [78,79,80] and quasiperiodic substrates [82,83] .

Figure 10: The system from Fig. 9 with n_p=0.2, F_p=0.02, and α_m/α_d=9.95 in the elastic regime at n_sk = 0.207. (a) 〈V_||〉 vs F_D. (b) R = 〈V_⊥〉/〈V_||〉 vs F_D. (c) θ_sk = tan⁻¹(R) vs F_D. There is a series of steps on which the skyrmion lattice motion locks to specific skyrmion Hall angles of θ_sk = 60^°, 74^° and 79.2^°, corresponding to the alignment of the direction of motion with a symmetry direction of the skyrmion lattice.

In the skyrmion case, we find that transverse directional locking arises in the elastic flow regime in the absence of any additional transverse applied force, which does not occur in the overdamped limit. The directional locking of the skyrmion lattice is a result of the velocity dependence of the skyrmion Hall angle, which causes the net direction of motion of the skyrmion lattice to change as the velocity increases. When the direction of motion aligns with a symmetry direction of the skyrmion lattice, we find a locking effect, as shown in Fig. 10 for the system in Fig. 9 in the elastic regime with n_sk = 0.207. In Fig. 10(a) we plot 〈V_||〉 versus F_D where we observe three step features. The R=〈V_⊥〉/〈V_||〉 versus F_D curve in Fig. 10(b) shows more clearly that along these steps, R is constant, while in the plot of θ_sk versus F_D in Fig. 10(c), the steps correspond to skyrmion Hall angles of 60^°, 74^°, and 79.2^°. In each case the skyrmion lattice remains locked to a specific skyrmion Hall angle over a fixed interval of F_D. For a triangular lattice, the locking occurs when θ_sk = tan⁻¹(√3 p/(2q +1)), where p and q are integers. At p = 1 and q = 0, θ_sk=60^°; at p = 2 and q = 0, θ_sk=74^°; and at p = 3 and q = 0, θ_sk=79.2^°. Some smaller steps appear for higher values of q.

Figure 11: A blowup of the θ_sk = 79.2^° locking step in Fig. 10. (a) 〈V_||〉 vs F_D has a linear increase along the locking step. (b) R vs F_D and (c) θ_sk vs F_D both have shapes on either end of the locking step that are consistent with what is expected in phase locking systems.

In Fig. 11 we show a blowup of the curves in Fig. 10 on the p = 2, q = 0 step at θ_sk=79.2^°. Here 〈V_||〉 increases along the step while R remains flat and on either side of the step has the shape expected for a phase locked system such as a Shapiro step. Figure 11(c) shows that θ_sk is locked to a fixed angle as well. We find that the dynamical fluctuations are generally reduced on each step and that the peaks in S(k) are sharper, similar to the enhanced ordering in step regions observed in other systems that exhibit phase locking. These results show that an elastic skyrmion lattice exhibits a self-induced phase locking that has the same features as phase locking in an overdamped system but that occurs under the application of a single fixed direction dc drive rather than two superimposed dc drives or one rotating dc drive. In the plastic depinning regime, the dynamically reordered skyrmion lattices that appear at high drives generally still contain a small number of topological defects, which smear out the directional locking features.

Figure 12: 〈V_||〉 vs F_D for the system in Fig. 9 with n_p=0.2, F_p=0.02, and α_m/α_d=9.95. At n_sk = 0.01 (dark blue), the depinning threshold F_c is close to the single particle limit and the system does not dynamically order. At n_sk = 0.15 (light blue), the depinning is plastic, F_c is higher than in the elastic limit, and a plateau appears in the velocity response. At n_sk = 0.2 (red), the depinning is elastic. The dashed line indicates the velocity response in the pin-free limit, showing that the introduction of pinning actually increases 〈V_||〉 due to a speed up effect.

In Fig. 12 we plot 〈V_||〉 versus F_D for the system in Fig. 9 for varied skyrmion density. At a low density of n_sk = 0.01, the system is in the single skyrmion limit where the critical depinning force F_c is high and the skyrmions do not dynamically order. Here we find a sharp depinning threshold followed by a monotonic increase in 〈V_||〉 with F_D. At n_sk = 0.15, the skyrmions depin plastically and dynamically reorder at higher drives. In this case, just above the depinning threshold we find a window in which 〈V_||〉 remains roughly constant with increasing F_D in the plastic flow regime before switching to a monotonic increase in the dynamically reordered regime. For a higher density of n_sk = 0.2, F_c is small, the skyrmions depin elastically, and 〈V_||〉 increases monotonically with F_D. In the plastic flow window of the n_sk=0.15 sample just above depinning, where only some of the skyrmions have depinned and are moving while the rest remain pinned, 〈V_||〉 is larger than the value found over the same range of drives for the elastically flowing n_sk=0.2 sample, even though in the denser sample, all of the skyrmions are moving. The two velocity-force curves cross near F_D = 0.175, above which 〈V_||〉 is higher for the denser elastically flowing system. At higher values of F_D, 〈V_||〉 converges to the pin-free value (shown as a dashed line) for all values of n_sk. Over a large region of drive, extending from the depinning transition to F_D=0.04 and higher, we find a pinning-induced speed up effect in which the skyrmions move faster in the direction of the applied drive than a freely moving overdamped particle, as indicated by the fact that the velocity-force curves fall above the dashed line. The pinning-induced speed up effect results when the interaction of the skyrmion with the pinning site is partially transformed into motion along the driving direction by the Magnus force. Such effects have been observed previously in simulations with periodic pinning or line like defects. For higher drives, the skyrmions move faster, the effectiveness of the pinning is reduced, and 〈V_||〉 gradually approaches its pin-free value. If the relative strength α_m/α_d of the Magnus term is lowered, the size of the speed up effect diminishes, and in the damping-dominated limit, 〈V_||〉 is always equal to or less than the pin-free value. These results show that speed up effects for skyrmions persist even when the disorder is random rather than periodic.

Figure 13: Dynamic phase diagram as a function of F_D vs n_sk for the system in Figs. 9 to 12 with n_p=0.2, F_p = 0.02 and α_m/α_d=9.95 highlighting the pinned glass, pinned crystal, plastic flow, moving liquid, and moving crystal phases.

By conducting a seres of simulations, we construct a dynamic phase diagram as a function of F_D versus skyrmion density n_sk, as shown in Fig. 13. For n_sk < 0.125, the system forms a pinned glass, and it may be possible to further distinguish the formation of a pinned gas phase for n_sk < 0.02 where the system enters the single skyrmion limit. For n_sk ≥ 0.125, the pinned crystal depins into a moving crystal, while for 0.02 < n_sk < 0.125, the pinned glass undergoes plastic depinning into a plastic flow phase which transitions into a moving liquid and finally into a moving crystal at high drives. For n_sk < 0.02, above depinning the system always remains in a moving liquid phase and dynamical reordering never occurs.

V. DYNAMICS AS A FUNCTION OF MAGNUS FORCE

Figure 14: (a) 〈V_||〉 vs F_D and (b) δV_|| (blue) and δV_⊥ (red) vs F_D for a sample with F_p = 0.2, n_sk = 0.16, and n_p = 0.2 in the overdamped limit of α_m/α_d = 0. (c) 〈V_||〉 vs F_D and (d) δV_|| (blue) and δV_⊥ (red) vs F_D for a sample with the same parameters except with α_m/α_d = 1.0.

In Fig. 14(a,b) we plot 〈V_||〉, δV_||, and δV_⊥ versus F_D for a system with F_p = 0.2, n_sk = 0.16, and n_p = 0.2 in the overdamped limit of α_m/α_d = 0. Under these conditions, 〈V_⊥〉 = 0, and the initial increase in 〈V_||〉 with F_D just above depinning has the nonlinear form 〈V_||〉 ∝ (F_D − F_C)^β with β ≈ 1.3 to 1.5, as previously observed for plastic depinning in vortex matter [1,30]. At higher drives F_D > 0.2 where all the skyrmions are moving, the velocity-force curve becomes linear. We find that in this overdamped system, δV_|| > δV_⊥ for all drives since the fluctuating force generated by the pinning sites is aligned with the driving direction. The strongly anisotropic pinning-induced fluctuation forces cause the system to form a moving smectic, as predicted from theory [33,34] and observed in previous simulations [1,36,37,65] and experiments [35]. In Fig. 14(c,d), we plot 〈V_||〉, δV_||, and δV_⊥ versus F_D in a system with the same parameters except with α_m/α_d = 1.0. Here, the onset of linear behavior in the velocity-force curve shifts closer to the depinning transition, while δV_|| > δV_⊥ only in the strongly plastic flow region F_c ≤ F_D ≤ 0.1. Within the plastic flow regime, θ_sk is zero at depinning and slowly increases toward the intrinsic value θ_sk^int with increasing F_D. For F_D > 0.1 in the moving crystal phase, we find δV_⊥ > δV_||. The crossover in the magnitude of the velocity fluctuations occurs because the Magnus force induces fluctuations that are perpendicular to the forces exerted by the pinning sites. At higher drives, δV_||/δV_⊥ → 1.0 as the effectiveness of the pinning is reduced.

Figure 15: (a) 〈V_||〉 vs F_D and (b) δV_|| (blue) and δV_|| (red) vs F_D for the system in Fig. 14 with F_p=0.2, n_sk=0.16, and n_p=0.2 at α_m/α_d = 4.0. (c) 〈V_||〉 vs F_D and (d) δV_|| (blue) and δV_⊥ (red) vs F_D for the same system at α_m/α_d = 15.79, where we find a region in which 〈V_||〉 decreases with increasing F_D, indicative of negative differential conductivity.

In Fig. 15(a,b) we plot 〈V_||〉, δV_||, and δV_⊥ for the system in Fig. 14 at α_m/α_d = 4.0. Here the velocity-force curve develops a plateau above depinning, destroying the scaling associated with plastic flow in the overdamped limit. For F_c < F_D < F_p = 0.2, moving and pinned skyrmions coexist, and we find strongly pronounced velocity fluctuations with δV_⊥ > δV_||. The velocity-force curves become linear for F_D > 0.2; however, dynamical reordering does not occur until a much higher F_D, and the system is in a moving liquid phase. In Fig. 15(c,d) we show 〈V_||〉, δV_||, and δV_⊥ versus F_D for a sample with the same parameters but at α_m/α_d = 15.79. Here, there is a region in which 〈V_||〉 decreases with increasing F_D, indicative of negative differential conductivity. For F_D > F_p = 0.2, 〈V_||〉 increases linearly with F_D, while δV_|| and δV_⊥ are largest for F_c < F_D < 0.19. In general, we find that increasing either the Magnus force or F_p increases the range over which 〈V_||〉 is flat or decreasing with increasing F_D, with the maximum range corresponding to F_c < F_D < F_p. Negative differential conductivity, d〈V_||〉/dF_D < 0, appears for sufficiently large Magnus force in the regime containing a combination of moving and pinned skyrmions, and occurs when the increase in F_D combined with the Magnus force generates an increasing velocity component in the direction perpendicular to the drive due to collisions between moving and pinned skyrmions, lowering the velocity response parallel to the drive. For F_D > F_p, all the skyrmions depin and the negative differential conductivity is lost.

Figure 16: Dynamic phase diagram as a function of F_D vs α_m/α_d for the system in Figs. 14 and 15 with F_p = 0.2, n_sk = 0.16 and n_p = 0.2, highlighting the pinned, plastic, moving liquid, and moving crystal phases. For α_m/α_d = 0, the moving crystal phase is replaced by a moving smectic state. The depinning threshold F_c decreases with increasing α_m/α_d.

By conducting a series of simulations and examining the nonlinear features in the velocity-force and P₆ versus F_D curves, we can construct a dynamical phase diagram as a function of F_D versus α_m/α_d, as shown in Fig. 16. At α_m/α_d = 0, the pinned and plastic flow phases are followed at higher F_D by dynamical reordering into a moving smectic state, as described in detail in Ref. [65]. For 0 < α_m/α_d < 6.5, the system dynamically orders into a moving crystal phase when F_d ≈ F_p. For α_m/α_d > 7.5, we find a growing window of a moving liquid state in which all of the skyrmions are moving but there is still considerable topological disorder. The moving liquid regime increases in extent with larger α_m/α_d due to the rotational character of the fluctuations generated by the Magnus force. If α_m/α_d is sufficiently large, the Magnus force enhances the net force experienced by the skyrmions when F_D/F_p > 1.0, and the resulting fluctuations melt the skyrmion lattice. The magnitude of the fluctuations grows roughly linearly with α_m/α_d, while the magnitude of the forces exerted by the pinning sites decrease as 1/F_D [1], so the value of F_D at which dynamical reordering into the moving crystal phase occurs increases roughly linearly with α_m/α_d. For the illustrated value of F_p, the velocity-force curves develop a window in the plastic flow regime in which 〈V_||〉 remains constant or decreases with increasing F_D. We note that it is possible for the smectic phase observed at α_m/α_d=0 to persist for finite but small values of α_m/α_d, as will be discussed elsewhere. The value of F_c marking the depinning transition into the plastic flow state shifts to lower F_D with increasing α_m/α_d as also found in previous simulations, and it has been argued that the Magnus force is one of the reasons that the critical depinning force is small in skyrmion systems [49].

VI. DENSITY PHASE SEPARATION AND DYNAMIC PHASE SEPARATION

When both the pinning and the Magnus force are strong, we observe a dynamically induced density segregation or skyrmion clustering effect. This effect was first found in continuum-based simulations of moving skyrmions in the strong substrate limit, where it was attributed to an attraction between the skyrmions arising from spin wave excitations generated by the fluctuating internal modes of the skyrmions [67]. Recent simulations with periodic pinning arrays show that a strong clustering effect occurs for moving skyrmions when both the Magnus force and the pinning strength are sufficiently large [84]. In these simulations, which contain no spin waves, the effect was attributed to the drive dependence of the skyrmion Hall angle, which causes different regions of the skyrmions to move toward each other due to their differing values of θ_sk if a sufficiently strong velocity gradient can be induced by the pinning. In the case of periodic pinning, this situation arises both in the plastic flow regime and at higher drives. Here we show that a similar dynamical density phase separation can occur for strong random pinning, but that it is restricted to the regime F_D/F_p < 1.0. We also find two possible types of phase separation: a density modulated state for strong pinning, and bands of moving skyrmions coexisting with bands of pinned skyrmions for weaker pinning.

Figure 17: Skyrmion positions for a system with F_p = 1.5, n_sk = 0.44, n_p = 0.6, and α_m/α_d = 10. (a) The pinned phase at F_D = 0.2 has a uniform skyrmion density. (b) The density phase separated state at F_D = 0.6. (c) The transition from the density phase separated state to the moving liquid state at F_D = 1.25. (d) The moving liquid phase at F_D=2.0 where the skyrmion density is uniform.

Figure 18: Skyrmion positions in the density segregated state for the system in Fig. 17 with n_sk=0.44, n_p=0.6, and α_m/α_d=10 at F_D/F_c = 0.6 for (a) F_p = 1.0, (b) F_p = 3.5, and (c) F_p = 5.0, showing that as the disorder strength increases, the skyrmion bands become narrower. (d) The F_p = 3.5 system at n_sk = 0.67, showing the persistence of the bands at higher skyrmion densities.

The density phase separation is most pronounced in denser systems, as illustrated in Fig. 17 where we show the skyrmion positions at different drives for a system with n_sk = 0.44, n_p = 0.6, α_m/α_d = 10, and F_p = 1.5. In Fig. 17(a) at F_D = 0.2, we find a uniform disordered pinned glass state, while at F_D = 0.6 in the plastic flow state, Fig. 17(b) shows that a dense band of skyrmions emerges that is surrounded by a region of low skyrmion density. At F_D = 1.25 in Fig. 17(c), near the transition from the density phase separated state to the moving liquid, the density banding is reduced, while in the moving liquid phase at F_D = 2.0 in Fig. 17(d), the density phase separation is lost and the skyrmion density becomes uniform. In general, the density phase separation occurs when F_p > 0.5, n_p > 0.3, α_m/α_d > 5.0, and F_D/F_p < 1.0, in a regime where there is a combination of moving and pinned skyrmions. The density phase separation takes the form of bands of skyrmions roughly aligned with the direction of motion θ_sk, similar to what was observed in the continuum-based simulation studies. In Fig. 18(a) we show the skyrmion positions for F_D/F_p = 0.6 in the system from Fig. 17 at F_p = 1.0, where we find that the bands of skyrmions are wider but still present. At the same value of F_D/F_c for F_p=3.5 and 5.0, as shown in Figs. 18(b, c), respectively, we observe a compression of the skyrmion bands as F_p increases. Figure 18(d) illustrates the F_p = 0.35 system at a higher skyrmion density of 0.67, showing that the banding persists for higher skyrmion densities.

Figure 19: (a) Skyrmion positions (dots) and trajectories (lines) for the system in Fig. 17 with n_sk=0.44, n_p=0.6, and α_m/α_d=10 at F_p = 0.3 and F_D=0.1 where the density phase segregation is lost but a dynamical segregation emerges in which the motion is confined to a band. (b) An image of only the skyrmion positions from panel (a) showing that the skyrmion density is uniform.

For the parameters illustrated in Figs. 17 and 18, we find that when 0.1 < F_p < 0.3, the density phase separation disappears and is replaced by a dynamical phase segregation in which the density is uniform but the motion occurs only in localized bands. This is shown in Fig. 19(a) where we plot the skyrmion trajectories over a period of time in a sample with F_p=0.3 at constant F_D = 0.1. Here a wide band of moving skyrmions coexists with a pinned band. Figure 19(b) shows only the particle positions from Fig. 19(a) where it is clear that the skyrmion density is uniform. For the same parameter set at 0.05 < F_p ≤ 0.1, we find a uniform plastic flow phase, and for F_p < 0.05, the depinning is elastic.

Figure 20: Dynamic phase diagram as a function of F_D vs F_p for the system in Figs. 17 to 19 with n_sk = 0.44, n_p = 0.6, and α_m/α_d = 10 showing the pinned crystal (PC), the pinned glass (PG), the dynamically phase separated state (DPS) illustrated in Fig. 19, the density phase separated state (PS) illustrated in Figs. 17 and 18, the moving liquid (ML), and the moving crystal (MC).

Figure 21: Dynamic phase digram as a function of F_D vs α_m/α_d for the system in Figs. 17 to 20 with F_p = 1.5, n_sk = 0.44, and n_p = 0.6 showing the pinned state, dynamically phase separated state (DPS), density phase separated state (PS), moving liquid (ML), and moving crystal (MC). The PS state appears only for α_m/α_d > 5.0.

Figure 22: Skyrmion positions (dots) and trajectories (lines) for the system in Fig. 21 with F_p=1.5, n_sk=0.44, and n_p=0.6 at α_m/α_b = 15. (a) At F_D = 0.3, multiple bands appear consisting of both moving and pinned skyrmions. (b) At F_D = 1.2, the bands make a steeper angle with the applied drive, and kinks appear as the bands rotate to match the skyrmion Hall angle, which increases with increasing F_D.

In Fig. 20 we plot a dynamical phase diagram as a function of F_D versus F_p for the system in Figs. 17 to 19. For F_p < 0.05, a pinned crystal (PC) phase appears which depins directly into the moving crystal (MC) phase. In the moving liquid (ML) phase, the system is disordered but there is no dynamical or density phase separation. The dynamically phase separated state (DPS), illustrated in Fig. 19, has uniform skyrmion density but phase separated moving regions, while the density phase separated state (PS), illustrated in Figs. 17 and 18, has nonuniform skyrmion density. We find a pinned glass region (PG) at low F_D when F_p is sufficiently large. In Fig. 21 we show the dynamical phase diagram as a function of F_D versus α_m/α_d for the same system at fixed F_p = 1.5. The PS phase appears only when α_m/α_d > 5.0, while the DPS phase extends from 1.5 < α_m/α_d ≤ 5.0. At α_m/α_d = 0, the MC phase is replaced by a moving smectic phase (not shown). When α_m/α_d > 10, we find that the bands in the PS phase sharpen and split into multiple lanes, as illustrated in Fig. 22(a) at α_m/α_d = 15 and F_D = 0.3. Here, multiple bands appear that are each composed of both moving and pinned skyrmions. As F_D is increased, the bands simultaneously widen and move at a steeper angle with respect to the applied drive, since the skyrmion Hall angle increases with increasing drive. The rotation of the bands as they follow the skyrmion Hall angle generally occurs via the formation of kinks, in which one portion of the band is moving at the lower angle while another portion is moving at the new, higher angle, as shown in Fig. 22(b) at a higher F_D = 1.2.

Figure 23: Dynamic phase diagram as a function of F_D vs n_p for a system with n_sk = 0.44, F_p = 10, and α_m/α_d = 10 showing the pinned, plastic flow (PF), dynamically phase separated (DPS), phase separated (PS), moving liquid (ML), and moving crystal (MC) states. In the PF phase, there is a combination of pinned and flowing skyrmions but there is no dynamical or density phase separation. The DPS and PS states appear only when the disorder is sufficiently dense and strong.

In Fig. 23 we plot a dynamic phase diagram as a function of F_D versus n_p for samples with n_sk = 0.44, α_m/α_d=10, and F_p = 1.5. We observe the PS phase when n_p > 0.3 and the DPS phase in the range 0.1 < n_p ≤ 0.3. The skyrmion density remains uniform when n_p < 0.1 and/or F_D < F_p, but in this regime we can distinguish between a plastic flow (PF) phase in which moving and pinned skyrmions coexist, and a ML phase in which all the skyrmions are moving but the system is disordered. The transition to the MC phase shifts to higher values of F_D with increasing n_p, while the transition into the ML phase remains roughly constant with increasing n_p since it is controlled by the value of F_p.

The dynamic phase diagrams in Figs. 20, 21, and 22 indicate that a moving segregated state can arise in particle-based skyrmion models when both the pinning and the Magnus force are sufficiently strong. We note that our particle-based model does not include the generation of spin waves by the moving skyrmions, which was the mechanism proposed to be responsible for the clustering transition observed in continuum simulations. The clustering transition we observe arises due to the velocity differential exhibited by the skyrmions as they move over the strong random pinning. The pinned or slowly moving skyrmions have a smaller skyrmion Hall angle than the more rapidly moving skyrmions, and as a result, these two types of skyrmions tend to move toward each other. It is not clear whether the clustering effect we observe is actually the same as that found in the continuum simulations [67] or whether skyrmion cluster states can be generated via more than one mechanism. Recent experiments involving nonequilibrium quenches of a skyrmion system also show the formation of clustered or phase separated states [86], so it is possible that density segregated states are a general phenomenon in nonequilibrium skyrmion systems.

VII. DISCUSSION

Our results should be general to other particle-based systems driven over random disorder where a Magnus force is present, such as certain type-II superconducting vortices, colloidal particles with an additional rotational degree of freedom, and charged particles in a magnetic field. Although our work was motivated by skyrmion dynamics, there are limitations when using a rigid model to represent the skyrmion motion. It is possible for the skyrmions to undergo significant shape distortions in the presence of strong disorder or strong driving, and in some cases the quenched disorder can lead to the creation and annihilation of skyrmions [60,67]. Shape distortions could modify the forces experienced by the skyrmions, such as by enhancing the skyrmion Hall angle as proposed in Ref. [54], increasing the amount of damping, or creating effective inertial terms [87,88,89,90]. Such behaviors are not captured in our particle-based model. We emphasize that it is important to obtain an understanding of the behavior of the rigid model in the presence of disorder before introducing additional features to the model or even before performing much more computationally expensive micromagnetic simulations.

Possible improvements to the particle-based model that could capture some of the effects listed above include mimicking the effects of skyrmion distortions by the addition of an inertial term such as mdv/dt, representing the effective mass induced by the shape changes [87]. This mass could be positive or negative depending on the type of distortions or whether the skyrmion is radiating magnons. It is known that internal modes can arise in moving skyrmions [91], and that skyrmion motion can be generated by the internal modes even in the absence of pinning [92,93,94]. The internal modes can cause the skyrmion to expand or shrink repeatedly, and as a result the damping experienced by the skyrmion can become frequency or drive dependent. Inclusion of an inertial term or a variable damping term for the skyrmion motion could potentially produce a wide range of additional features in the transport curves, such as jumps, dips, or a negative differential conductivity similar to a Walker breakdown. Moving skyrmions can also radiate magnons, which can modify the skyrmion-skyrmion interaction potential and produce an effective attractive or aligning interaction [95], leading to the formation of dynamic skyrmion chain states or moving smectics. Magnon dynamics could be modeled by adding an attractive term along with a drive dependence to the pairwise skyrmion interactions.

In this work we focus on relatively short range pinning potentials; however, it is possible for disorder to occur at much larger wavelengths, as in the case of grain boundaries or line-like defects. It is known from studies of superconducting vortex systems that correlated disorder can produce different kinds of dynamics than random disorder [96] . Thermal disorder can also be important, as it is now understood that there are many cases in which Brownian motion of the skyrmions can arise even in the absence of disorder [88,97]. Although thermal effects are relatively unexplored, a recent study has shown that in the creep regime, the skyrmion Hall angle can depend strongly on the drive [98]. Additionally, it is possible for different types of skyrmions to appear, such as antiferromagnetic skyrmions [99,100] or an antiskyrmion lattice [101], and in such a situation, the dynamics could depend critically on the angle at which the driving force is applied. Multiple species of skyrmions could coexist in a single sample due to size effects or varied local properties [102,103,104]. This implies that a rich variety of dynamics could be realized in skyrmion systems that may be absent in other systems where only a single particle species is present.

VIII. SUMMARY

Using a particle-based model, we examine the various types of collective dynamic phases that can occur for skyrmions moving over random pinning under a dc drive as we vary the Magnus force, pinning strength, skyrmion density, and pinning density. For weak pinning, the skyrmions form a triangular lattice that depins elastically, and although there is no proliferation of topological defects at the elastic depinning transition, we find that the sixfold peaks in the structure factor diminish in weight due to smearing of the skyrmion positions near depinning, while the peaks sharpen again at higher drives when the skyrmion lattice becomes more ordered. As a function of increasing pinning strength or decreasing skyrmion density, we find a transition into a pinned skyrmion glass phase that depins plastically into a disordered moving state. This transition is accompanied by a sharp increase in the critical depinning force which resembles the peak effect phenomenon found in superconducting vortex systems at the transition from elastic to plastic depinning.

We find that the skyrmion Hall angle is zero at very low drives and increases with increasing driving force before saturating to the intrinsic value at high drives. In the elastic depinning regime for weak pinning, a directional locking effect occurs in which the direction of skyrmion motion locks to a symmetry direction of the triangular pinning substrate. As the drive increases, the skyrmion Hall angle also increases, producing a series of directional locking phases. These directional locking effects are similar to those predicted by Le Doussal and Giamarchi for elastic vortex lattices moving under a longitudinal drive that are subjected to an additional transverse applied driving force; however, in the skyrmion case, the direction of the net driving force remains fixed and the skyrmion Hall angle changes due to interactions with the pinning sites. We show that the skyrmion velocity-force curves differ substantially from those found in overdamped systems with random pinning, and that when the Magnus force is strong, there can be a plateau or even a decrease in the skyrmion velocity with increasing driving force, leading to negative differential conductivity. The scaling of the velocity-force curves changes under strong Magnus force from the typical form V = (F_D −F_c)^β observed in overdamped systems to a more discontinuous behavior similar to that predicted by Schwartz and Fisher for depinning in systems that include non-dissipative effects such as stress overshoots or inertia. As the Magnus force increases, we find a region of what we call a moving liquid phase in which the skyrmions are all in motion but the non-dissipative fluctuations induced by the skyrmion-pin interactions are large enough to disorder the skyrmion lattice. Under the same conditions in the overdamped limit, a moving smectic state appears instead.

One of the most striking features we observe is a density segregation or skyrmion clustering effect that occurs for strong pinning and strong Magnus force. Here the skyrmions form dense bands aligned with the driving direction that are separated by low density regions, a behavior similar to that recently found in continuum-based simulations in the strong random substrate limit as well as in particle-based simulations of skyrmions driven over periodic pinning arrays. As the pinning becomes weaker, we find that the density phase segregated state transitions into a dynamically phase separated state in which the skyrmion density is uniform but localized bands of moving skyrmions coexist with bands of pinned skyrmions, while for very weak pinning or small Magnus force, both the skyrmion density and the skyrmion motion are uniform. The density segregation arises due to the velocity-dependent skyrmion Hall angle induced by the Magnus force. When the pinning is strong enough, the skyrmion velocity can develop a large local differential, causing different groups of skyrmions to move at different Hall angles until the groups collide to form a region of enhanced skyrmion density at the cost of a density depleted region. The clustering effects occur in the plastic flow regime where there is a combination of pinned and moving skyrmions. Our results show that a particle-based model that neglects spin waves is sufficient to capture such clustering effects; however, it is not clear whether the skyrmion clustering observed in continuum based simulations is produced by the same mechanism as the clustering found in the particle-based model.

ACKNOWLEDGMENTS

We gratefully acknowledge the support of the U.S. Department of Energy through the LANL/LDRD program for this work. This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396 and through the LANL/LDRD program.

REFERENCES

[1]: C. Reichhardt and C.J.O. Reichhardt, Depinning and nonequilibrium dynamic phases of particle assemblies driven over random and ordered substrates: A review, Rep. Prog. Phys. 80, 026501 (2017).
[2]: D. S. Fisher, Collective transport in random media: From superconductors to earthquakes, Phys. Rep. 301, 113 (1998).
[3]: S. Bhattacharya and M. J. Higgins, Dynamics of a disordered flux line lattice, Phys. Rev. Lett. 70, 2617 (1993).
[4]: G. Blatter, M. V. Feigel'man, V. B. Geshkenbein, A. I. Larkin, and V. M. Vinokur, Vortices in high-temperature superconductors, Rev. Mod. Phys. 66, 1125 (1994).
[5]: A. E. Koshelev and V. M. Vinokur, Dynamic melting of the vortex lattice, Phys. Rev. Lett. 73, 3580 (1994).
[6]: G. Shaw, P. Mandal, S.S. Banerjee, A. Niazi, A.K. Rastogi, A.K. Sood, S. Ramakrishnan, and A.K. Grover Critical behavior at depinning of driven disordered vortex matter in 2H-NbS₂, Phys. Rev. B 85, 174517 (2012).
[7]: C. Reichhardt and C. J. Olson, Colloidal dynamics on disordered substrates, Phys. Rev. Lett. 89, 078301 (2002).
[8]: A. Pertsinidis and X. S. Ling, Statics and dynamics of 2D colloidal crystals in a random pinning potential, Phys. Rev. Lett. 100, 028303 (2008).
[9]: A. Sengupta, S. Sengupta, and G.I. Menon, Driven disordered polymorphic solids: Phases and phase transitions, dynamical coexistence and peak effect anomalies, Phys. Rev. B 81, 144521 (2010).
[10]: P. Tierno, Depinning and collective dynamics of magnetically driven colloidal monolayers, Phys. Rev. Lett. 109, 198304 (2012).
[11]: S. Deutschländer, T. Horn, H. Löwen, G. Maret, and P. Keim, Two-dimensional melting under quenched disorder, Phys. Rev. Lett. 111, 098301 (2013).
[12]: C. Reichhardt, C.J.O. Reichhardt, I. Martin, and A.R. Bishop, Dynamical ordering of driven stripe phases in quenched disorder, Phys. Rev. Lett. 90, 026401 (2003).
[13]: J.-X. Chen, J.-W. Mao, S. Thakur, J.-R. Xu, and F. Liu, Dynamical phase of driven colloidal systems with short-range attraction and long-range repulsion J. Chem. Phys. 135, 094504 (2011).
[14]: C.J.O. Reichhardt, C. Reichhardt, and A.R. Bishop, Anisotropic sliding dynamics, peak effect, and metastability in stripe systems, Phys. Rev. E 83, 041501 (2011).
[15]: H.J. Zhao, V.R. Misko, and F.M. Peeters, Dynamics of self-organized driven particles with competing range interaction, Phys. Rev. E 88 022914 (2013).
[16]: F.I.B. Williams, P.A. Wright, R.G. Clark, E.Y. Andrei, G. Deville, D.C. Glattli, O. Probst, B. Etienne, C. Dorin, C.T. Foxon, and J.J. Harris, Conduction threshold and pinning frequency of magnetically induced Wigner solid, Phys. Rev. Lett. 66, 3285 (1991).
[17]: M.-C. Cha and H.A. Fertig, Peak effect and the transition from elastic to plastic depinning, Phys. Rev. Lett. 80 3851 (1998).
[18]: C. Reichhardt, C.J. Olson, N. Grønbech-Jensen, and F. Nori, Moving Wigner glasses and smectics: dynamics of disordered Wigner crystals, Phys. Rev. Lett. 86, 4354 (2001).
[19]: X. Wang, H. Fu, L. Du, X. Liu, P. Wang, L.N. Pfeiffer, K.W. West, R.-R. Du, and X. Lin, Depinning transition of bubble phases in a high Landau level, Phys. Rev. B 91, 115301 (2015).
[20]: A. Morin, N. Desreumaux, J.-B. Caussin, and D. Bartolo, Distortion and destruction of colloidal flocks in disordered environments, Nat. Phys. 13, 63 (2017).
[21]: Cs. Sándor, A. Libál, C. Reichhardt, and C.J.O. Reichhardt, Dynamic phases of active matter systems with quenched disorder, Phys. Rev. E 95, 032606 (2017).
[22]: M.S. Tomassone and J. Krim, Fractal scaling behavior of water flow patterns on inhomogeneous surfaces, Phys. Rev. E 54, 6511 (1996).
[23]: Y.-G. Cao, J. Liu, and G.-Y. Fu, Depinning dynamics of fluid monolayer on a quenched substrate, Commun. Theor. Phys. 54, 893 (2010).
[24]: P. Aussillous, Z. Zou, E. Guazzelli, L. Yan, and M. Wyart, Scale-free channeling patterns near the onset of erosion of sheared granular beds, Proc. Natl. Acad. Sci. (USA) 113, 11788 (2016).
[25]: C.J.O. Reichhardt, E. Groopman, Z. Nussinov, and C. Reichhardt, Jamming in systems with quenched disorder, Phys. Rev. E 86, 061301 (2012).
[26]: A. Vanossi, N. Manini, M. Urbakh, S. Zapperi, and E. Tosatti, Modeling friction: From nanoscale to mesoscale, Rev. Mod. Phys. 85, 529 (2013).
[27]: M.-C. Miguel, A. Vespignani, M. Zaiser, and S. Zapperi, Dislocation jamming and Andrade creep, Phys. Rev. Lett 89, 165501 (2002).
[28]: C. Zhou, C. Reichhardt, C.J.O. Reichhardt, and I.J. Beyerlein, Dynamic phases, pinning, and pattern formation for driven dislocation assemblies, Sci. Rep. 5, 8000 (2015).
[29]: J.M. Carlson and J.S. Langer, Properties of earthquakes generated by fault dynamics, Phys. Rev. Lett. 62, 2632 (1989).
[30]: Y. Fily, E. Olive, N. Di Scala, and J.C. Soret, Critical behavior of plastic depinning of vortex lattices in two dimensions: Molecular dynamics simulations Phys. Rev. B 82, 134519 (2010).
[31]: N. Di Scala, E. Olive, Y. Lansac, Y. Fily, and J.C. Soret, The elastic depinning transition of vortex lattices in two dimensions, New J. Phys. 14, 123027 (2012).
[32]: P. Moretti and M.-C. Miguel, Irreversible flow of vortex matter: Polycrystal and amorphous phases, Phys. Rev. B 80, 224513 (2009).
[33]: L. Balents, M.C. Marchetti, and L. Radzihovsky, Nonequilibrium steady states of driven periodic media, Phys. Rev. B 57, 7705 (1998).
[34]: P. Le Doussal and T. Giamarchi, Moving glass theory of driven lattices with disorder, Phys. Rev. B 57, 11356 (1998).
[35]: F. Pardo, F. de la Cruz, P. L. Gammel, E. Bucher, and D. J. Bishop, Observation of smectic and moving-Bragg-glass phases in flowing vortex lattices, Nature (London) 396, 348 (1998).
[36]: K. Moon, R.T. Scalettar, and G.T. Zimányi, Dynamical phases of driven vortex systems, Phys. Rev. Lett. 77, 2778 (1996).
[37]: C. J. Olson, C. Reichhardt, and F. Nori, Nonequilibrium dynamic phase diagram for vortex lattices, Phys. Rev. Lett. 81, 3757 (1998).
[38]: S. Okuma, K. Kashiro, Y. Suzuki, and N. Kokubo, Order-disorder transition of vortex matter in a-Mo_xGe_1−x films probed by noise, Phys. Rev. B 77, 212505 (2008).
[39]: B. Bag, D.J. Sivananda, P. Mandal, S.S. Banerjee, A.K. Sood, and A.K. Grover, Vortex depinning as a nonequilibrium phase transition phenomenon: Scaling of current-voltage curves near the low and the high critical-current states in 2H-NbS₂ single crystals, Phys. Rev. B 97, 134510 (2018).
[40]: S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii, and P. Böni, Skyrmion lattice in a chiral magnet, Science 323, 915 (2009).
[41]: X. Z. Yu, Y. Onose, N. Kanazawa, J. H. Park, J. H. Han, Y. Matsui, N. Nagaosa, and Y. Tokura, Real-space observation of a two-dimensional skyrmion crystal, Nature (London) 465, 901 (2010).
[42]: W. Jiang, P. Upadhyaya, W. Zhang, G. Yu, M. B. Jungfleisch, F.Y. Fradin, J.E. Pearson, Y. Tserkovnyak, K.L. Wang, O. Heinonen, S.G.E. te Velthuis, and A. Hoffmann, Blowing magnetic skyrmion bubbles, Science 349, 283 (2015).
[43]: Y. Tokunaga, X.Z. Yu, J.S. White, H.M. Rønnow, D. Morikawa, Y. Taguchi, and Y. Tokura, A new class of chiral materials hosting magnetic skyrmions beyond room temperature, Nat. Commun. 6, 7638 (2015).
[44]: S. Woo, K. Litzius, B. Krüger, M.-Y. Im, L. Caretta, K. Richter, M. Mann, A. Krone, R.M.Reeve, M. Weigand, P. Agrawal, I. Lemesh, M.-A. Mawass, P. Fischer, M. Kläui, and G.S.D. Beach, Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets, Nat. Mater. 15, 501 (2016).
[45]: W. Legrand, D. Maccariello, N. Reyren, K. Garcia, C. Moutafis, C. Moreau-Luchaire, S. Collin, K. Bouzehouane, V. Cros, and A. Fert, Room-temperature current-induced generation and motion of sub-100 nm skyrmions, Nano Lett. 17, 2703 (2017).
[46]: A. Soumyanarayanan, M. Raju, A.L. Gonzalez-Oyarce, A.K.C. Tan, M.-Y. Im, A.P. Petrovic, P. Ho, K.H. Khoo, M. Tran, C.K. Gan, F. Ernult, and C. Panagopoulos, Tunable room-temperature magnetic skyrmions in Ir/Fe/Co/Pt multilayers, Nat. Mater. 16, 898 (2017).
[47]: R. Tolley, S.A. Montoya, and E.E. Fullerton, Room-temperature observation and current control of skyrmions in Pt/Co/Os/Pt thin films, Phys. Rev. Mater. 2, 044404 (2018).
[48]: T. Schulz, R. Ritz, A. Bauer, M. Halder, M. Wagner, C. Franz, C. Pfleiderer, K. Everschor, M. Garst, and A. Rosch, Emergent electrodynamics of skyrmions in a chiral magnet, Nat. Phys. 8, 301 (2012).
[49]: N. Nagaosa and Y. Tokura, Topological properties and dynamics of magnetic skyrmions, Nat. Nanotechnol. 8, 899 (2013).
[50]: J. Iwasaki, M. Mochizuki, and N. Nagaosa, Universal current-velocity relation of skyrmion motion in chiral magnets, Nat. Commun. 4, 1463 (2013).
[51]: D. Liang, J. P. DeGrave, M. J. Stolt, Y. Tokura, and S. Jin, Current-driven dynamics of skyrmions stabilized in MnSi nanowires revealed by topological Hall effect, Nat. Commun. 6, 8217 (2015).
[52]: X.Z. Yu, N. Kanazawa, W.Z. Zhang, T. Nagai, T. Hara, K. Kimoto, Y. Matsui, Y. Onose, and Y. Tokura, Skyrmion flow near room temperature in an ultralow current density, Nat. Commun. 3, 988 (2012).
[53]: W. Jiang, X. Zhang, G. Yu, W. Zhang, X. Wang, M.B. Jungfleisch, J.E. Pearson, X. Cheng, O. Heinonen, K.L. Wang, Y. Zhou, A. Hoffmann, and S.G.E. te Velthuis, Direct observation of the skyrmion Hall effect, Nat. Phys. 13, 162 (2017).
[54]: K. Litzius, I. Lemesh, B. Krüger, P. Bassirian, L. Caretta, K. Richter, F. Büttner, K. Sato, O.A. Tretiakov, J. Förster, R.M. Reeve, M. Weigand, I. Bykova, H. Stoll, G. Schütz, G.S.D. Beach, and M. Kläui, Skyrmion Hall effect revealed by direct time-resolved X-ray microscopy, Nat. Phys. 13, 170 (2017).
[55]: S. Woo, K.M. Song, X.C. Zhang, Y. Zhou, M. Ezawa, X.X. Liu, S. Finizio, J. Raabe, N.J. Lee, S.I. Kim, S.Y. Park, Y. Kim, J.Y. Kim, D. Lee, O. Lee, J.W. Choi, B.C. Min, H.C. Koo, and J. Chang, Current-driven dynamics and inhibition of the skyrmion Hall effect of ferrimagnetic skyrmions in GdFeCo films, Nat. Commun. 9, 959 (2018).
[56]: A. Fert, V. Cros, and J. Sampaio, Skyrmions on the track, Nat. Nanotechnol. 8, 152 (2013).
[57]: S.-Z. Lin, C. Reichhardt, C.D. Batista, and A. Saxena, Particle model for skyrmions in metallic chiral magnets: Dynamics, pinning, and creep, Phys. Rev. B 87, 214419 (2013).
[58]: C. Reichhardt, D. Ray, and C.J.O. Reichhardt, Collective transport properties of driven skyrmions with random disorder, Phys. Rev. Lett. 114, 217202 (2015).
[59]: J.-V. Kim and M.-W. Yoo, Current-driven skyrmion dynamics in disordered films, Appl. Phys. Lett. 110, 132404 (2017).
[60]: J. Müller and A. Rosch, Capturing of a magnetic skyrmion with a hole, Phys. Rev. B 91, 054410 (2015).
[61]: C. Reichhardt and C.J.O. Reichhardt, Magnus-induced dynamics of driven skyrmions on a quasi-one-dimensional periodic substrate, Phys. Rev. B 94, 094413 (2016).
[62]: C. Navau, N. Del-Valle, and A. Sanchez, Analytical trajectories of skyrmions in confined geometries: Skyrmionic racetracks and nano-oscillators, Phys. Rev. B 94, 184104 (2016).
[63]: D. Stosic, T.B. Ludermir, and M.V. Milosevic, Pinning of magnetic skyrmions in a monolayer Co film on Pt(111): Theoretical characterization and exemplified utilization, Phys. Rev. B 96, 214403 (2017).
[64]: C. Reichhardt and C.J.O. Reichhardt, Noise fluctuations and drive dependence of the skyrmion Hall effect in disordered systems, New J. Phys. 18, 095005 (2016).
[65]: S.A. Díaz, C.J.O. Reichhardt, D.P. Arovas, A. Saxena, and C. Reichhardt, Fluctuations and noise signatures of driven magnetic skyrmions, Phys. Rev. B 96, 085106 (2017).
[66]: C. Reichhardt, D. Ray, and C.J.O. Reichhardt, Quantized transport for a skyrmion moving on a two-dimensional periodic substrate, Phys. Rev. B 91, 104426 (2015).
[67]: W. Koshibae and N. Nagaosa, Theory of current-driven skyrmions in disordered magnets, Sci. Rep. 8, 6328 (2018).
[68]: J. White et al., to be published.
[69]: S. Torquato, Hyperuniformity and its generalizations, Phys. Rev. E 94, 022122 (2016).
[70]: Q. Le Thien, D. McDermott, C. J. O. Reichhardt, and C. Reichhardt, Enhanced pinning for vortices in hyperuniform pinning arrays and emergent hyperuniform vortex configurations with quenched disorder, Phys. Rev. B 96, 094516 (2017).
[71]: J.M. Schwarz and D.S. Fisher, Depinning with dynamic stress overshoots: A hybrid of critical and pseudohysteretic behavior, Phys. Rev. E 67, 021603 (2003).
[72]: C. J. Olson and C. Reichhardt, Transverse depinning in strongly driven vortex lattices with disorder, Phys. Rev. B 61, R3811(R) (2000).
[73]: H. Fangohr, P.A.J. de Groot, and S.J. Cox, Critical transverse forces in weakly pinned driven vortex systems, Phys. Rev. B 63, 064501 (2001).
[74]: C. Reichhardt and C.J.O. Reichhardt, Devil's staircase and disordering transitions in sliding vortices and Wigner crystals on random substrates with transverse driving, Phys. Rev. B 76, 214305 (2007).
[75]: E. Granato, J.A.P. Ramos, C.V. Achim, J. Lehikoinen, S.C. Ying, T. Ala-Nissila, and K.R. Elder, Glassy phases and driven response of the phase-field-crystal model with random pinning, Phys. Rev. E 84, 031102 (2011).
[76]: A.M. Troyanovski, J. Aarts and P.H. Kes, Collective and plastic vortex motion in superconductors at high flux densities, Nature (London) 399, 665 (1999).
[77]: J. Lefebvre, M. Hilke, and Z. Altounian, Transverse depinning in weakly pinned vortices driven by crossed ac and dc currents, Phys. Rev. B 78, 134506 (2008).
[78]: C. Reichhardt and F. Nori, Phase locking, devil's staircases, Farey trees, and Arnold tongues in driven vortex lattices with periodic pinning, Phys. Rev. Lett. 82, 414 (1999).
[79]: P.T. Korda, M.B. Taylor, and D.G. Grier, Kinetically locked-in colloidal transport in an array of optical tweezers, Phys. Rev. Lett. 89, 128301 (2002).
[80]: A.M. Lacasta, J.M. Sancho, A.H. Romero, and K. Lindenberg, Sorting on periodic surfaces, Phys. Rev. Lett. 94, 160601 (2005).
[81]: M. Balvin, E. Sohn, T. Iracki, G. Drazer, and J. Frechette, Directional locking and the role of irreversible interactions in deterministic hydrodynamics separations in microfluidic devices, Phys. Rev. Lett. 103, 078301 (2009).
[82]: C. Reichhardt and C.J.O. Reichhardt, Dynamical ordering and directional locking for particles moving over quasicrystalline substrates, Phys. Rev. Lett. 106, 060603 (2011).
[83]: T. Bohlein and C. Bechinger, Experimental observation of directional locking and dynamical ordering of colloidal monolayers driven across quasiperiodic substrates, Phys. Rev. Lett. 109, 058301 (2012).
[84]: C. Reichhardt, D. Ray, and C.J.O. Reichhardt, Nonequilibrium phases and segregation for skyrmions on periodic pinning arrays, Phys. Rev. B 98, 134418 (2018)
[86]: X. Yu, D. Morikawa, T. Yokouchi, K. Shibata, N. Kanazawa, F. Kagawa, T. Arima and Y. Tokura, Aggregation and collapse dynamics of skyrmions in a non-equilibrium state, Nature Phys. 14, 832 (2018).
[87]: F. Büttner, C. Moutafis, M. Schneider, B. Krüger, C. M. Günther, J. Geilhufe, C. v. Korff Schmising, J. Mohanty, B. Pfau, S. Schaffert, A. Bisig, M. Foerster, T. Schulz, C. A. F. Vaz, J. H. Franken, H. J. M. Swagten, M. Kläui, and S. Eisebitt, Dynamics and inertia of skyrmionic spin structures, Nat. Phys. 11, 225 (2015).
[88]: C. Schütte, J. Iwasaki, A. Rosch, and N. Nagaosa, Inertia, diffusion, and dynamics of a driven skyrmion, Phys. Rev. B 90, 174434 (2014).
[89]: S. K. Kim, K.-J. Lee, and Y. Tserkovnyak, Self-focusing skyrmion racetracks in ferrimagnets, Phys. Rev. B 95, 140404(R) (2017).
[90]: V. P. Kravchuk, D. D. Sheka, U. K. Rößler, Jeroen van den Brink, and Yuri Gaididei, Spin eigenmodes of magnetic skyrmions and the problem of the effective skyrmion mass, Phys. Rev. B 97, 064403 (2018).
[91]: S. Woo, K. M. Song, H.-S. Han, M.-S. Jung, M.-Y. Im, K.-S. Lee, K. S. Song, P. Fischer, J.-I. Hong, J. W. Choi, B.-C. Min, H. C. Koo, and J. Chang, Spin-orbit torque-driven skyrmion dynamics revealed by time-resolved X-ray microscopy, Nat. Commun. 8, 15573 (2017).
[92]: W. Wang, M. Beg, B. Zhang, W. Kuch, and H. Fangohr, Driving magnetic skyrmions with microwave fields, Phys. Rev. B 92, 020403(R) (2015).
[93]: Y. Liu, H. Yan, M. Jia, H. Du, A. Du, and J. Zang, Field-driven oscillation and rotation of a multiskyrmion cluster in a nanodisk, Phys. Rev. B 95, 134442 (2017).
[94]: M. Ikka, A. Takeuchi, and M. Mochizuki, Resonance modes and microwave-driven translational motion of a skyrmion crystal under an inclined magnetic field, Phys. Rev. B 98, 184428 (2018).
[95]: C. Schütte and M. Garst, Magnon-skyrmion scattering in chiral magnets, Phys. Rev. B 90, 094423 (2014).
[96]: C. Reichhardt, C. J. Olson, and F. Nori, Dynamic vortex phases and pinning in superconductors with twin boundaries, Phys. Rev. B 61, 3665 (2000).
[97]: J. Zázvorka, F. Jakobs, D. Heinze, N. Keil, S. Kromin, S. Jaiswal, K. Litzius, G. Jakob, P. Virnau, D. Pinna, K. Everschor-Sitte, A. Donges, U. Nowak, and M. Kläui, Thermal skyrmion diffusion applied in probabilistic computing, arXiv:1805.05924 (unpublished).
[98]: C. Reichhardt and C. J. O. Reichhardt, Thermal creep and the skyrmion Hall angle in driven skyrmion crystals, J. Phys.: Condens. Matter 31, 07LT01 (2019).
[99]: J. Barker and O. A. Tretiakov, Static and dynamical properties of antiferromagnetic skyrmions in the presence of applied current and temperature, Phys. Rev. Lett. 116, 147203 (2016).
[100]: C. A. Akosa, O. A. Tretiakov, G. Tatara, and A. Manchon, Theory of the topological spin Hall effect in antiferromagnetic skyrmions: Impact on current-induced motion, Phys. Rev. Lett. 121, 097204 (2018).
[101]: A. K. Nayak, V. Kumar, T. Ma, P. Werner, E. Pippel, R. Sahoo, F. Damay, U. K. Rößler, C. Felser, and S. S. P. Parkin, Magnetic antiskyrmions above room temperature in tetragonal Heusler materials, Nature (London) 548, 561 (2017).
[102]: X. Zhang, J. Xia, Y. Zhou, X. Liu, H. Zhang, and M. Ezawa, Skyrmion dynamics in a frustrated ferromagnetic film and current-induced helicity locking-unlocking transition, Nat. Comm. 8, 1717 (2017).
[103]: K. Karube, J. S. White, D. Morikawa, C. D. Dewhurst, R. Cubitt, A. Kikkawa, X. Yu, Y. Tokunaga, T. Arima, H. M. Rønnow, Y. Tokura, and Y. Taguchi, Disordered skyrmion phase stabilized by magnetic frustration in a chiral magnet, Sci. Adv. 4, eaar7043 (2018).
[104]: C.J.O. Reichhardt and C. Reichhardt, Disordering, clustering, and laning transitions in particle systems with dispersion in the Magnus term, Phys. Rev. E 99, 012606 (2019).

File translated from T_EX by T_THgold, version 4.00.
Back to Home