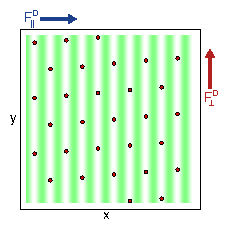
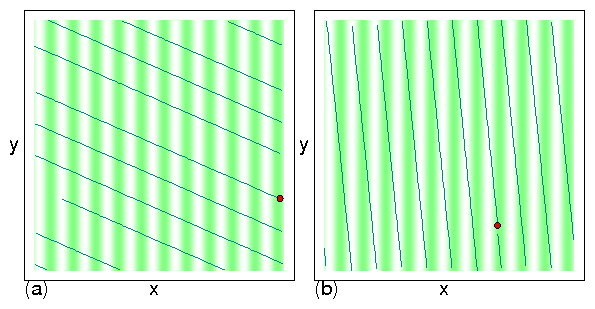
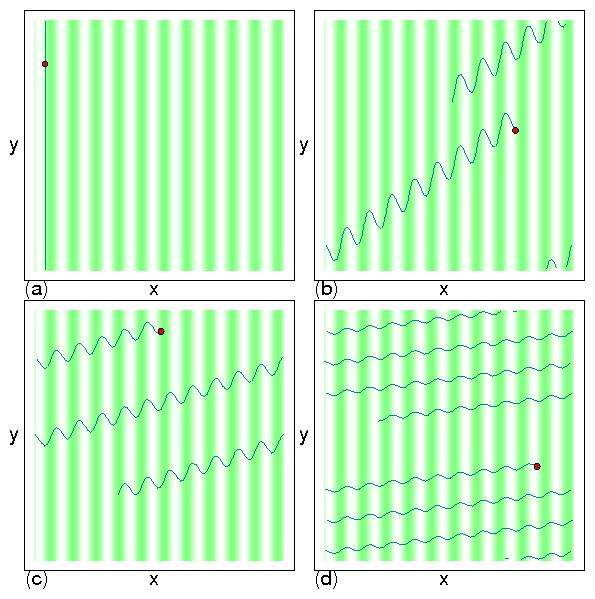
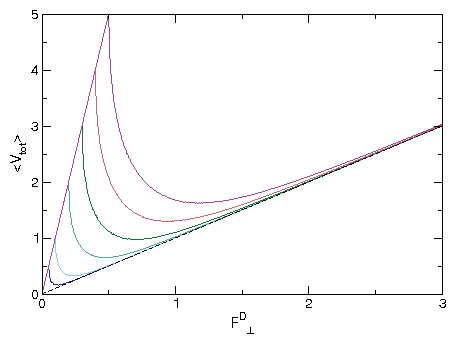
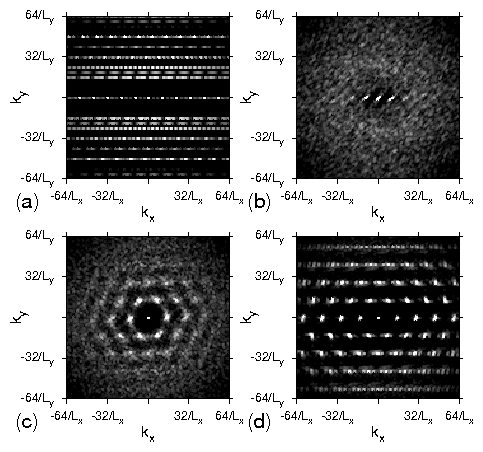
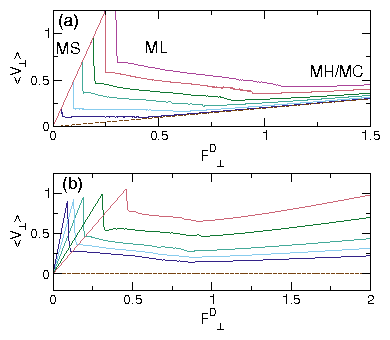
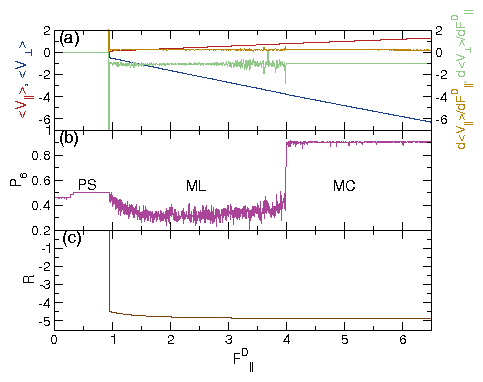
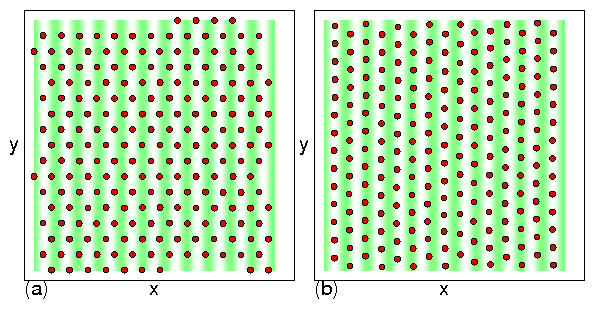
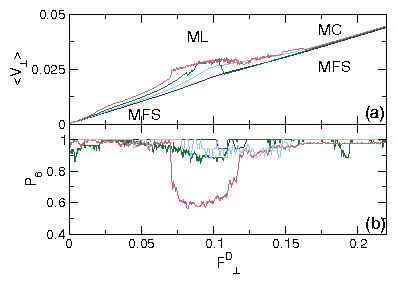
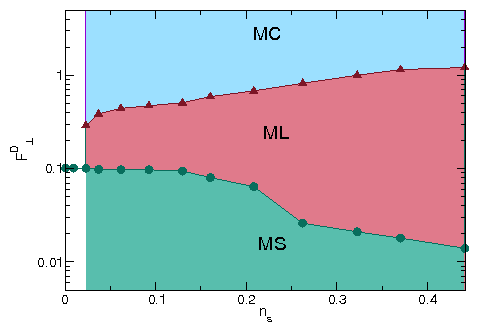
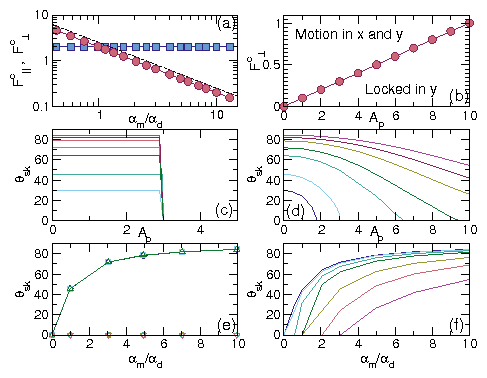
 Figure 7: (a)
The depinning forces Fc|| and Fc⊥ at which motion in the direction
parallel to the substrate periodicity
occurs vs αm/αd for samples with Ap=2.0.
Blue squares: Fc||, for parallel driving,
has no dependence on αm/αd.
Red circles: Fc⊥, for perpendicular driving,
can be fit to
Fc⊥ ∝ (αm/αd)−1 (dashed line).
(b) Fc⊥ vs Ap at
αm/αd = 9.962.
Here Fc⊥ increases linearly with Ap.
(c) The skyrmion Hall angle θsk vs Ap for parallel driving
under constant FD|| = 3.0 at
αm/αd = 9.9624, 7.018, 4.924, 3.042, 2.06, 0.98,
0.577, and 0, from top to bottom.
Here θsk is constant until Ap > 3.0,
after which the system becomes pinned.
(d) θsk vs Ap for perpendicular driving under constant
FD⊥=3.0 at
αm/αd = 9.9624, 7.018, 4.924, 3.042, 2.06, 0.98,
0.577, and 0, from top to bottom.
Here θsk shows a
strong dependence on Ap.
(e)
θsk vs αm/αd
at constant F||D = 3.0
for Ap = 0.0 (circles), 1.0 (squares), 2.0 (diamonds),
3.0 (up triangles), 5.0 (left triangles), and 10.0 (down triangles).
Here, in the moving state for Ap < 3.0, θsk is independent of Ap
and follows the upper curve, while in the pinned state for Ap ≤ 3.0,
θsk=0 (lower curve).
(f)
θsk vs αm/αd
at constant F||D = 3.0
for Ap = 0, 1.0, 2.0, 3.0. 5.0, 7.0, and 10.0,
from top to bottom,
showing that for any fixed value of αm/αd, θsk decreases
with increasing Ap.
Figure 7: (a)
The depinning forces Fc|| and Fc⊥ at which motion in the direction
parallel to the substrate periodicity
occurs vs αm/αd for samples with Ap=2.0.
Blue squares: Fc||, for parallel driving,
has no dependence on αm/αd.
Red circles: Fc⊥, for perpendicular driving,
can be fit to
Fc⊥ ∝ (αm/αd)−1 (dashed line).
(b) Fc⊥ vs Ap at
αm/αd = 9.962.
Here Fc⊥ increases linearly with Ap.
(c) The skyrmion Hall angle θsk vs Ap for parallel driving
under constant FD|| = 3.0 at
αm/αd = 9.9624, 7.018, 4.924, 3.042, 2.06, 0.98,
0.577, and 0, from top to bottom.
Here θsk is constant until Ap > 3.0,
after which the system becomes pinned.
(d) θsk vs Ap for perpendicular driving under constant
FD⊥=3.0 at
αm/αd = 9.9624, 7.018, 4.924, 3.042, 2.06, 0.98,
0.577, and 0, from top to bottom.
Here θsk shows a
strong dependence on Ap.
(e)
θsk vs αm/αd
at constant F||D = 3.0
for Ap = 0.0 (circles), 1.0 (squares), 2.0 (diamonds),
3.0 (up triangles), 5.0 (left triangles), and 10.0 (down triangles).
Here, in the moving state for Ap < 3.0, θsk is independent of Ap
and follows the upper curve, while in the pinned state for Ap ≤ 3.0,
θsk=0 (lower curve).
(f)
θsk vs αm/αd
at constant F||D = 3.0
for Ap = 0, 1.0, 2.0, 3.0. 5.0, 7.0, and 10.0,
from top to bottom,
showing that for any fixed value of αm/αd, θsk decreases
with increasing Ap.
|