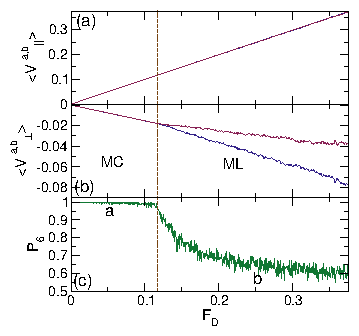
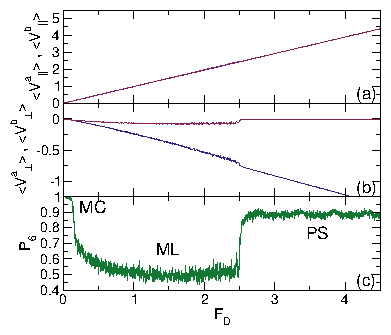
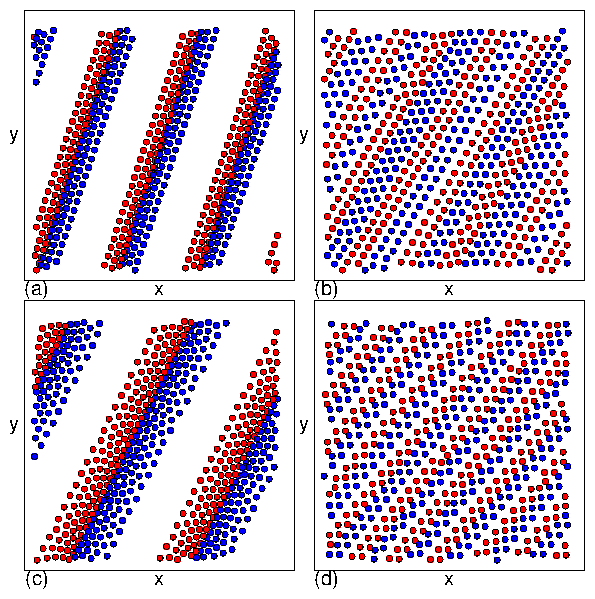
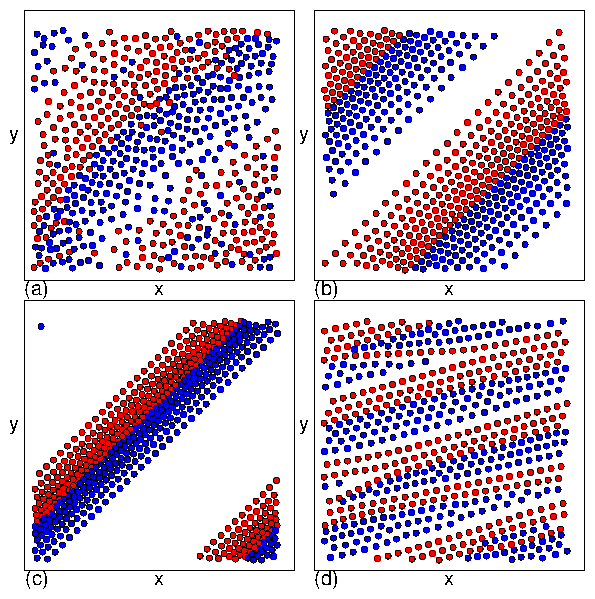
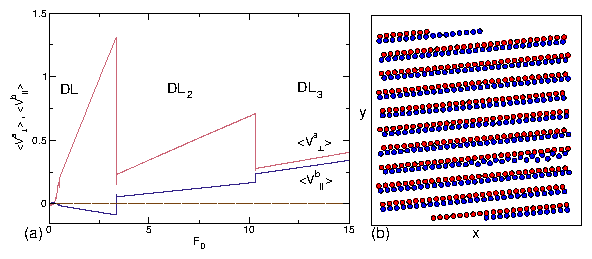
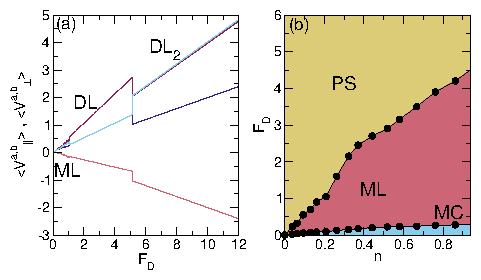
 Figure 23: (a)
〈Va||〉 (dark red),
〈Vb||〉 (dark blue),
〈Va⊥〉 (pink)
and 〈Vb⊥〉 (light blue)
versus FD
for a system with
αbd = 1.0, αad = 2.0,
αam = 0.1, and αbm = −1.0, where
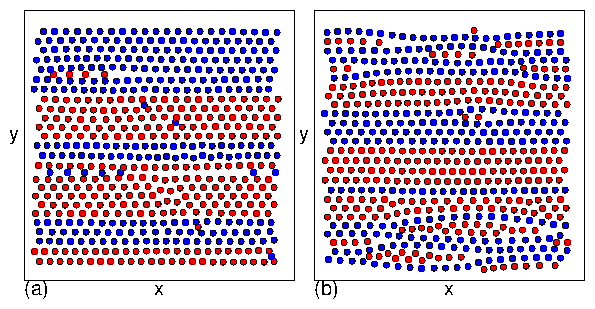
a series of pronounced jumps indicate
transitions into different
DL and DL2 phases.
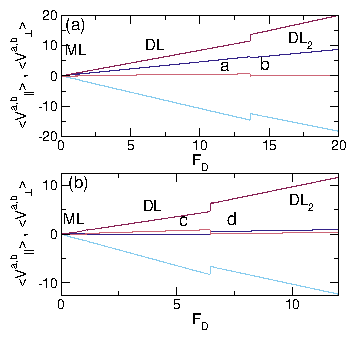
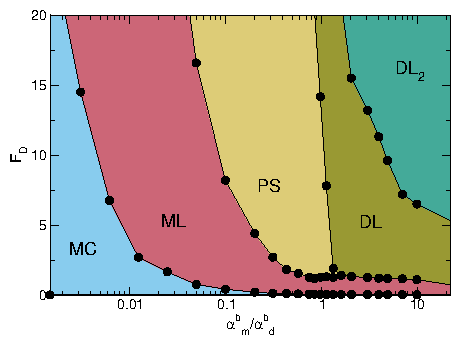
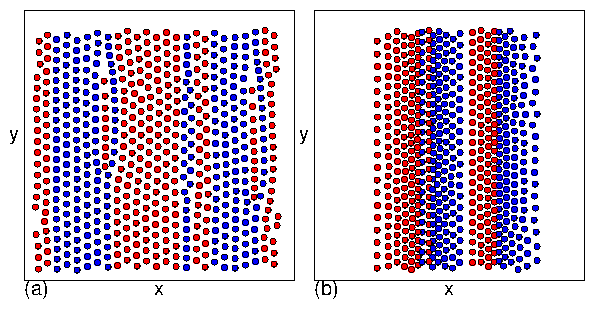
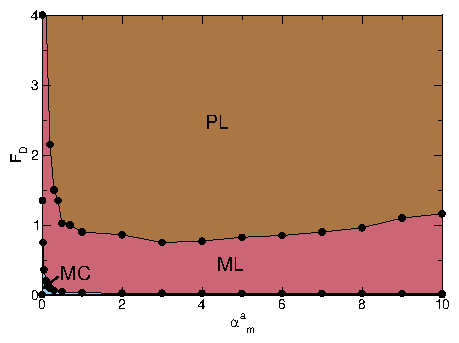
(b) Dynamic phase diagram as a function of
FD vs system density n for
samples with
αad = αbd = 1.0,
αam = 0, and αbm = 0.3,
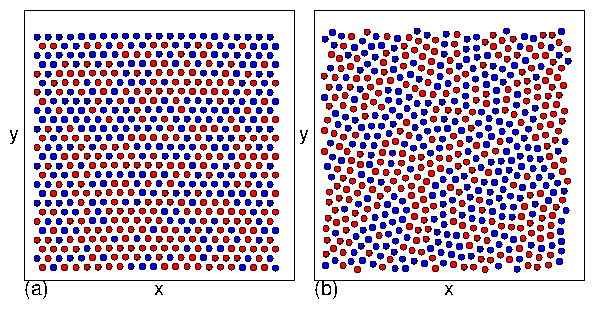
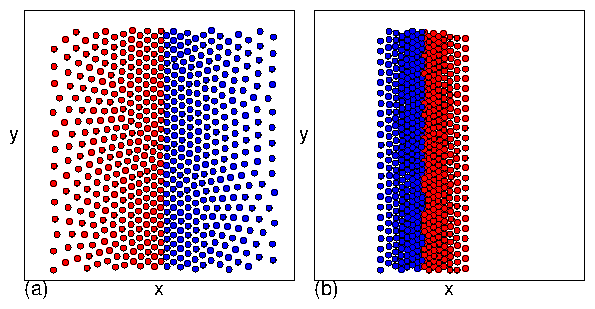
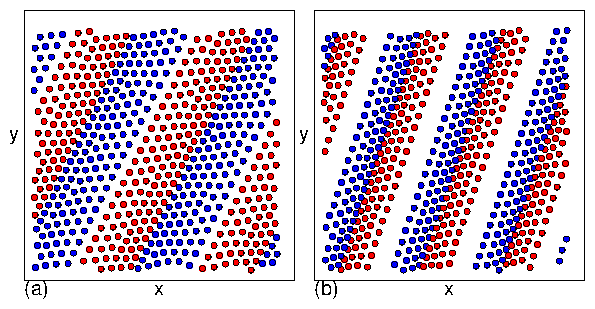
showing that the transitions between the moving crystal (MC),
moving liquid (ML), and perpendicular stripe (PS) phases shift to
higher values of FD with increasing density.
Figure 23: (a)
〈Va||〉 (dark red),
〈Vb||〉 (dark blue),
〈Va⊥〉 (pink)
and 〈Vb⊥〉 (light blue)
versus FD
for a system with
αbd = 1.0, αad = 2.0,
αam = 0.1, and αbm = −1.0, where
a series of pronounced jumps indicate
transitions into different
DL and DL2 phases.
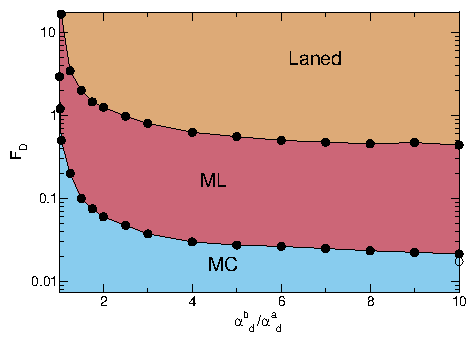
(b) Dynamic phase diagram as a function of
FD vs system density n for
samples with
αad = αbd = 1.0,
αam = 0, and αbm = 0.3,
showing that the transitions between the moving crystal (MC),
moving liquid (ML), and perpendicular stripe (PS) phases shift to
higher values of FD with increasing density.
|