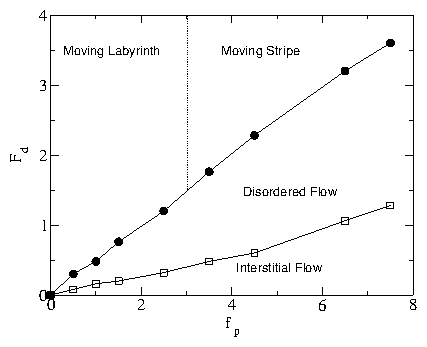
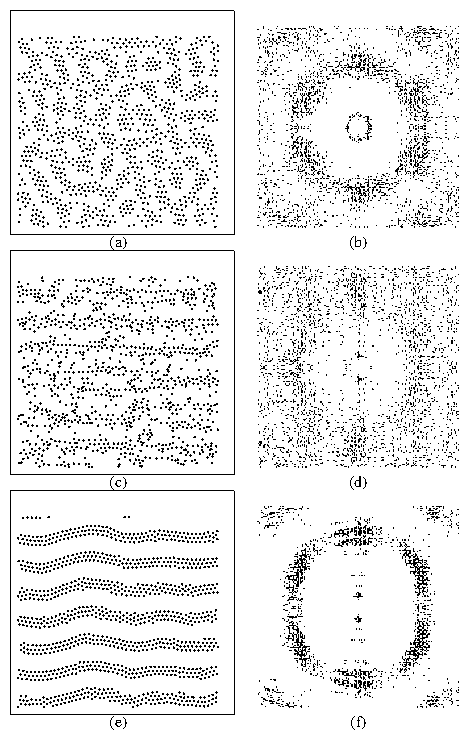
 Figure 1:
(a,c,e) Real space images of the particle locations;
(b,d,f) corresponding structure factor S(k) for:
(a,b) The moving labyrinth phase for fp = 0.5.
(c,d) The interstitial flow regime for fp = 6.5.
(e,f) The moving stripe regime for fp = 6.5.
In each case the number of particles Ni = 1280 and pinning
sites Np = 400.
Figure 1:
(a,c,e) Real space images of the particle locations;
(b,d,f) corresponding structure factor S(k) for:
(a,b) The moving labyrinth phase for fp = 0.5.
(c,d) The interstitial flow regime for fp = 6.5.
(e,f) The moving stripe regime for fp = 6.5.
In each case the number of particles Ni = 1280 and pinning
sites Np = 400.
|