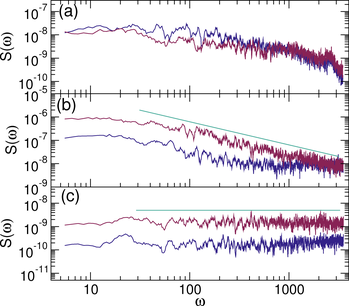
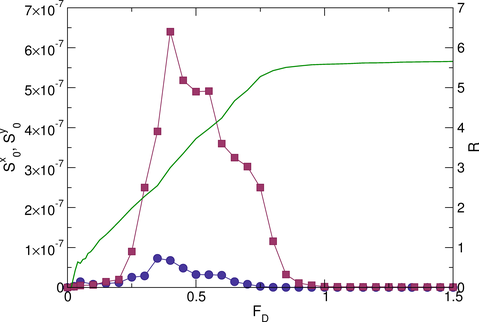
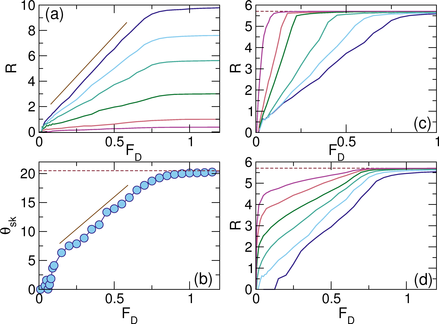
 Figure 3:
(a) R vs FD for samples with Fp = 1.0
and np = 0.1 at
αm/αd = 9.962,
7.7367, 5.708, 3.042, 1.00, and 0.3737, from left to right. The line indicates
a linear fit.
(b) θsk = tan−1(R) for αm/αd = 0.3737 from panel (a).
The solid line is a linear fit
and the dashed line indicates the clean limit value of θsk = 20.5°.
(c) R vs FD for αm/αd = 5.708
at Fp = 0.06125, 0.125, 0.25, 0.5, 0.75, and 1.0, from left
to right.
(d) R vs FD for Fp = 1.0 at
αm/αd = 5.708 for
np = 0.00617, 0.01234, 0.02469, 0.04938, 0.1, and 0.2, from left to right.
The clean limit value of R is indicated by the dashed line.
Figure 3:
(a) R vs FD for samples with Fp = 1.0
and np = 0.1 at
αm/αd = 9.962,
7.7367, 5.708, 3.042, 1.00, and 0.3737, from left to right. The line indicates
a linear fit.
(b) θsk = tan−1(R) for αm/αd = 0.3737 from panel (a).
The solid line is a linear fit
and the dashed line indicates the clean limit value of θsk = 20.5°.
(c) R vs FD for αm/αd = 5.708
at Fp = 0.06125, 0.125, 0.25, 0.5, 0.75, and 1.0, from left
to right.
(d) R vs FD for Fp = 1.0 at
αm/αd = 5.708 for
np = 0.00617, 0.01234, 0.02469, 0.04938, 0.1, and 0.2, from left to right.
The clean limit value of R is indicated by the dashed line.
|