 Figure 1:
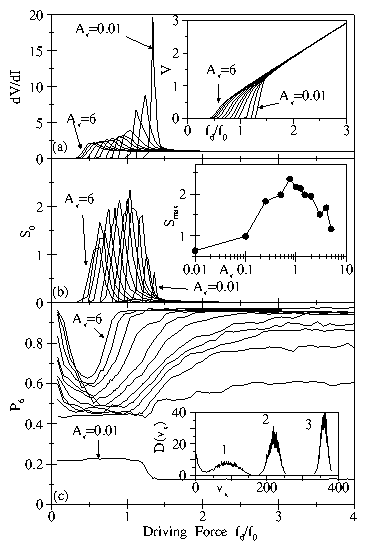
(a): dV/dI curves for vortex-vortex interactions
(right to left) Av = 0.01, 0.1, 0.25, 0.5, 0.75, 1, 1.5, 2, 3, 4, 5, 6.
The peak in dV/dI increases in magnitude with decreasing Av.
Inset to (a): Voltage-current V(I) curves for the Av values listed
above.
The depinning transition shifts to higher driving
currents fd and becomes more abrupt as Av decreases.
(b): Voltage noise power S0 versus fd for the Av
values listed above. In each case the noise power peaks
during the plastic
flow regime. Inset to (b): Maximum noise power Smax as a function
of Av. The peak value of Smax corresponds to
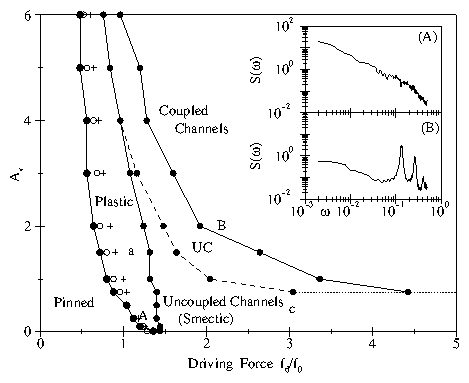
Av ≈ 0.75, the same Av at which the system crosses
between smectic and coupled channel behavior at high drives.
(c): Fraction of six-fold coordinated vortices P6 as a function
of fd for values of Av listed above.
At zero drive and strong VL coupling,
P6 ∼ 1 since the VL is field-cooled.
The lowest value of P6 at each Av corresponds exactly to the
peak in dV/dI. The VL eventually reorders to P6 ∼ 1 only
when Av ≥ 1. For Av ≤ 0.75,
P6 saturates at a value below 1.
Inset to (c): Velocity distribution functions D(vx)
for (1) plastic, (2) smectic,
and (3) coupled channel phases.
Figure 1:
(a): dV/dI curves for vortex-vortex interactions
(right to left) Av = 0.01, 0.1, 0.25, 0.5, 0.75, 1, 1.5, 2, 3, 4, 5, 6.
The peak in dV/dI increases in magnitude with decreasing Av.
Inset to (a): Voltage-current V(I) curves for the Av values listed
above.
The depinning transition shifts to higher driving
currents fd and becomes more abrupt as Av decreases.
(b): Voltage noise power S0 versus fd for the Av
values listed above. In each case the noise power peaks
during the plastic
flow regime. Inset to (b): Maximum noise power Smax as a function
of Av. The peak value of Smax corresponds to
Av ≈ 0.75, the same Av at which the system crosses
between smectic and coupled channel behavior at high drives.
(c): Fraction of six-fold coordinated vortices P6 as a function
of fd for values of Av listed above.
At zero drive and strong VL coupling,
P6 ∼ 1 since the VL is field-cooled.
The lowest value of P6 at each Av corresponds exactly to the
peak in dV/dI. The VL eventually reorders to P6 ∼ 1 only
when Av ≥ 1. For Av ≤ 0.75,
P6 saturates at a value below 1.
Inset to (c): Velocity distribution functions D(vx)
for (1) plastic, (2) smectic,
and (3) coupled channel phases.
|