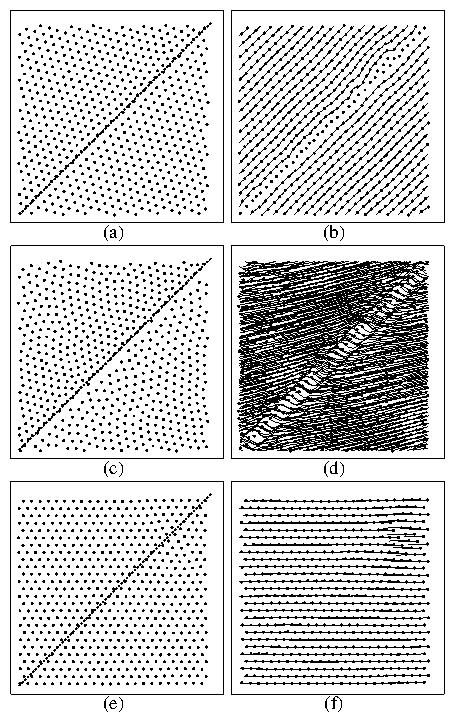
 Figure 1:
The vortex positions (left column) and flow patterns (right column)
for three different applied drives.
Panels (a,b), with fd/f0 = 0.05, show guided plastic motion.
Panels (c,d), with fd/f0 = 0.35 show a slightly more disordered
motion, exhibiting some plasticity, tearing, and healing.
Specifically, the vortex lattice is slightly torn apart by the
twin boundary, but it heals right after crossing it.
Panels (e,f), with fd/f0 = 1.25, show elastic flow.
Figure 1:
The vortex positions (left column) and flow patterns (right column)
for three different applied drives.
Panels (a,b), with fd/f0 = 0.05, show guided plastic motion.
Panels (c,d), with fd/f0 = 0.35 show a slightly more disordered
motion, exhibiting some plasticity, tearing, and healing.
Specifically, the vortex lattice is slightly torn apart by the
twin boundary, but it heals right after crossing it.
Panels (e,f), with fd/f0 = 1.25, show elastic flow.
|
