Physical Review Letters 114, 217202 (2015)

Collective Transport Properties of Driven Skyrmions with Random Disorder

C. Reichhardt, D. Ray, and C. J. Olson Reichhardt

Theoretical Division and Center for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA

(Received 18 September 2014; revised manuscript received 5 February 2015; published 27 May 2015)

We use particle-based simulations to examine the static and driven collective phases of skyrmions interacting with random quenched disorder. We show that non-dissipative effects due to the Magnus term reduce the depinning threshold and strongly affect the skyrmion motion and the nature of the dynamic phases. The quenched disorder causes the Hall angle to become drive-dependent in the moving skyrmion phase, while different flow regimes produce distinct signatures in the transport curves. For weak disorder, the skyrmions form a pinned crystal and depin elastically, while for strong disorder the system forms a pinned amorphous state that depins plastically. At high drives the skyrmions can dynamically reorder into a moving crystal, with the onset of reordering determined by the strength of the Magnus term.
Simulation and System
Results and Discussion
Summary
References
A wide variety of systems can be effectively modeled as collectively interacting particles moving over quenched disorder, with a transition from a pinned state to a sliding state under an applied drive. Examples include driven incommensurate charge density waves [1,2], Wigner crystals [3,4], colloids on various types of substrates [5,6,7], and vortices in type-II superconductors [8,9,10,11,12]. In many of these systems the particle-particle interactions are repulsive, so that in the absence of disorder a hexagonal crystal of particles forms. When quenched disorder is present, the particles may retain mostly hexagonal order if the disorder is weak, while stronger disorder can cause a proliferation of topological defects creating an amorphous or glassy state [8,9,13]. When an external driving force FD is applied to pinned particles, the particles begin to move above a critical drive value Fc known as the depinning threshold. For weak disorder the particles generally depin elastically and retain their original neighbors [1,2,5,7,9], but for strong disorder the depinning becomes plastic with particles continuously changing neighbors over time, forming a fluctuating liquid-like state [4,5,6,9,10,11,12]. When depinning occurs from a disordered pinned state, there can be dynamic structural transitions at drives well above Fc, where the particles dynamically order into a moving anisotropic crystal or moving smectic phase [9,10,11,14,15,16,17,18,19,20] when the strong driving reduces the effectiveness of the pinning in the drive direction [10]. Transitions from pinned to plastic and from plastic to dynamically ordered states have been observed experimentally through features in transport measures [1,6,9,11], neutron scattering [14], changes in noise fluctuations [11], and direct imaging [18].
Recently a new type of system, skyrmions in chiral magnets, has been realized that can be effectively characterized as particle-like objects interacting with random disorder [21,22,23]. Neutron scattering experiments showed evidence for triangular skyrmion lattices in bulk MnSi samples [22], and subsequent Lorentz microscopy experiments [22,23,24] produced direct observations of skyrmion lattices. Imaging measurements indicate that as an externally applied magnetic field is increased, a low-density, partially-disordered skyrmion phase emerges from a helical phase before forming a denser ordered triangular lattice of skyrmions. At high fields, the skyrmion number decreases and the system enters a uniform ferromagnetic state [22,23]. Similar to vortices in type-II superconductors, skyrmions have a particle-like nature and can be externally driven by the application of a current [25]. Experimental transport measurements show [26] that it is possible to obtain skyrmion velocity versus applied driving force curves with a finite depinning threshold. The current-driven motion of skyrmions has also been directly experimentally imaged [27,28].
One aspect of skyrmions that makes them very distinct from other collectively driven systems in random disorder is the pronounced non-dissipative component in the equation of motion arising from the Magnus term [23,29,30,31]. This term causes skyrmions to move perpendicular to the applied driving force, and it has been argued to be responsible for the low depinning threshold observed for skyrmions [23,29,30,31]. The strength of the Magnus term is denoted by αm while that of the damping is denoted by αd. In superconducting vortex systems, αm/αd << 1.0 so the non-dissipative terms are very weak [8], whereas skyrmion systems typically have αm/αd  ∼ 10 to 40 so that the Magnus term dominates. This makes skyrmions a unique system in which to explore non-dissipative collective dynamics. Beyond basic science issues, skyrmions may be useful for a range of applications [32] which will require an understanding of skyrmion dynamics in the presence of disorder.
Here we utilize a recently developed particle-based model for skyrmion dynamics to study collective skyrmion behaviors in the presence of random quenched disorder for varied disorder strengths and varied αm/αd. We show that the Magnus term reduces the depinning threshold and induces orbits with a circular character for skyrmions moving over pinning sites, while collective skyrmion-skyrmion interactions contribute to the reduction of the depinning threshold. We find that the Magnus term introduces a Hall angle for the skyrmion motion relative to the direction of the external drive, and that inclusion of quenched disorder strongly reduces this Hall angle, especially near depinning. At higher drives, the velocity-force curves both parallel and perpendicular to the drive show distinctive features associated with a transition into a dynamically ordered state. We also find disorder-induced transitions from a skyrmion glass to a skyrmion crystal phase as a function of disorder strength or skyrmion density.
Fig1.png
Figure 1: Real-space image of skyrmions (dark red dots) driven through randomly arranged pinning sites (light blue dots) for a plastic flow phase at Fp = 0.03 and FD = 0.0125. The trajectory of a single skyrmion is highlighted, showing spiraling motions inside the pinning sites.
Simulation and System- We simulate skyrmions interacting with random disorder using a recently developed particle model [31] valid for low to moderate drives in the sparse limit where the skyrmion separation and size are comparable. The dynamics of a single skyrmion i is governed by the following equation:
αd vi + αm
^
z
 
 ×vi = Fssi + Fspi + FD .
(1)
Here vi = d ri/dt is the skyrmion velocity. The damping term αd aligns the skyrmion velocity with the net force acting on the skyrmion, while the Magnus term αm rotates the velocity into the perpendicular direction. We impose the constraint αd2 + αm2 = 1 to maintain a constant magnitude of the skyrmion velocity as αm/αd varies. For systems such as MnSi [31], αm/αd ≈ 10; unless otherwise noted, we take αm/αd=9.962, corresponding to Magnus-dominated particle dynamics. The skyrmion-skyrmion interaction force is Fssi = ∑Nsj=1 ∧rij K1(Rij) where Rij=|ri − rj|, ∧rij=(ri − rj)/Rij, and K1 is the modified Bessel function which falls off exponentially for large Rij. The pinning force Fspi arises from randomly placed, non-overlapping harmonic traps of size Rp=0.3 [31,33] with a maximum pinning force of Fp. The driving term FD represents a Lorentz force from an externally applied current interacting with the emergent magnetic flux carried by the skyrmions [26].
Our system is of size L ×L with L=36, has periodic boundary conditions in the x and y directions, and contains Ns skyrmions and Np pinning sites. The pin density ρp=Np/L2 is fixed at 0.3, and the skyrmion density ρs=Ns/L2 is 0.1 unless otherwise noted. We apply a slowly increasing driving force FD and measure the average skyrmion velocity in the direction parallel (perpendicular) to the applied drive, 〈Vdrive 〉 (〈V⊥ 〉). The Hall angle is θ = tan−1R, where R = 〈V⊥〉/〈Vdrive〉. For a single skyrmion driven in the absence of disorder, R = αm/αd, so that θ = 84.25° in the clean limit; in contrast, a superconducting vortex with αm/αd ≈ 0.0 would have θ ≈ 0° and move in the direction of drive.
For comparison with experiment, consider an MnSi thin film [31] with lattice constant a ≈ 0.5 nm, exchange energy J ≈ 3 meV/a, and Dzyaloshinskii-Moriya energy D ≈ 0.3 meV/a2. The skyrmion size and lattice constant are ξ ∼ 2πJ / D ≈ 30 nm, so ρs=0.1 implies a length unit of l0 ≈ ξ√{ρs}  ∼ 10 nm, smaller than but comparable to ξ. The force unit is F0  ∼ 10−5 N/m, the skyrmion-skyrmion repulsive force per length at a separation of l0 [31]. The value Fp=0.03 corresponds to a depinning force for an isolated skyrmion of 0.03F0 = 3×10−7 N/m. From the expression for the Lorentz force on a skyrmion[31], FL=(h/e)J, the corresponding depinning current is  ∼ 108 A/m2. Similar mappings of the simulation parameters can be performed for other materials.
Results and Discussion- In Fig. 1 we show a snapshot of skyrmions moving through random disorder in a small portion of a system with Fp = 0.03 and FD = 0.0125. Since this drive is well above the depinning threshold Fc ≈ 0.00625, all the skyrmions are in motion. We highlight the trajectory of a single skyrmion, which, due to the Magnus term, undergoes a circular motion within each pinning site it encounters. The force from each pinning site points toward the pin center, but under Magnus-dominated dynamics this force is largely perpendicular to the skyrmion velocity, causing the skyrmion to circle around the inner edge of the pin. In the overdamped limit αm/αd << 1, a particle entering a pinning site would quickly travel to the bottom of the potential well and be strongly pinned. We note that the escape of a skyrmion from a pin is strongly affected by motion excited via interactions with the surrounding skyrmions.
Fig2.png
Figure 2: (a) Average skyrmion velocity in the drive direction, 〈Vdrive 〉 (open squares), and perpendicular to the drive, 〈V⊥ 〉 (filled circles), vs FD for a system with Fp = 0.03. Inset: Hall angle θ vs FD; dotted line is the result for the clean system. (b) Corresponding 〈Vdrive〉 (open squares) and the fraction of sixfold coordinated particles P6 (filled triangles) vs FD; the dashed line shows 〈Vdrive〉 for the clean system. A dynamical ordering transition into a moving crystal state occurs at FD ≈ 0.03.
We first examine how the Hall angle is affected by random disorder. In Fig. 2(a) we plot 〈Vdrive 〉 and 〈V⊥ 〉 versus FD for a system with Fp = 0.03. For FD < 0.00625, the skyrmions are disordered and pinned. Just above depinning, 〈Vdrive 〉 ≈ 〈V⊥ 〉, so that R ≈ 1.0 is much less than the clean-limit value. In general we find that adding quenched disorder decreases 〈V⊥ 〉 and increases 〈Vdrive 〉 compared to the clean limit, indicating that the average skyrmion flow is rotated toward the drive direction. This is illustrated in the inset of Fig. 2(a), which shows that θ falls well below the clean-limit value at low drives and approaches it at higher drives. This behavior originates from a ratcheting effect experienced by the skyrmions as they encounter pins. An applied drive displaces the equilibrium pinned position of a skyrmion from the pin center in the direction of the drive, and a skyrmion driven over a pin is pulled toward this equilibrium point. Consequently, the trajectory of a skyrmion emerging from a pin is offset in the drive direction relative to the incoming trajectory. When FD <~Fp, the skyrmion-pin interaction occurs for an extended time, producing a large offset, while for higher drives, the skyrmion passes quickly through the pin, diminishing the offset. Very recently, a similar dependence of the Hall angle on the drive was observed in the single-skyrmion limit [34].
As shown in Fig. 1, at FD=0.0125 the skyrmions form a disordered state; however, at higher FD they can dynamically order into a moving crystal. In Fig. 2(b) we plot the fraction of six-fold coordinated particles P6 as a function of FD along with 〈Vdrive 〉 for the same system as in Fig. 2(a). Readjustments of skyrmion positions in the pinned state cause P6 to reach its smallest value at depinning where the particles are most disordered [19], but it rapidly approaches 1 around FD ≈ 0.03 indicating dynamical reordering. Simultaneously, 〈Vdrive 〉 acquires a linear dependence on FD and approaches the clean-limit value.
Fig3.png
Figure 3: Dynamical phase diagram for FD vs Fp highlighting the different skyrmion phases. PC: pinned crystal; PG: pinned amorphous glass; ML: moving liquid; MC: moving crystal. Circles: elastic depinning from PC to MC; squares: plastic depinning from PG to ML; triangles: dynamical ordering transition from ML to MC. Upper inset: structure factor S(k) of skyrmion positions in the MC state. Lower inset: S(k) in the ML state.
In Fig. 3 we plot a dynamical phase diagram highlighting the static and dynamic phases for skyrmions as FD and Fp are varied. For Fp < 0.015 the skyrmions form a pinned triangular crystal (PC) which depins elastically to a moving crystal state (MC) as FD increases. For Fp > 0.015 at low drives, we instead find an amorphous pinned skyrmion glass (PG) which depins plastically into a fluctuating moving skyrmion liquid (ML). The lower inset of Fig. 3 shows the structure factor S(k)=Ns−1|∑i=1Nse−ik·ri|2 of the ML phase, which has a liquid-like ring. As FD increases further, the moving liquid dynamically reorders into a moving skyrmion crystal with sixfold ordering, as shown in the upper inset of Fig. 3. At Fp  ∼ 0.015 the energy scales of the skyrmion-pin and skyrmion-skyrmion interactions are equal. This phase diagram has similarities to that found for a driven vortex system [19]; however, the skyrmions reorder into a moving crystal rather than a moving smectic [35]. The vortex moving smectic forms when the pinning remains effective in the direction transverse to the drive but is weakened in the drive direction, subjecting the vortices to an anisotropic effective temperature. For moving skyrmions, additional fluctuations induced by the Magnus force reduce the transverse pinning, giving a more isotropic effective temperature and allowing the skyrmions to form a more isotropic moving structure. Neutron scattering experiments could be used to observe the reordering transition from a skyrmion glass to a moving skyrmion crystal state as a function of external drive. The reordering transition is robust against changes to the pin radius [35].
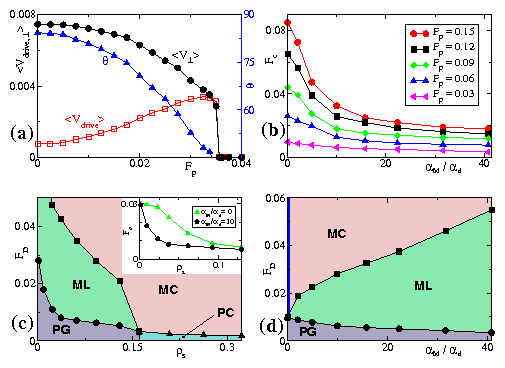
Fig4.png
Figure 4: (a) 〈Vdrive〉, 〈V⊥〉, and θ vs Fp at FD = 0.0075. (b) Critical depinning force Fc vs αm/αd for Fp = 0.15, 0.12, 0.09, 0.06, and 0.03 (top to bottom). (c) Phase diagram for FD vs ρs at Fp = 0.03, highlighting the transitions from PG to ML (circles), ML to MC (squares), and PC to MC (triangles). Inset: Depinning threshold (PG-ML transition line) for Magnus-dominated (circles) and damping-dominated (triangles) systems. (d) Phase diagram of FD vs αm/αd for Fp = 0.03, showing transitions from PG to ML (circles) and ML to MC (squares). Overdamped particles with αm/αd=0 form a moving smectic state (heavy line).
To better understand how the pinning affects skyrmion motion, in Fig. 4(a) we plot 〈Vdrive〉 and 〈V⊥〉 for fixed FD = 0.0075 and varied pinning strength. As Fp increases and the skyrmions transition from MC to ML to PG (shown in Fig. 3), the trajectory offset effect caused by the pinning becomes more prominent with 〈Vdrive 〉 increasing and 〈V⊥ 〉 decreasing from their clean-limit values, and the Hall angle falling to a minimum of 43° at Fp = 0.035, near the pinning transition. In Fig. 4(b) we plot Fc versus αm/αd for varied Fp. As the dynamics become increasingly Magnus-dominated, Fc decreases monotonically, confirming that inclusion of Magnus forces lowers the depinning threshold. This effect is more prominent for higher values of Fp.
To show how collective skyrmion-skyrmion interactions influence the pinning, we fix Fp and vary the skyrmion density ρs to produce the phase diagram shown in Fig. 4(c). At low ρs, a disordered pinned state forms that depins plastically into a moving liquid and then orders into a moving crystal at higher drives. At higher ρs, a pinned crystal state elastically depins directly into a moving crystal state. The depinning threshold is very close to Fp at low ρs near the single skyrmion limit, but drops rapidly as ρs increases, indicating that collective skyrmion-skyrmion interactions play a crucial role in depressing the depinning threshold in a Magnus-dominated system. The inset of Fig. 4(c) shows the plastic depinning threshold for Magnus-dominated and damping-dominated particle dynamics. At low ρs, Fc is nearly the same for the two systems; however, as ρs increases and the skyrmion-skyrmion interactions become important, Fc decreases much more rapidly in the Magnus-dominated system. In Fig. 4(d) we show how the dynamical phase diagram changes as the dynamics become increasingly Magnus-dominated by plotting the phases as a function of FD and αm/αd. When αm/αd = 0, the behavior is the same as that of a vortex system and the system reorders into a moving smectic rather than a moving crystal. As αm/αd increases, the depinning threshold drops while the drive at which dynamical reordering occurs increases due to the enhanced swirling motion of the skyrmions in the liquid state, which produces an effective temperature that is more isotropic and larger in magnitude than the overdamped case.
Summary- We have investigated the depinning dynamics of skyrmions interacting with random disorder, utilizing a particle-based skyrmion model. We find that the Magnus-dominated dynamics of skyrmions decreases the depinning threshold due to the swirling orbits followed by skyrmions interacting with pinning sites. Skyrmion-skyrmion scattering can excite such orbits and also plays an important role in reducing the depinning threshold. For increasing disorder strength we find transitions from a pinned skyrmion crystal to an amorphous skyrmion glass. We also show that the Hall angle deviates from its clean-limit value for strong pinning or weak driving. At high drives, unlike superconducting vortices which dynamically reorder into a smectic state, the skyrmions undergo a dynamical phase transition from a fluctuating driven liquid to a moving crystal since the Magnus term tends to make the fluctuations, and the resulting effective temperature, experienced by the skyrmions more isotropic than in a driven damping-dominated system. Features in the transport response such as velocity-force curves or structure factor measurements can be used to identify the different dynamical phases.
We thank S.-Z. Lin for useful discussions. We gratefully acknowledge the support of the U.S. Department of Energy through the LANL/LDRD program for this work. This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396 and through the LANL/LDRD program.

References

[1]
G. Grüner, Rev. Mod. Phys. 60, 1129 (1988).
[2]
L. Balents and M.P.A. Fisher, Phys. Rev. Lett. 75, 4270 (1995).
[3]
F.I.B. Williams et al., Phys. Rev. Lett. 66, 3285 (1991).
[4]
M.-C. Cha and H.A. Fertig, Phys. Rev. B 50, 14368 (1994).
[5]
C. Reichhardt and C. J. Olson, Phys. Rev. Lett. 89, 078301 (2002).
[6]
A. Pertsinidis and X.S. Ling, Phys. Rev. Lett. 100, 028303 (2008).
[7]
T. Bohlein, J. Mikhael, and C. Bechinger, Nature Mater. 11, 126 (2012).
[8]
G. Blatter, M.V. Feigelman, V.B. Geshkenbein, A.I. Larkin, and V.M. Vinokur, Rev. Mod. Phys. 66, 1125 (1994).
[9]
S. Bhattacharya and M.J. Higgins, Phys. Rev. Lett. 70, 2617 (1993).
[10]
A.E. Koshelev and V.M. Vinokur, Phys. Rev. Lett. 73, 3580 (1994).
[11]
A.C. Marley, M.J. Higgins, and S. Bhattacharya, Phys. Rev. Lett. 74, 3029 (1995).
[12]
Y. Fily, E. Olive, N. Di Scala, and J.C. Soret, Phys. Rev. B 82, 134519 (2010).
[13]
M.-C. Cha and H.A. Fertig, Phys. Rev. Lett. 74, 4867 (1995).
[14]
U. Yaron et al., Nature (London) 376, 753 (1995).
[15]
K. Moon, R.T. Scalettar, and G.T. Zimányi, Phys. Rev. Lett. 77, 2778 (1996).
[16]
T. Giamarchi and P. Le Doussal, Phys. Rev. Lett. 76, 3408 (1996); P. Le Doussal and T. Giamarchi, Phys. Rev. B 57, 11356 (1998).
[17]
L. Balents, M.C. Marchetti, and L. Radzihovsky, Phys. Rev. B 57, 7705 (1998).
[18]
F. Pardo, F. de la Cruz, P.L. Gammel, E. Bucher, and D.J. Bishop, Nature (London) 396, 348 (1998).
[19]
C.J. Olson, C. Reichhardt, and F. Nori, Phys. Rev. Lett. 81, 3757 (1998).
[20]
H. Fangohr, S.J. Cox, and P.A.J. de Groot, Phys. Rev. B 64, 064505 (2001).
[21]
S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii, and P. Böni, Science 323, 915 (2009).
[22]
X.Z. Yu, Y. Onose, N. Kanazawa, J.H. Park, J.H. Han, Y. Matsui, N. Nagaosa, and Y. Tokura, Nature (London) 465, 901 (2010).
[23]
N. Nagaosa and Y. Tokura, Nature Nanotechnol. 8, 899 (2013).
[24]
X.Z. Yu, N. Kanazawa, Y. Onose, K. Kimoto, W.Z. Zhang, S. Ishiwata, Y. Matsui, and Y. Tokura, Nature Mater. 10, 106 (2011).
[25]
F. Jonietz, S. Mühlbauer, C. Pfleiderer, A. Neubauer, W. Münzer, A. Bauer, T. Adams, R. Georgii, P. Böni, R.A. Duine, K. Everschor, M. Garst, and A. Rosch, Science 330, 1648 (2010).
[26]
T. Schulz, R. Ritz, A. Bauer, M. Halder, M. Wagner, C. Franz, C. Pfleiderer, K. Everschor, M. Garst, and A. Rosch, Nature Phys. 8, 301 (2012).
[27]
X.Z. Yu, N. Kanazawa, W.Z. Zhang, T. Nagai, T. Hara, K. Kimoto, Y. Matsui, Y. Onose, and Y. Tokura, Nature Commun. 3, 988 (2012).
[28]
X.Z. Yu, Y. Tokunaga, Y. Kaneko, W.Z. Zhang, K. Kimoto, Y. Matsui, Y. Taguchi, and Y. Tokura, Nature Commun. 5, 3198 (2014).
[29]
J. Iwasaki, M. Mochizuki, and N. Nagaosa, Nature Commun. 4, 1463 (2013).
[30]
J. Iwasaki, M. Mochizuki, and N. Nagaosa, Nature Nanotechnol. 8, 742 (2013).
[31]
S.-Z. Lin, C. Reichhardt, C.D. Batista, and A. Saxena, Phys. Rev. B 87, 214419 (2013).
[32]
A. Fert, V. Cros, and J. Sampaio, Nature Nanotechnol. 8, 152 (2013).
[33]
Ye-Hua Liu and You-Quan Li, J. Phys.: Condens. Matter 25, 076005 (2013).
[34]
J. Müller and A. Rosch, Phys. Rev. B 91, 054410 (2015).
[35]
See Supplemental Material at http://link.aps.org/supplemental/10.1103/PhysRevLett.114.217202 for movies and Rp vs Fd phase diagram.


File translated from TEX by TTHgold, version 4.00.
 Back to Home