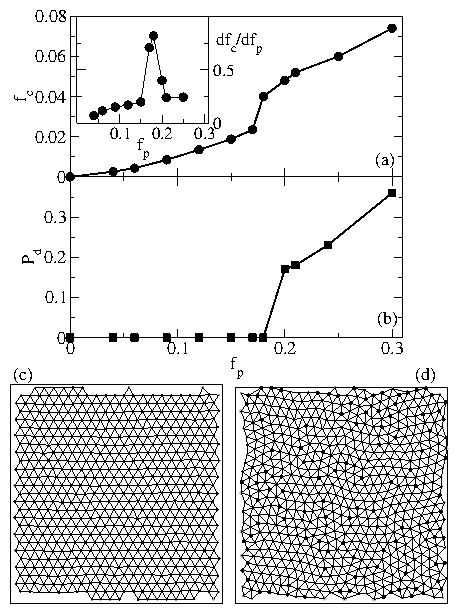
 Figure 4:
Average transient velocity per colloid V/Nc vs time in the disordered
region for fp = 0.25 at a sudden applied drive of
(from top to bottom)
fd/fc = 1.2, 1.0, 0.8, 0.6, and 0.3. A stretched
exponential A exp(−(t/t0)α) + v1 can be fit to all the
curves. Bottom curve: a stretched exponential fit for
the fd/fc=0.3 case, with
V/Nc = 0.0089 exp(−(t/400)1) + 0.
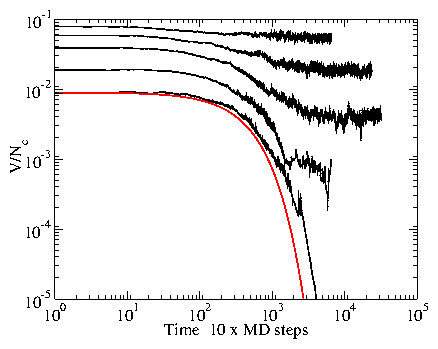
Figure 4:
Average transient velocity per colloid V/Nc vs time in the disordered
region for fp = 0.25 at a sudden applied drive of
(from top to bottom)
fd/fc = 1.2, 1.0, 0.8, 0.6, and 0.3. A stretched
exponential A exp(−(t/t0)α) + v1 can be fit to all the
curves. Bottom curve: a stretched exponential fit for
the fd/fc=0.3 case, with
V/Nc = 0.0089 exp(−(t/400)1) + 0.
|