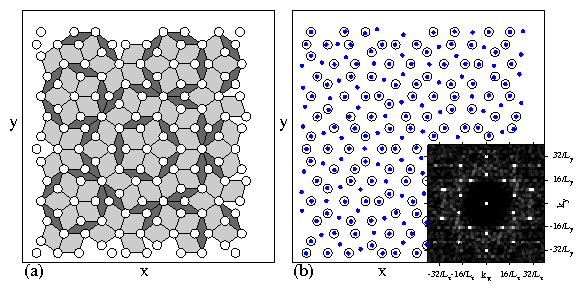
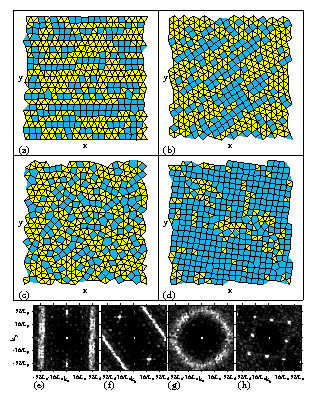
 Figure 3:
Delaunay triangulations of the particle
positions in the sliding state.
Bonds longer than 1.1a0 are omitted, where a0 is the lattice spacing
of a triangular lattice with the same density.
Yellow (light) polygons are triangular and blue (dark) polygons are square
or nontriangular.
For a sample with B/Bϕ=3.225
and FD=2.0 we show
(a) the 0/1 step at θ = 0 exhibiting the oriented triangles and squares
of the dynamically induced Archimedean tiling,
(b) the 1/1 step at θ = 32° where the Archimedean ordering
aligns with the direction of motion,
and (c) θ = 41° in the unlocked region just above the 1/1 step.
(d) The triangulation for the
1/1 step at θ = 32° for a sample with B/Bϕ=1.61
and FD=2.0, where most of the tiles are square.
Smectic-like ordering appears in S(k) corresponding to the
Archimedean tilings of (e) panel (a) and
(f) panel (b).
(g) S(k) for the unlocked state shown in panel (c)
has a ring structure indicating liquid ordering.
(h) At the lower field of B/Bϕ=1.61,
S(k) corresponding to panel (d) has square ordering.
Figure 3:
Delaunay triangulations of the particle
positions in the sliding state.
Bonds longer than 1.1a0 are omitted, where a0 is the lattice spacing
of a triangular lattice with the same density.
Yellow (light) polygons are triangular and blue (dark) polygons are square
or nontriangular.
For a sample with B/Bϕ=3.225
and FD=2.0 we show
(a) the 0/1 step at θ = 0 exhibiting the oriented triangles and squares
of the dynamically induced Archimedean tiling,
(b) the 1/1 step at θ = 32° where the Archimedean ordering
aligns with the direction of motion,
and (c) θ = 41° in the unlocked region just above the 1/1 step.
(d) The triangulation for the
1/1 step at θ = 32° for a sample with B/Bϕ=1.61
and FD=2.0, where most of the tiles are square.
Smectic-like ordering appears in S(k) corresponding to the
Archimedean tilings of (e) panel (a) and
(f) panel (b).
(g) S(k) for the unlocked state shown in panel (c)
has a ring structure indicating liquid ordering.
(h) At the lower field of B/Bϕ=1.61,
S(k) corresponding to panel (d) has square ordering.
|