Physical Review B 96, 094516 (2017)

Enhanced Pinning for Vortices in Hyperuniform Pinning Arrays and Emergent Hyperuniform Vortex Configurations with Quenched Disorder

Q. Le Thien1,2, D. McDermott1,3, C.J.O. Reichhardt1, and C. Reichhardt1

1Theoretical Division and Center for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA
2Department of Physics, Wabash College, Crawfordsville, Indiana 47933, USA
3Department of Physics, Pacific University, Forest Grove, Oregon 97116, USA

(Received 7 March 2017; revised manuscript received 15 August 2017; published 15 September 2017)

Disordered hyperuniformity is a state of matter exhibiting both isotropic liquid-like properties and crystalline-like properties such as minimal density fluctuations over long distances. Such states arise for jammed particle assemblies and in nonequilibrium systems. An open question is whether the properties of disordered hyperuniformity can be harnessed for technological applications. A major issue for applications of type-II superconductors is preventing the motion or depinning of magnetic vortices in order to achieve high critical currents, so there is great interest in identifying optimal pinning site geometries. Using large scale simulations, we show that a disordered hyperuniform pinning arrangement produces enhanced vortex pinning compared to an equal number of purely randomly arranged pinning sites, and that the enhancement is robust over a wide parameter range for both short and long range vortex-vortex interactions. In disordered hyperuniform arrays, pinning density fluctuations are suppressed, permitting higher pin occupancy and preventing weak links that lead to easy flow channeling. We also show that in amorphous vortex states on either random or disordered hyperuniform pinning arrays, the vortices themselves exhibit disordered hyperuniformity due to the repulsive nature of the vortex-vortex interactions.
I. INTRODUCTION
II. SYSTEM DESCRIPTION
III. ENHANCED PINNING WITH DISORDERED HYPERUNIFORM SUBSTRATES
IV. EMERGENT DISORDERED HYPERUNIFORMITY IN VORTEX SYSTEMS
V. DISORDERED HYPERUNIFORM VORTEX STATES IN THIN FILM SUPERCONDUCTORS
VI. DISCUSSION AND PROPOSED PHASE DIAGRAMS
VII. SUMMARY
REFERENCES

I.  INTRODUCTION

Disordered hyperuniformity describes amorphous systems that exhibit both liquid and crystalline properties [1,2]. The amorphous nature of these systems indicates that they are isotropic, in contrast to crystalline systems which break spatial symmetries and exhibit Bragg peaks. Disordered hyperuniform systems also show strong suppression of density fluctuations out to long length scales, a crystal-like property, where the density per unit cell is fixed at a constant value. This is in contrast to a random assembly or Poisson distribution of particles where large density variations can occur since it is possible for points to accumulate in certain regions or to have extended regions devoid of points. In 2003, Torquato and Stillinger proposed that the concept of disordered hyperuniformity can be used to describe many-body systems in which density fluctuations are suppressed out to very long wavelengths [1]. Since then, disordered hyperuniformity has been studied in a growing number of systems including jammed particle assemblies [3,4,5], block-copolymer systems [6], near nonequilibrium critical points [7,8,9], and even in certain quantum systems [10]. An open question is identifying possible applications for systems that exhibit disordered hyperuniformity. There have already been some proposals along these lines, such as the use of hyperuniformity to create photonic materials with complete band gaps [11].
Here, we show that pinning sites in a disordered hyperuniform arrangement have superior pinning properties compared to an equivalent number of randomly arranged pinning sites for magnetic vortices in a type-II superconductor over a wide range of magnetic fields, substrate strengths, and applied drives. We show that this enhancement occurs both for stiff 3D bulk vortex systems with columnar defects and for vortices in thin film superconductors. The enhancement is more pronounced in the thin films since the disordered hyperuniform arrays suppress the filamentary flow that occurs near depinning in systems with long range interactions. One of the major issues for applications of type-II superconductors is that the onset of vortex motion limits the magnitude of the current that can be carried by a sample in the superconducting state, since the vortex motion produces dissipation through a voltage response [12,13,14]. To emphasize the importance of pinning, a general rule of thumb is that doubling the critical current reduces the cost of using these materials by half [14]. There have been intense efforts directed at improving vortex pinning by adding defects to superconducting samples in order to locally suppress the superconducting order parameter, creating low energy regions that trap vortices [14,15]. Since adding defects to the sample can decrease Tc and the critical current if the defect volume density becomes too large, there is a limit to the number of pinning sites that can be added. Therefore it is important to determine the best way to spatially distribute a fixed number of pinning sites to create the highest critical current for a wide range of fields. One method is to arrange the pinning sites in crystalline lattices [16,17,18,19,20,21,22,23], diluted ordered lattices [24,25], quasiperiodic arrangements [26,27], conformal arrangements [28,29,30], or gradient arrays [31,32,33]. Typically in systems with crystalline arrangements of pinning sites, a strong enhancement of the depinning threshold compared to random pinning arrangements occurs only for matching conditions under which the number of vortices is an integer multiple of the number of pinning sites, whereas under non-matching conditions, the periodic pinning arrays have lower depinning thresholds than random arrays since the high symmetry of the array allows easy 1D vortex flow channels to form along symmetry directions of the array [19,28]. In order to achieve strong pinning for a wide range of parameters, it would be ideal to place the pinning sites in a geometry that has reduced pinning density fluctuations, similar to crystalline arrays, while simultaneously remaining isotropic in order to eliminate easy flow symmetry channeling effects. This suggests that disordered hyperuniform pinning arrangements could be ideal for enhancing the critical current.
Another question is whether amorphous assemblies of vortices in the presence of random pinning arrange themselves in a disordered hyperuniform state or a random state. Generally, vortex structures in the presence of pinning are described as either being ordered, as in a Bragg glass state where there are no dislocations in the vortex lattice [34], or as amorphous where numerous topological defects are present [34,35,36]. Due to the repulsive interaction between vortices, strong density fluctuations are highly energetically costly, which suggests that the amorphous vortex structure may be hyperuniform in nature when vortex-vortex interactions are relevant, and more random in nature when pinning or thermal effects dominate. Since disordered hyperuniform states are expected to occur for certain charged systems [2], pinned amorphous vortex systems may be ideal places to seek emergent disordered hyperuniformity. We show that disordered hyperuniform vortex states arise for vortices interacting with either disordered hyperuniform or random pinning arrays, which suggests that disordered hyperuniformity is a general feature of pinned vortex systems. There are many techniques that have been used to visualize large amorphous vortex assemblies [37,38,39,40,41,42,43,44,45], and it would be interesting to re-examine this data to see if disordered hyperuniform or random configurations occur. Additionally, there are a wide class of systems that have many similarities to amorphous vortices in the presence of pinning which may also exhibit disordered hyperuniformity, including charge-stabilized colloids [46], Wigner crystals [47], and skyrmions in chiral magnets [48,49].
This paper is organized as follows. In Section II we describe our simulation model. We primarily focus on models of bulk 3D superconducting samples in which the vortices can be represented by stiff lines. In Section III we show that the disordered hyperuniform pinning array produces an enhanced critical current as well as a reduced vortex velocity in the flowing state compared to a random pinning array with the same number of pinning sites. We then shift our attention to the structure of the vortices in the pinned state, and in Section IV we show that the vortices themselves form an emergent disordered hyperuniform structure even when the underlying pinning array is random. To our knowledge, this is the first observation of a disordered hyperuniform state in the presence of quenched disorder. In Section V we consider a model for long range interacting vortices in a 2D thin film, and show that not only is the critical current enhancement by the disordered hyperuniform pinning array robust, it is even more pronounced than in the bulk 3D samples due to the small shear modulus of the thin film system. We observe the same emergent disordered hyperuniform vortex structure in the pinned state that appeared in the bulk 3D system. Section VI contains a discussion of our results, including some schematic phase diagrams indicating the regimes in which disordered hyperuniform vortex states could be observed experimentally, as well as a demonstration that our results are robust against the addition of thermal fluctuations. A unique aspect of our results is the creation of a hyperuniform arrangement of monodisperse particles through the addition of quenched disorder. In contrast, many investigations of two-dimensional particle based systems use bidisperse particle assemblies in order to prevent crystallization.

II.  SYSTEM DESCRIPTION

The key feature of disordered hyperuniformity is the suppression of density fluctuations out to long distances. This can be characterized in reciprocal space by the behavior of the structure factor
S(k)=Nv−1⎢
⎢ 		Nv
∑
i 
 exp(−ik ·Ri)⎢
⎢ 		2
 
  (k ≠ 0),
(1)
where there are Nv particles and Ri are the positions of the particles. In hyperuniform systems, which include crystals, S(k) → 0 as |k| → 0, but unlike crystals, S(k) for disordered hyperuniform systems is isotropic and has no Bragg peaks [1,2]. In general, for a disordered hyperuniform system S(k) goes to zero as |k|α, where larger values of α indicate greater amounts of short-range order. For a random system, S(k) is isotropic but it approaches a finite value as |k| goes to zero. Hyperuniformity can also be characterized [2] using the number variance σ2(R), which is the variance of N(R), the number density or the number of points in a region defined by a d-dimensional sphere Ω(R) of radius R,
σ2(R) = 〈N2(R)〉− 〈N(R)〉2 .
(2)
For a random or Poisson placement of points in a d-dimensional region of radius R, σ2(R)  ∼ R2, while for a hyperuniform point arrangement, σ2(R)  ∼ Rd−α for α < 1, σ2(R)  ∼ Rd−1 for α > 1, and σ2(R)  ∼ Rd−1 lnR for α = 1 [50].
Fig1.png
Figure 1: The pinning site locations (open circles) for (a) a disordered hyperuniform array and (b) a random array. (c) The structure factor S(k) for the disordered hyperuniform pinning array, where the weight vanishes at small k and the system is isotropic. (d) S(k) for the random pinning array, where the system is isotropic but the weight approaches a finite value at small k. (e) S(k) vs k=|k| for the disordered hyperuniform array. The dashed line is a fit to S(k) ∝ k2. (f) S(k) vs k for the random array approaches a constant value at small k.
Fig2.png
Figure 2: The number variance σ2 vs region radius R for the pinning site configurations in Fig. 1. Red squares: disordered hyperuniform array, with the orange dashed line indicating a fit to σ2 ∝ R1.0; blue circles: random array, with the green dashed line indicating a fit to σ2 ∝ R2.0.
We consider d=2 systems in which we place Np pinning sites arranged in either a random or a disordered hyperuniform configuration as shown in Fig. 1(a,b). The pinning sites are modeled as nonoverlapping local attractive parabolic wells with radius rp. To construct the disordered hyperuniform array, we set up a square lattice of cells and place one pinning site at a randomly chosen location within each cell [1,2,50], while the random array is produced using a Poisson distribution. Figure 1(c,d) shows S(k) for the pinning configurations in Fig. 1(a,b). At small k, S(k) has constant weight for the random array but vanishing weight for the disordered hyperuniform array. In both cases S(k) is isotropic, indicating that the points are amorphous. In Fig. 1(e,f) we plot S(k) versus k for the disordered hyperuniform and random arrays, showing that S(k) goes to zero at small k for the disordered hyperuniform system as S(k) ∝ k2, indicating that α ≈ 2, while for the random array S(k) approaches a finite constant value at small k. In Fig. 2 we plot the number variance σ2 versus R for the pinning site locations from the system in Fig. 1. For the random array, σ2 ∝ R2 or σ2  ∼ Rd as expected for a Poisson process, while for the disordered hyperuniform array, σ2 ∝ R or σ2  ∼ Rd−1 as expected for a d=2 disordered hyperuniform system with α > 1.0 [2].
Within the sample we place Nv vortices modeled as point particles with a repulsion given by a pairwise Bessel function K1(r) interaction as used in previous vortex simulations [19,24,28,32]. This model represents the behavior of stiff 3D vortex lines in a bulk sample. The initial vortex positions are obtained by starting from a high temperature state and cooling to T = 0. After the initialization we apply a driving force, which experimentally corresponds to the application of an external current that creates a Lorentz force on the vortices. We wait a fixed time at each drive increment to ensure that the system has reached a steady state, and then we measure the average vortex velocity 〈V〉 = Nv−1∑i=1Nvvi ·∧x in the direction of the driving force to determine when the vortices depin and to construct velocity-force curves that are proportional to experimentally measurable current-voltage curves.
Fig3.png
Figure 3: Vortex velocity 〈V〉 vs driving force FD for a disordered hyperuniform pinning array (red, lower curves) and random pinning array (blue, upper curves) for systems with pinning density np = 0.7 and pinning strength Fp = 2.55. (a) B/Bϕ = 0.3, where Bϕ is the field at which there is one vortex per pinning site. The ratio of the depinning threshold for the disordered hyperuniform array to that of the random array is Re = 1.125. (b) At B/Bϕ = 1.0, Re = 1.8. (c) At B/Bϕ = 2.7, Re = 1.2.
To describe the vortex motion, we utilize a particle model based on the London equations. The dynamics of a single vortex i is governed by the following overdamped equation of motion:
η dRi
dt
 = Fvvi + Fvpi + FD ,
(3)
where vi = d Ri/dt is the vortex velocity, Ri is the vortex position, and η is the damping term which is set to unity. The interaction with the other vortices is repulsive and described by the term F vvi = ∑Nvj=1F0K1(Rij/λ) ∧rij where F0 = ϕ20/2πμ0λ3, ϕ0 is the elementary flux quantum, μ0 is the permittivity, Rij=|ri − rj|, ∧rij=(ri − rj)/Rij, K1 is the modified Bessel function which falls off exponentially for large Rij, and λ is the London penetration depth which we set equal to 1.0. We place a cutoff on the interactions for vortex separations Rij/λ > 6.0 for computational efficiency. At T = 0 and in the absence of pinning, the vortices form a triangular solid due to their mutually repulsive interactions. The pinning force Fvpi is produced by Np non-overlapping harmonic potential traps with a radius Rp=0.15 which can exert a maximum pinning force of Fp on a vortex. The driving term FD=FD∧x represents a Lorentz force from an externally applied current interacting with the magnetic flux carried by the vortices [26]. Our system is of size L ×L with L=36, and has periodic boundary conditions in the x and y directions. The vortex density is nv=Nv/L2 and the pinning density is np=Np/L2. In this work all forces are measured in units of F0 and lengths in units of λ. In the bulk system, for np=0.7 the pinning sites are spaced by approximately 1.2λ, so at a field B/Bϕ = 1.0, the vortices are separated by ≈ 1.2λ. These parameters fall within the same range of values used in previous simulations of vortex systems that have accurately captured the vortex pinning behavior in random [24,28,26,27], periodic [19,24,25], spin ice pinning arrays [22,23], quasi-periodic [26,27], and conformal pinning arrays [28,29]. As an example of the magnitude of magnetic fields that these length scales represent, the vortex separation mentioned above at B/Bϕ=1.0 corresponds to a field of 0.7 ϕ0/λ2. Since ϕ0=2.0678 ×10−15 T/m2, we obtain fields of 0.059T for YBCO (λ = 156 nm), 0.083T for MgB2 (λ = 132 nm), and 0.535T for Nb (λ = 52 nm).
Experimentally our system could be realized with artificial pinning arrays, in which the pinning sites could be arranged in a Poisson distribution [27] and compared to arrays with a hyperuniform pinning arrangement. Poisson pinning distributions also arise in samples containing columnar defects created using heavy ion irradiation [51,52]. Through use of a mask, it should be possible to create a hyperuniform arrangement of areas containing columnar pins, and compare this to a Poisson arrangement of areas containing columnar pins.

III.  ENHANCED PINNING WITH DISORDERED HYPERUNIFORM SUBSTRATES

Fig4.png
Figure 4: (a) The depinning force Fc vs B/Bϕ for disordered hyperuniform arrays with Fp = 2.55 (dark blue circles), 1.05 (dark green squares), and 0.53 (dark red left triangles), and for random pinning arrays with Fp = 2.55, (light blue diamonds), 1.05 (light green up triangles), and 0.53 (orange down triangles). The inset shows a blow-up of the behavior at higher fields. (b) The depinning threshold ratio Re = Fhyperc/Frandomc vs B/Bϕ for Fp = 2.55 (dark blue circles), 1.05 (light blue triangles), and 0.53 (green squares), showing that the pinning is consistently enhanced for the disordered hyperuniform pinning arrays.
In Fig. 3 we plot the vortex velocity 〈V〉 vs applied driving force FD for a system with Fp=2.55 and a pinning density of np=0.7 with Np=900 pinning sites arranged in either a disordered hyperuniform or a random array. Since the vortex density is proportional to the magnetic field, we define the matching field Bϕ as the field at which there is exactly one vortex per pinning site. The depinning threshold is defined to be the lowest value of FD for which a persistent flow of vortices occurs so that 〈V〉 > 0. At B/Bϕ = 0.3 in Fig. 3(a), the depinning threshold for the disordered hyperuniform array is Fhyperc/Fp = 0.936, while that of the random array is Frandomc/Fp=0.832. We quantify the pinning enhancement Re as the ratio of these two depinning thresholds, Re = Fhyperc/Frandomc. At B/Bϕ=0.3, Re=1.125, while for FD/Fhyperc > 1.0, the velocity response for both pinning arrays is almost the same. In general, at lower fields where the vortices are widely spaced, the vortex-vortex interactions are less relevant and the depinning threshold is dominated by the strength of the individual pinning sites, so in the extremely low field limit of a single vortex, Re = 1.0. At B/Bϕ = 1.0, Fig. 3(b) shows that the depinning threshold is larger for the disordered hyperuniform array, with Re = 1.8. Here, once both systems have depinned, the velocity response for the random array is higher than that of the disordered hyperuniform array, indicating that even within the sliding state, the disordered hyperuniform array is more effective in reducing the dissipation. For B/Bϕ = 2.7 in Fig. 3(c), there is a smaller enhancement of Re = 1.2, and above depinning, the velocity response of the disordered hyperuniform array is slightly below that of the random array. In general, at higher vortex densities the vortex-vortex interactions begin to dominate over the vortex-pin interactions, so the difference in the pinning effectiveness of the two pinning geometries is reduced.
Fig5.png
Figure 5: The depinning force Fc vs Fp for disordered hyperuniform arrays at B/Bϕ=0.6 (dark blue circles) and B/Bϕ=1.9 (dark green diamonds) and for random arrays at B/Bϕ = 0.6 (light blue squares) and B/Bϕ=1.9 (light green triangles). Inset: the depinning current ratio Re vs Fp for B/Bϕ=0.6 (red squares) and B/Bϕ=1.9 (pink circles).
In Fig. 4(a) we plot Fhyperc and Frandomc versus B/Bϕ for the system in Fig. 3 at varied pinning strengths of Fp = 2.55, 1.05, and 0.53. For all cases, Fc decreases monotonically with increasing B/Bϕ and is consistently higher in the disordered hyperuniform arrays than in the random arrays. In Fig. 4(b) the corresponding depinning threshold ratio Re versus B/Bϕ approaches Re=1.0 in the B/Bϕ=0 limit. The largest enhancement of Fc by the disordered hyperuniform arrays occurs over the range 0.5 < B/Bϕ < 2.5. In this regime, for some fields in the Fp = 2.55 system the enhancement is as large as Re=2.75. At higher values of B/Bϕ, the vortex-vortex interactions begin to dominate over the pinning interactions, and the differences in Fc between the disordered hyperuniform and random arrays are reduced.
Fig6.png
Figure 6: (a) Fraction Pv of vortices located at pinning sites vs B/Bϕ for disordered hyperuniform arrays at Fp = 2.55 (dark blue circles), 1.05 (dark green squares), and 0.53 (red diamonds), and random arrays at Fp = 2.55 (light blue up triangles), 1.05 (light green left triangles), and 0.53 (orange down triangles), showing that there is a consistently higher fraction of occupied pinning sites in the disordered hyperuniform arrays. (b) Pv vs Fp for disordered hyperuniform arrays at B/Bϕ = 1.9 (dark blue circles) and 0.6 (dark green squares) and random arrays at B/Bϕ = 1.9 (light blue diamonds) and 0.6 (light green triangles), showing a similar trend. (c) The vortex (blue filled circles) and pinning site (orange open circles) locations in a small portion of the sample for a disordered hyperuniform array at Fp = 2.55 and B/Bϕ = 1.5. (d) Vortex (blue filled circles) and pinning site (orange open circles) locations in a small portion of the sample for the random array under the same conditions showing that a higher fraction of pinning sites are unoccupied.
In Fig. 5 we plot Fhyperc and Frandomc versus pinning strength Fp at B/Bϕ = 0.6 and B/Bϕ=1.9, and show the corresponding Re vs Fp curves in the inset. The value of Re can be as large as R=2.75 for B/Bϕ = 0.6, but falls to Re=1.25 for higher Fp when the pinning begins to dominate the behavior. For B/Bϕ = 1.9, the maximum enhancement is only Re = 1.5, but the enhancement is more robust and persists up to higher values of Fp.
Fig7.png
Figure 7: (a,b,c) S(k) of the vortex positions for np = 0.7 at Fp = 0.53 (green), 1.05 (orange), and 2.55 (purple) for a random pinning array at (a) B/Bϕ = 0.6, (b) B/Bϕ=1.9, and (c) B/Bϕ=2.7. (d,e,f) S(k) of the vortex positions for np = 0.7 at the same Fp values as above for a disordered hyperuniform pinning array at (d) B/Bϕ = 0.6, (e) B/Bϕ = 1.9, and (f) B/Bϕ = 2.7. In each case k goes to zero as a power law S(k) ∝ |k|α, as indicated by the dashed lines which are all power law fits with exponent α = 2.0.
To better understand how the disordered hyperuniform arrays produce enhanced pinning, in Fig. 6(a) we plot the fraction Pv of vortices located at pinning sites versus B/Bϕ at Fp = 2.55, 1.05, and 0.53 for the random and disordered hyperuniform arrays, showing that Pv is higher for the disordered hyperuniform array than for the random array. In Fig. 6(b) we plot Pv versus Fp for samples with B/Bϕ = 1.9 and 0.6, where a similar trend appears. Figure 6(c,d) illustrates the vortex and pinning site locations in a small portion of the sample for B/Bϕ = 1.9 and Fp = 2.55. Here, there are five unoccupied pinning sites in the disordered hyperuniform array in Fig. 6(c), while there are eleven unoccupied pinning sites in the random array in Fig. 6(d). In the random array, local clumping of the pinning site positions can occur, and if a vortex is trapped by one pinning site in such a clump, its repulsive force screens the remaining pins and prevents other vortices from occupying them. The random array can also contain large spatial regions in which there are no pinning sites, and vortices located in these regions can flow relatively easily along river-like channels or weak links, depressing the value of Fc. In the disordered hyperuniform array, pinning density fluctuations are suppressed, so there is less screening of the pinning sites and a correspondingly higher pin occupation fraction, as shown in Fig. 6. In periodic pinning arrays, pinning density fluctuations are absent; however, due to the symmetry of the pinning lattice, there are easy flow directions along which vortices can form one-dimensional easy-flow channels, particularly at incommensurate fillings [32]. It may be possible to construct other types of hyperuniform arrays beyond the ones we consider here which would allow for even stronger enhancement of the pinning, or to create a pinning lattice that is hyperuniform along only one direction.

IV.  EMERGENT DISORDERED HYPERUNIFORMITY IN VORTEX SYSTEMS

Fig8.png
Figure 8: Vortex (blue filled circles) and pinning site (orange open circles) location in the entire sample at B/Bϕ = 1.9 at Fp = 2.55 for (a) a disordered hyperuniform pinning array and (b) a random pinning array. (c) Structure factor S(k) for the vortex positions in panel (a). (d) S(k) for the vortex positions in panel (b).
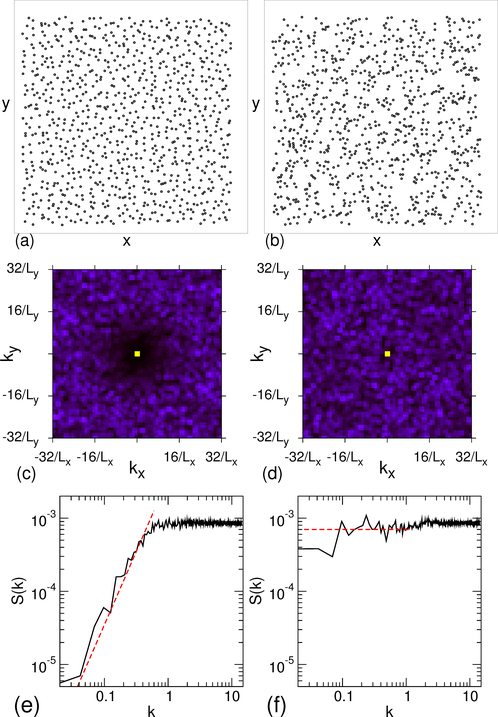
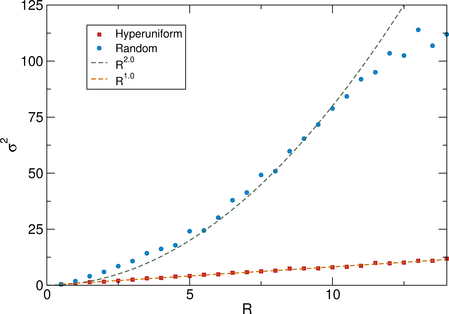
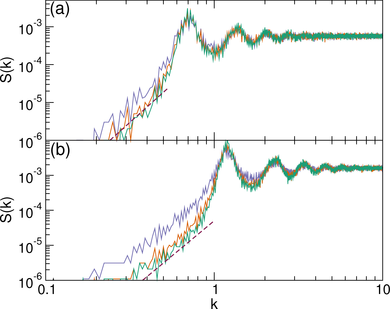
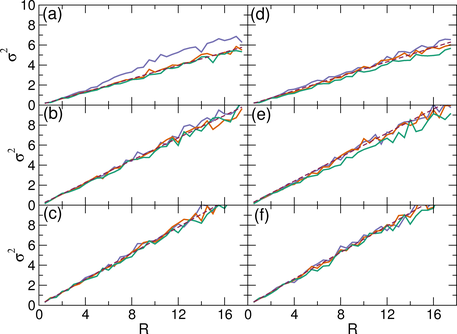
Fig9.png
Figure 9: (a,b,c) σ2 of the vortex positions vs R at Fp = 0.53 (green), 1.05 (orange) and 2.55 (purple) for the system in Fig. 7(a,b,c) with a random pinning array with np=0.7 at (a) B/Bϕ = 0.6, (b) B/Bϕ = 1.9, and (c) B/Bϕ = 2.7. (d,e,f) σ2 of the vortex positions vs R at the same Fp values as above for the system in Fig. 7(d,e,f) with a disordered hyperuniform pinning array at (d) B/Bϕ = 0.6, (e) B/Bϕ = 1.9, and (f) B/Bϕ = 2.7. The dashed brown lines in each panel are fits to σ2 ∝ Rd−1.
We next consider whether amorphous vortex configurations in the presence of random or disordered hyperuniform pinning arrays exhibit disordered hyperuniformity. As described above, disordered hyperuniform systems have two identifying characteristics in the structure factor S(k): it is isotropic, and it goes to zero as |k|α at small |k|. In Fig. 7(a,b,c) we show S(k) of the vortex configuration for a random pinning array at np = 0.7 with Fp = 0.53, 1.05, and 2.55 for B/Bϕ = 0.6, 1.9, and 2.7, while in Fig. 7(d,e,f) we plot the same quantities for vortices interacting with a disordered hyperuniform pinning array. All of the curves in Fig. 7 exhibit a power law decay with S(k) approaching zero as S(k) ∝ kα with α = 2, as indicated by the dashed lines. In each case the vortices form an amorphous structure, as shown in Fig. 8(a,b) for the disordered hyperuniform and random arrays at B/Bϕ = 1.9 and Fp = 2.55. The corresponding plots of S(k) for the vortex configurations appear in Fig. 8(c,d), and show a ring feature indicating that the vortices are arranged isotropically for both types of pinning. In Fig. 9(a,b,c) we plot σ2(R) for the vortex positions for the random pinning arrays from Fig.7(a,b,c) at Fp = 0.53, 1.05, and 2.55 for fields of B/Bϕ=0.6, 1.9, and 2.7 along with fits to σ2 ∝ Rd−1. Figure 9(d,e,f) shows σ2(R) for the vortex positions in the disordered hyperuniform arrays from Fig. 7(d,e,f) at the same values of Fp and B/Bϕ where again we find σ2 ∝ Rd−1 consistent with a disordered hyperuniform structure [2].

V.  DISORDERED HYPERUNIFORM VORTEX STATES IN THIN FILM SUPERCONDUCTORS

Up to this point we have considered vortex-vortex interactions with a Bessel function form that is exponentially screened at larger distances. Such interactions are appropriate for describing stiff 3D vortices in bulk materials; however, many experiments on nanostructured pinning arrays are performed in thin film superconductors where the vortex interaction takes the form of a long-range logarithmic Pearl potential [53]. To compare the performance of disordered hyperuniform and random pinning arrays in thin-film materials, we conduct simulations utilizing Eq. 3 but with the vortex-vortex interaction force replaced by
Fvvi = − Nv
∑
j ≠ i 
 Av∇Uv(Rij)
^
R
 
ij 
(4)
where the Pearl vortex-vortex interaction potential is U(r) = −ln(r), Av = ϕ20/8π2Λ, and Λ = λ2/t where t is the film thickness. We calculate the long-range interactions in the periodic boundary conditions with a Lekner summation technique [54,55]. This approach has previously been used to numerically examine vortex states and dynamics in random [56] and periodic pinning arrays [57,58]. We use the same number of pinning sites and vortices and the same system size as in the bulk simulations described in Section II and set Av = 1.0. Since the Pearl interaction form is appropriate for vortices within a distance of a few penetration depths of one another, the simulation would be valid for a system of order a few Pearl lengths in size.
Fig10.png
Figure 10: Vortex velocity 〈V〉 vs FD for a model of vortices in a thin-film superconductor with ln(r) vortex-vortex interaction potentials using the same parameters as in Fig. 3 with np=0.7 and Fp = 2.55. The red lower curves are for a disordered hyperuniform pinning array and the blue upper curves are for a random pinning array. (a) B/Bϕ = 0.44. (b) B/Bϕ = 0.67. (c) B/Bϕ = 0.89. In all cases there is an enhancement of the pinning for the disordered hyperuniform pinning arrays.
Fig11.png
Figure 11: (a)The depinning force Fc vs B/Bϕ for random pinning arrays (squares) and disordered hyperuniform pinning arrays (circles) with Fp=2.55 for the system in Fig. 10 with long-range vortex-vortex interactions. (b) The depinning threshold ratio Re vs B/Bϕ shows a strong enhancement of Fc in the disordered hyperuniform array. (c) Fc vs Fp for random (squares) and disordered hyperuniform (circles) pinning arrays at B/Bϕ = 0.67. (d) The corresponding Re vs Fp shows pinning enhancement in the disordered hyperuniform array.
In Fig. 10 we plot 〈V〉 versus FD for systems with B/Bϕ = 0.44, 0.67, and 0.89 at Fp = 2.55 for the random and disordered hyperuniform pinning arrays. In all cases, the disordered hyperuniform pinning substantially increases the depinning threshold with Re = 3 to 5, which is a larger enhancement than that found for vortices with the shorter-range Bessel function interactions. In Fig. 11(a) we plot Fc versus B/Bϕ for random and disordered hyperuniform pinning arrays with Fp=2.55. The corresponding Re versus B/Bϕ curve in Fig. 11(b) indicates that for low fillings Re ≈ 1.0, while at B/Bϕ = 0.89 Re reaches its maximum value of Re ≈ 7. In the thin film system, the depinning threshold falls off rapidly for B/Bϕ > 1.0 for both the random and disordered hyperuniform pinning arrays; however, even within the moving phase, the net vortex velocity is significantly lower for the disordered hyperuniform arrays than for the random arrays as long as FD/Fp < 1.0. In Fig. 11(c) we plot Fc versus Fp for the disordered hyperuniform and random pinning arrays at fixed B/Bϕ = 0.67, and in Fig. 11(d) the corresponding Re versus Fp plot shows that there is a strong enhancement of the depinning threshold for the disordered hyperuniform pinning array.
Fig12.png
Figure 12: Pinning site locations (open circles), vortex positions (red dots), and vortex trajectories (blue lines) for the thin film superconductor model from Fig. 10 at B/Bϕ = 0.67, Fp = 2.55, and FD = 0.7. (a) For a random pinning array, numerous 1D filamentary flow channels form. (b) In the disordered hyperuniform pinning array, the filamentary channels are suppressed.
Studies of Grønbech-Jensen et al. [56] on the depinning of logarithmically interacting vortices in random disorder offer insights into the origin of the larger pinning enhancement by disordered hyperuniform arrays that occurs in thin films as compared to bulk superconductors. The shear modulus C66 of the thin film vortex lattice is much lower than the compression modulus C11 since the long range interactions favor a homogeneous vortex density. As a result, near depinning there is an onset of filamentary 1D flow channels aligned with the driving direction that can form without altering the local vortex density. In a random pinning array, rare regions of low pinning density occur that serve as easy nucleation sites for filamentary flow channels that reduce the depinning threshold. In Fig. 12(a) we highlight the vortex trajectories for the random pinning array system in Fig. 10(b) with B/Bϕ = 0.67 at FD = 0.7. Numerous 1D filamentary flow channels appear. In contrast, for the same drive and filling in Fig. 12(b) in the disordered hyperuniform pinning array, far fewer flow channels can form. The flow channels are unstable in the disordered hyperuniform pinning array and channels can appear and disappear from one driving force increment to another, whereas the flow channels in the random pinning array are quite persistent and the number of flow channels increases monotonically with FD. The suppression of the filamentary flow channels in the disordered hyperuniform arrays results from to the lack of rare regions of low local pinning density. These results indicate that the enhanced pinning produced by disordered hyperuniform arrays is a general property observable in both bulk and thin film superconductors, and that the enhancement is expected to be stronger in the thin films.
Fig13.png
Figure 13: S(k) of the vortex positions in the thin film superconductor model from Fig. 10 with a random pinning array at Fp=2.55 (purple), 1.05 (orange), and 0.53 (green). (a) B/Bϕ = 0.67. (b) B/Bϕ = 1.9. As in Fig. 7, we find a power law decay S(k) ∝ |k|α indicative of disordered hyperuniformity, where the dashed lines are fits with exponent α = 4.0.
The long range nature of the thin film vortex-vortex interactions should make this system ideal for observing disordered hyperuniform vortex states. In Fig. 13(a) we plot S(k) for the thin film vortex system with a random pinning array at B/Bϕ = 0.67 for Fp = 0.53, 1.05, and 2.55. Figure 13(b) shows the same system at B/Bϕ = 1.9. The dashed lines are power law fits to S(k) ∝ |k|−α with α = 4.0, indicating a greater amount of short range order compared to the bulk Bessel function system for which α = 2.0. Overall the vortex states in the thin film system are more homogeneous than in the bulk system since the long range interactions favor a more uniform vortex density. As noted, the ln(r) interaction is valid for thin film vortices interacting within a distance of a few Pearl penetration depths. Beyond that distance, the form of the potential changes to 1/r. This is still a long range interaction that should suppress the formation of large local density fluctuations, so we expect that the system would still exhibit hyperuniformity on larger length scales. Under these conditions, the scaling of S(k) ∝ kα may change from α = 4.0 to smaller values of α, but we expect that the hyperuniform condition of α > 1 would still be met. It is likely that α would be larger in the thin film system than in the bulk system, so that the enhancement of the pinning would remain larger in the thin film samples than in bulk samples.

VI.  DISCUSSION AND PROPOSED PHASE DIAGRAMS

Fig14.png
Figure 14: (a) Schematic proposed phase diagram of temperature T vs disorder strength Fp for a system of repulsively interacting particles in the presence of quenched disorder. Between the crystalline state and a random phase with Poisson characteristics, there could be a disordered hyperuniform state (DHyper). (b) Schematic proposed modified vortex phase diagram for a high temperature superconductor as a function of magnetic field H in arbitrary units vs reduced temperature T/Tc, where Tc is the critical temperature of the material. As a function of increasing H, there is a transition from a dislocation-free Bragg glass into a disordered hyperuniform state, followed by a transition to a random glassy state with Poisson characteristics at higher fields.
In general, if Fp is large or the vortex-vortex interactions are weak, the vortex configurations are dominated by the locations of the pinning sites, so in the Poisson random pinning array, the vortices would sit in the pinning sites and themselves form a spatial Poisson distribution. The resulting structure factor of the vortex positions would approach a constant value as k → 0. In real superconductors, the vortex-vortex interaction strength is non-monotonic as a function of field and temperature, as indicated by the behavior of the bulk pinning force BJc(T,B), so the pinning energy dominates the vortex-vortex interaction energy as a critical field or critical temperature is approached. It is therefore possible that as a function of increasing field or increasing temperature, a transition could occur from a crystalline to a disordered hyperuniform vortex state, followed by a second transition to a truly random state with Poisson properties. There are already numerous experimental observations of amorphous vortex states with and without large density fluctuations at higher magnetic fields [42,43,44,45], and it would be interesting to reexamine this experimental data to determine whether the vortex configurations appear to be purely random with Poisson statistics or whether they are in fact in a disordered hyperuniform state.
In Fig. 14(a) we show a proposed generic phase diagram for repulsively interacting particle systems as a function of temperature versus the pinning strength Fp. At high temperatures or for strong disorder, the system is disordered and the particle positions are random with Poisson statistics. Between the crystalline state and the purely random state we propose that a disordered hyperuniform state exists for intermediate disorder strength.
In Fig. 14(b) we illustrate a proposed variation of the vortex phase diagram for a high temperature superconductor [34,35,36] in the presence of quenched disorder. Due to the nonmonotonic behavior of the effective vortex-vortex interactions as a function of magnetic field and temperature, there is a transition from a Bragg glass state at lower fields where the vortices are dislocation-free to a vortex glass state for increasing field or increasing temperature. We conjecture that between the Bragg glass and the random amorphous vortex glass with Poisson properties, there is a state in which the vortex arrangement is disordered with hyperuniform properties. We note that for some systems, there can also be reentrant disordered phases at lower fields where the vortices are far apart and the pinning becomes dominant again, so this reentrant region could be another place in which a crossover from a disordered hyperuniform to a Poisson random vortex arrangement could occur. Data from imaging or neutron scattering experiments could show whether the vortex configurations are disordered hyperuniform at the transition between the Bragg glass and a higher field random state with Poisson characteristics. The Bragg glass state would exhibit Bragg peaks, the disordered hyperuniform glass would have no Bragg peaks but would have a structure factor that drops to zero as a power law for small k, and the Poisson random phase would have no Bragg peaks and finite weight in S(k) at small k.
Fig15.png
Figure 15: 〈V〉 vs FD for samples with nonzero thermal fluctuations of magnitude FT=2.0. Here np=0.7, Fp=2.55, and B/Bϕ=0.67. The red lower curves are for a disordered hyperuniform pinning array and the blue upper curves are for a random pinning array. (a) Bulk vortices with short range Bessel function interactions. (b) Thin film vortices with long range ln(r) interactions. In both cases the enhancement of the pinning by the disordered hyperuniform array remains robust at finite temperatures.
To check whether the disordered hyperuniform states are robust against thermal fluctuations, we have performed finite temperature simulations for both the bulk and thin film vortex models. We represent thermal fluctuations using Langevin kicks FTi which have the properties 〈FTi〉 = 0 and 〈FTi(t)FTj(t′)〉 = 2ηkBTδijδ(t−t′). We report our results in terms of FT, the maximum amplitude of the Langevin kicks. In Fig. 15(a) we plot 〈V〉 versus FD for the bulk sample with short range vortex interactions at B/Bϕ = 0.67 and Fp = 2.55 at FT = 2.0 for random and disordered hyperuniform pinning arrays, showing that the enhancement of pinning in the disordered hyperuniform array is robust against thermal fluctuations. For these parameters, the finite depinning threshold vanishes for FT > 2.5 and the system enters a liquid state. In Fig. 15(b) we plot 〈V〉 versus FD under the same conditions but with long-range vortex interactions appropriate for a thin film sample, and find that the enhanced pinning effect in the disordered hyperuniform array is maintained at finite temperature.
Fig16.png
Figure 16: S(k) of the vortex positions in samples with random pinning arrays at B/Bϕ=1.9 and Fp=2.55 for differing levels of thermal fluctuations FT=10 (purple), 5 (orange), and 1 (green). (a) Bulk vortices with short range Bessel function interactions. Dashed lines are fits to S(k) ∝ |k|α; the upper dashed line has α = 1.25 and the lower dashed line has α = 2.25. (b) Thin film vortices with long range interactions. The upper dashed line is a power law fit with α = 2.0 and the lower dashed line is a fit with α = 4.0.
In Fig. 16(a) we plot S(k) of the vortex positions for a bulk sample with short range vortex-vortex interactions in the presence of a random pinning array at Fp = 2.55 at different temperatures of FT = 10.0, 5.0, and 1.0. At low temperatures, we find a fit of S(k) ∝ |k|α with α = 2.25, while at higher temperatures we find a similar fit with α = 1.25. As α decreases, the amount of short range order in the system decreases, so at the higher temperatures where the system is in a liquid phase, the vortex configuration is becoming more random and less hyperuniform. For temperatures above the range that we can access with our model, the system should enter a gas phase, and in this case we would expect a fit to give α = 0 indicating that the vortex configuration has become fully random. Our numerical algorithm for finite vortex interactions becomes unstable when the vortices approach each other too closely, limiting the upper temperature we can simulate. The overall behavior of S(k) as a function of temperature that we observe is consistent with our proposed 2D phase diagram in Fig. 14(a), where the system exhibits disordered hyperuniformity for finite temperature and finite quenched disorder. We find a similar trend for long range vortex interactions appropriate for thin film samples, as shown in Fig. 16(b) where we find α = 4.0 at lower temperatures and α = 2.0 at higher temperatures. The longer range interactions favor a more uniform vortex density, giving an extended region of disordered hyperuniformity.

VII.  SUMMARY

We have shown that pinning sites in a disordered hyperuniform arrangement provide enhanced pinning compared to an equivalent number of randomly placed pinning sites. In disordered hyperuniform arrays, the structure is isotropic like a liquid; however, the density fluctuations in the pinning site locations are strongly reduced out to large distances, similar to what is found in a crystal. Random arrays are also isotropic but can have strong density fluctuations of the type found in liquids. In the disordered hyperuniform pinning arrays, we find that the probability for pinning site occupation is enhanced, while weak links or easy flow channels are minimized due to the isotropic nature of the pinning arrangement. There are no symmetry directions along which easy vortex flow can occur, unlike in crystalline pinning arrays. We also show that in the presence of random or disordered hyperuniform pinning arrays, the amorphous vortex states themselves exhibit disordered hyperuniformity due to the repulsive nature of the vortex-vortex interactions, and we propose that there may be additional disordered hyperuniform phases that are distinct from random amorphous phases in the vortex phase diagram. We find that these results are robust for both short range vortex interactions appropriate for bulk samples as well as for long range vortex interactions appropriate for thin film superconductors.
Our results should be general to the wider class of systems of repulsively interacting particles in the presence of either random or disordered hyperuniform pinning arrays, including Wigner crystals, colloids, disordered charge systems, and skyrmions in chiral magnets. We note that in the course of completing this work we became aware of simulations using a Landau-Ginzburg approach to model vortices interacting with pinning sites in a disordered hyperuniform arrangement that also show an enhancement of pinning compared to random pinning arrangements [59]. Although these studies were performed on a much smaller system than we consider, they confirm that the pinning enhancement by disordered hyperuniform arrays is robust in both the London model particle-based approach we consider as well as the Landau-Ginzburg approach.

ACKNOWLEDGMENTS

We gratefully acknowledge the support of the U.S. Department of Energy through the LANL/LDRD program for this work. This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396 and through the LANL/LDRD program.

REFERENCES

[1]
S. Torquato and F.H. Stillinger, Local density fluctuations, hyperuniformity, and order metrics, Phys. Rev. E 68, 041113 (2003).
[2]
S. Torquato, Hyperuniformity and its generalizations, Phys. Rev. E 94, 022122 (2016).
[3]
C.E. Zachary, Y. Jiao, and S. Torquato, Hyperuniform long-range correlations are a signature of disordered jammed hard-particle packings, Phys. Rev. Lett. 106, 178001 (2011).
[4]
R. Dreyfus, Y. Xu, T. Still, L.A. Hough, A.G. Yodh, and S. Torquato, Diagnosing hyperuniformity in two-dimensional, disordered, jammed packings of soft spheres, Phys. Rev. E 91, 012302 (2015).
[5]
S. Atkinson, G. Zhang, A.B. Hopkins, and S. Torquato, Critical slowing down and hyperuniformity on approach to jamming, Phys. Rev. E 94, 012902 (2016).
[6]
G. Zito, G. Rusciano, G. Pesce, A. Malafronte, R. Di Girolamo, G. Ausanio, A. Vecchione, and A. Sasso, Nanoscale engineering of two-dimensional disordered hyperuniform block-copolymer assemblies, Phys. Rev. E 92, 050601 (2015).
[7]
D. Hexner and D. Levine, Hyperuniformity of critical absorbing states, Phys. Rev. Lett. 114, 110602 (2015).
[8]
J.H. Weijs, R. Jeanneret, R. Dreyfus, and D. Bartolo, Emergent hyperuniformity in periodically driven emulsions, Phys. Rev. Lett. 115, 108301 (2015).
[9]
E. Tjhung and L. Berthier, Hyperuniform density fluctuations and diverging dynamic correlations in periodically driven colloidal suspensions, Phys. Rev. Lett. 114, 148301 (2015).
[10]
S. Torquato, A. Scardicchio, and C.E. Zachary, Point processes in arbitrary dimension from Fermionic gases, random matrix theory, and number theory, J. Stat. Mech.: Theory Exp. 2008, P11019 (2008).
[11]
W. Man, M. Florescu, E.P. Williamson, Y. He, S.R. Hashemizad, B.Y.C. Leung, D.R. Liner, S. Torquato, P.M. Chaikin, and P.J. Steinhardt, Isotropic band gaps and freeform waveguides observed in hyperuniform disordered photonic solids, Proc. Natl. Acad. Sci. (USA) 110, 15886 (2013).
[12]
G. Blatter, M.V. Feigelman, V.B. Geshkenbein, A.I. Larkin, and V.M. Vinokur, Vortices in high-temperature superconductors, Rev. Mod. Phys. 66, 1125 (1994).
[13]
D. Larbalestier, A. Gurevich, D.M. Feldmann, and A. Polyanskii, High-Tc superconducting materials for electric power applications, Nature 414, 368-377 (2001).
[14]
S.R. Foltyn, L. Civale, J.L. Macmanus-Driscoll, Q.X. Jia, B. Maiorov, H. Wang, and M. Maley, Materials science challenges for high-temperature superconducting wire, Nature Mater. 6, 631-642 (2007).
[15]
B. Maiorov, S.A. Baily, H. Zhou, O. Ugurlu, J.A. Kennison, P.C. Dowden, T.G. Holesinger, S.R. Foltyn, and L. Civale, Synergetic combination of different types of defect to optimize pinning landscape using BaZrO3-doped YBa2Cu3O7, Nature Mater. 8, 398-404 (2009).
[16]
M. Baert, V.V. Metlushko, R. Jonckheere, V.V. Moshchalkov, and Y. Bruynseraede, Composite flux-line lattices stabilized in superconducting films by a regular array of artificial defects, Phys. Rev. Lett. 74, 3269 (1995).
[17]
K. Harada, O. Kamimura, H. Kasai, T. Matsuda, A. Tonomura, and V.V. Moshchalkov, Direct observation of vortex dynamics in superconducting films with regular arrays of defects, Science 274, 1167 (1996).
[18]
J.I. Martín, M. Vélez, J. Nogués, and I.K. Schuller, Flux pinning in a superconductor by an array of submicrometer magnetic dots, Phys. Rev. Lett. 79, 1929 (1997).
[19]
C. Reichhardt, C.J. Olson, and F. Nori, Commensurate and incommensurate vortex states in superconductors with periodic pinning arrays, Phys. Rev. B 57, 7937 (1998).
[20]
G.R. Berdiyorov, M.V. Milosevic, and F.M. Peeters, Novel commensurability effects in superconducting films with antidot arrays, Phys. Rev. Lett. 96, 207001 (2006).
[21]
I. Swiecicki, C. Ulysse, T. Wolf, R. Bernard, N. Bergeal, J. Briatico, G. Faini, J. Lesueur, and J.E. Villegas, Strong field-matching effects in superconducting YBa2Cu3O7−δ films with vortex energy landscapes engineered via masked ion irradiation, Phys. Rev. B 85, 224502 (2012).
[22]
A. Libál, C.J.O. Reichhardt, and C. Reichhardt, Creating artificial ice states using vortices in nanostructured superconductors, Phys. Rev. Lett. 102, 237004 (2009).
[23]
M.L. Latimer, G.R. Berdiyorov, Z.L. Xiao, F.M. Peeters, and W.K. Kwok, Realization of artificial ice systems for magnetic vortices in a superconducting MoGe thin film with patterned nanostructures, Phys. Rev. Lett. 111, 067001 (2013).
[24]
C. Reichhardt and C.J.O. Reichhardt, Commensurability effects at nonmatching fields for vortices in diluted periodic pinning arrays, Phys. Rev. B 76, 094512 (2007).
[25]
M. Kemmler, D. Bothner, K. Ilin, M. Siegel, R. Kleiner, and D. Koelle, Suppression of dissipation in Nb thin films with triangular antidot arrays by random removal of pinning sites, Phys. Rev. B 79, 184509 (2009).
[26]
V. Misko, S. Savel'ev, and F. Nori, Critical currents in quasiperiodic pinning arrays: Chains and Penrose lattices, Phys. Rev. Lett. 95, 177007 (2005).
[27]
M. Kemmler, C. Gürlich, A. Sterk, H. Pöhler, M. Neuhaus, M. Siegel, R. Kleiner, and D. Koelle, Commensurability effects in superconducting Nb films with quasiperiodic pinning arrays, Phys. Rev. Lett. 97, 147003 (2006).
[28]
D. Ray, C.J.O. Reichhardt, B. Jankó, and C. Reichhardt, Strongly enhanced pinning of magnetic vortices in type-II superconductors by conformal crystal arrays, Phys. Rev. Lett. 110, 267001 (2013).
[29]
Y.L. Wang, M.L. Latimer, Z.L. Xiao, R. Divan, L.E. Ocola, G.W. Crabtree, and W.K. Kwok, Enhancing the critical current of a superconducting film in a wide range of magnetic fields with a conformal array of nanoscale holes, Phys. Rev. B 87, 220501(R) (2013).
[30]
S. Guénon, Y.J. Rosen, A.C. Basaran, and I.K. Schuller, Highly effective superconducting vortex pinning in conformal crystals, Appl. Phys. Lett. 102, 252602 (2013).
[31]
M. Motta, F. Colauto, W.A. Ortiz, J. Fritzche, J. Cuppens, W. Gillijns, V.V. Moshchalkov, T.H. Johansen, A. Sanchez, and A.V. Silhanek, Enhanced pinning in superconducting thin films with graded pinning landscapes, Appl. Phys. Lett. 102, 212601 (2013).
[32]
D. Ray, C. Reichhardt, and C.J.O. Reichhardt, Pinning, ordering, and dynamics of vortices in conformal crystal and gradient pinning arrays, Phys. Rev. B 90, 094502 (2014).
[33]
Y.L. Wang, L.R. Thoutam, Z.L. Xiao, B. Shen, J.E. Pearson, R. Divan, L.E. Ocola, G.W. Crabtree, and W.K. Kwok, Enhancing superconducting critical current by randomness, Phys. Rev. B 93, 045111 (2016).
[34]
T. Giamarchi and P. Le Doussal, Phase diagrams of flux lattices with disorder, Phys. Rev. B 55, 6577 (1997).
[35]
H. Beidenkopf, N. Avraham, Y. Myasoedov, H. Shtrikman, E. Zeldov, B. Rosenstein, E.H. Brandt, and T. Tamegai, Equilibrium first-order melting and second-order glass transitions of the vortex matter in Bi2Sr2CaCu2O8, Phys. Rev. Lett. 95, 257004 (2005).
[36]
W.-K. Kwok, U. Welp, A. Glatz, A.E. Koshelev, K.J. Kihlstrom, and G.W. Crabtree, Vortices in high-performance high-temperature superconductors, Rep. Prog. Phys. 79, 116501 (2016).
[37]
A. Moser, H.J. Hug, I. Parashikov, B. Stiefel, O. Fritz, H. Thomas, A. Baratoff, H.-J. Güntherodt, and P. Chaudhari, Observation of single vortices condensed into a vortex-glass phase by magnetic force microscopy, Phys. Rev. Lett. 74, 1847 (1995).
[38]
P.E. Goa, H. Hauglin, M. Baziljevich, E. Il'yashenko, P.L. Gammel, and T.H. Johansen, Real-time magneto-optical imaging of vortices in superconducting NbSe2, Supercond. Sci. Technol. 14, 729 (2001).
[39]
Y. Fasano and M. Menghini, Magnetic-decoration imaging of structural transitions induced in vortex matter, Supercond. Sci. Technol. 21, 023001 (2008).
[40]
A.P. Petrovi\'c, Y. Fasano, R. Lortz, C. Senatore, A. Demuer, A.B. Antunes, A. Paré, D. Salloum, P. Gougeon, M. Potel, and Ø. Fischer, Real-space vortex glass imaging and the vortex phase diagram of SnMo6S8, Phys. Rev. Lett. 103, 257001 (2009).
[41]
O.M. Auslaender, L. Luan, E.W.J. Straver, J.E. Hoffman, N.C. Koshnick, E. Zeldov, D.A. Bonn, R. Liang, W.N. Hardy, and K.A. Moler, Mechanics of individual isolated vortices in a cuprate superconductor, Nature Phys. 5, 35-39 (2009).
[42]
C.-L. Song, Y. Yin, M. Zech, T. Williams, M. Yee, G.-F. Chen, J.-L. Luo, N.-L. Wang, E.W. Hudson, and J.E. Hoffman, Dopant clustering, electronic inhomogeneity, and vortex pinning in iron-based superconductors, Phys. Rev. B 87, 214519 (2013).
[43]
I. Guillamón, R. Córdoba, J. Sesé, J.M. De Teresa, M.R. Ibarra, S. Viera, and H. Suderow, Enhancement of long-range correlations in a 2D vortex lattice by an incommensurate 1D disorder potential, Nature Phys. 10, 851 (2014).
[44]
S.C. Ganguli, H. Singh, G. Saraswat, R. Ganguly, V. Bagwe, P. Shirage, A. Thamizhavel, and P. Raychaudhuri, Disordering of the vortex lattice through successive destruction of positional and orientational order in a weakly pinned Co0.0075NbSe2 single crystal, Sci. Rep. 5, 10613 (2015).
[45]
A. Kremen, S. Wissberg, N. Haham, E. Persky, Y. Frenkel, and B. Kalisky, Mechanical control of individual superconducting vortices, Nano Lett. 16, 1626-1630 (2016).
[46]
S. Deutschländer, T. Horn, H. Löwen, G. Maret, and P. Keim, Two-dimensional melting under quenched disorder, Phys. Rev. Lett. 111, 098301 (2013).
[47]
M.-C. Cha and H.A. Fertig, Topological defects, orientational order, and depinning of the electron solid in a random potential, Phys. Rev. B 50, 14368 (1994).
[48]
X. Yu, A. Kikkawa, D. Morikawa, K. Shibata, Y. Tokunaga, Y. Taguchi, and Y. Tokura, Variation of skyrmion forms and their stability in MnSi thin plates, Phys. Rev. B 91, 054411 (2015).
[49]
C. Reichhardt, D. Ray, and C.J.O. Reichhardt, Collective transport properties of driven skyrmions with random disorder, Phys. Rev. Lett. 114, 217202 (2015).
[50]
A. Gabrielli and S. Torquato, Voronoi and void statistics for super-homogeneous point processes, Phys. Rev. E 70, 041105 (2004).
[51]
L. Civale, A.D. Marwick, T.K. Worthington, M.A. Kirk, J.R. Thompson, L. Krusin-Elbaum, Y. Sun, J.R. Clem, and F. Holtzberg, Vortex confinement by columnar defects in YBa2Cu3O7 crystals: Enhanced pinning at high fields and temperatures, Phys. Rev. Lett. 67, 648 (1991).
[52]
S. Behler, S.H. Pan, P. Jess, A. Baratoff, H. -J. Güntherodt, F. Levy, G. Wirth, and J. Wiesner, Vortex pinning in ion-irradiated NbSe2 studied by scanning tunneling microscopy, Phys. Rev. Lett. 72, 1750 (1994).
[53]
J. Pearl, Current distribution in superconducting films carrying quantized fluxoids, App. Phys. Lett. 5, 65 (1964).
[54]
N. Grønbech-Jensen, Summation of logarithmic interactions in periodic media, Int. J. Mod. Phys. C 7, 873 (1996).
[55]
N. Grønbech-Jensen, Lekner summation of long range interactions in periodic systems, Int. J. Mod. Phys. C 8, 1287 (1997).
[56]
N. Grønbech-Jensen, A.R. Bishop, and D. Domínguez, Metastable filamentary vortex flow in thin film superconductors, Phys. Rev. Lett. 76, 2985 (1996).
[57]
C. Reichhardt, G.T. Zimányi, and N. Grønbech-Jensen, Complex dynamical flow phases and pinning in superconductors with rectangular pinning arrays, Phys. Rev. B 64, 014501 (2001).
[58]
C. Reichhardt, A.B. Kolton, D. Domínguez, and N. Grønbech-Jensen, Phase-locking of driven vortex lattices with transverse ac force and periodic pinning, Phys. Rev. B 64, 134508 (2001).
[59]
I. A. Sadovskyy, Y. L. Wang, Z.-L. Xiao, W.-K. Kwok, and A. Glatz, Effect of hexagonal patterned arrays and defect geometry on the critical current of superconducting films, Phys. Rev. B 95, 075303 (2017).


File translated from TEX by TTHgold, version 4.00.
 Back to Home