Journal of Physics: Condensed Matter 31, 07LT01 (2019)

Thermal Creep and the Skyrmion Hall Angle in Driven Skyrmion Crystals

C Reichhardt and C J O Reichhardt1

Theoretical Division and Center for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, NM 87545, United States of America

Email: cjrx@lanl.gov
Received 1 August 2018, revised 6 November 2018
Accepted for publication 9 November 2018
Published 31 December 2018
Abstract
We numerically examine thermal effects on the skyrmion Hall angle for driven skyrmions interacting with quenched disorder. We identify a creep regime in which motion occurs via intermittent jumps between pinned and flowing states. Here the skyrmion Hall angle is zero since the skyrmions have time to relax into equilibrium positions in the pinning sites, eliminating the side-jump motion induced by the Magnus force. At higher drives we find a crossover to a viscous flow regime where the skyrmion Hall angle is finite and increases with increasing drive or temperature. Our results are in agreement with recent experiments which also show a regime of finite skyrmion velocity with zero skyrmion Hall angle crossing over to a viscous flow regime with a skyrmion Hall angle that increases with drive.
Keywords: skyrmions, thermal creep, Magnus force
Simulation
Results
Summary
References
A wide range of systems with quenched disorder exhibit depinning phenomena under an external drive [1,2], including sliding charge density waves [3], vortices in type-II superconductors [4], colloids [5,6] and magnetic domain walls [7]. At zero temperature, these systems have a well defined depinning threshold Fc below which motion does not occur, while at finite temperature, a finite velocity arises at much lower drives due to thermal creep effects [1]. Another system that exhibits depinning phenomena is skyrmions in chiral magnets [8,9,10]. Skyrmions are topological particle-like magnetic objects that can form lattices and be driven by an applied current or by other methods [8,11,12]. Skyrmion velocity-force relations can be obtained by transport measures [9,13] and direct imaging [14,15,16,17]. The topology of the skyrmions makes them unique among systems that exhibit depinning since the skyrmion dynamics is strongly influenced by the Magnus force, which generates a velocity component perpendicular to the forces experienced by the skyrmion [8].
One consequence of the Magnus force is that skyrmions move at an angle, called the skyrmion Hall angle θsk, with respect to an external driving force [8,16,17,18]. The intrinsic value of θsk is determined by the ratio of the Magnus term to the damping term, and in the absence of quenched disorder, θsk is a constant. Particle-based simulations of moving skyrmions interacting with quenched disorder have shown that θsk can vary, starting at θsk=0 at depinning, increasing with increasing velocity, and saturating to the defect-free intrinsic value at higher drives [19,20,21,22]. This effect arises due to the Magnus-induced side jump experienced by the skyrmions when they move through a pinning site [20,23]. Under rapid skyrmion motion, the magnitude of the side jumps is reduced since the skyrmion does not have time to respond fully to the pinning potential before exiting the pinning site. Continuum-based simulations reveal a similar drive dependence of θsk when disorder is present, with θsk remaining constant in the absence of disorder [24,25]. In imaging experiments of skyrmions under an external drive, θsk=0 at low drives just above depinning, but as the drive increases, θsk increases linearly until it reaches a saturation at high drives close to the predicted intrinsic value [16]. In other experiments which show a similar drive dependence of θsk, it was argued that in addition to the pinning interactions, excitation of internal modes of the skyrmions or a change in skyrmion size with driving can modify the skyrmion Hall angle [17]. In more recent work it was claimed that both of these effects contribute to changes in θsk [26]. Far less is known about how thermal creep affects skyrmion motion or the value of θsk. Thermal effects are relevant since many materials support skyrmions at room temperature [14,15,16,18,27,28]. Additionally, in recent experiments, thermally induced Brownian motion of skyrmions has been observed directly in the absence of an external drive [29].
In this work we examine the thermal creep of skyrmions and its effect on θsk using a particle-based skyrmion model. Thermal motion is most significant near the depinning threshold where the drive is small, in a regime where the effect of the skyrmion shape on θsk, which has been proposed to be important at high drives [17], is minimal. We find that the depinning threshold decreases with increasing temperature and that a creep regime appears which is characterized by skyrmions jumping or even avalanching between pinned and moving states. Within the creep regime, θsk = 0, while at higher drives there is a crossover to viscous flow where the skyrmions are always moving and the value of θsk becomes finite and increases with drive. We note that recent particle-based simulations have examined thermal effects in skyrmions, but these studies focused on the aging dynamics in the absence of a drive [30].
Simulation
We consider a two-dimensional system of rigid skyrmions with periodic boundary conditions in the x- and y-directions. The skyrmion dynamics are modeled using a modified version of the Thiele equation [19,20,21,31], and we include Langevin dynamics that are similar to those employed previously to model thermal relaxation effects in skyrmions [30]. The equation of motion of skyrmion i is αd vi + αm ∧z ×vi = Fssi + Fpi + FD + FTi, where vi = d ri/dt is the skyrmion velocity and αd and αm are the damping and Magnus terms, respectively. The intrinsic skyrmion Hall angle is given by θinsk = tan−1(αm/αd). We fix αm/αd=1.0 so that θinsk=45°, which is close to the value in recent experiments [16,17]. The skyrmion-skyrmion interaction force Fiss = ∑Nj ≠ iK1(rij)∧rij, where K1 is the modified Bessel function, rij = |ri − rj| is the distance between skyrmions i and j, ∧rij=(ri−rj)/rij, and N is the number of skyrmions in the sample [19,31,32]. The pinning force Fspi = ∑j=1Np(Fp/rp)(ri −rpj)Θ(rp −|ri − rpj|) arises from randomly placed non-overlapping parabolic traps of radius rp = 0.15 at locations rpj that can exert a maximum pinning force of Fp=0.03 on a skyrmion. Here Θ is the Heaviside step function. The driving force from an applied current is FD = FD∧x, and we measure the average velocity per skyrmion both parallel, 〈V||〉 = N−1∑Ni=1 vi ·∧x, and perpendicular, 〈V⊥〉 = N−1∑Ni=1 vi ·∧y, to the drive. The skyrmion Hall angle is given by θsk=tan−1(〈V⊥〉/〈V||〉). The stochastic thermal force FTi has the properties 〈FTi〉 = 0 and 〈FTi(t)FTj(t′)〉 = 2ηkBTδijδ(t −t′). Here we set η = 1.0 and kB = 1.0. We use a skyrmion density of ns=N/L2=0.16, where the sample is of size L ×L with L=36. We fix the pinning density at np=Np/L2=0.2. We have considered several different system sizes and find the same general features in each case; however, with smaller systems, longer simulation times are required to obtain the velocity averages.
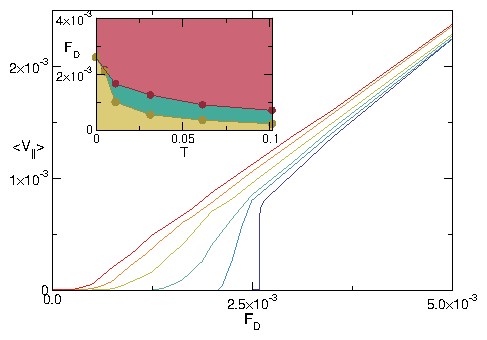
Fig1.png
Figure 1: The time average skyrmion velocity in the direction parallel to the drive, 〈V||〉, vs FD at temperatures T = 0.0 (dark blue), 0.005 (light blue), 0.01125 (dark green), 0.03125 (light green), 0.06125 (orange), and 0.1025 (red). As T increases, there is a decrease in the depinning threshold Fc and the behavior of 〈V||〉 becomes increasingly nonlinear. Inset: Dynamic phase diagram as a function of FD vs T highlighting the pinned (yellow), creep (green), and viscous flow (pink) regimes.
Results
In Fig. 1 we plot 〈V||〉 versus FD for temperatures ranging from T=0 to T=0.1025. At T = 0, there is a sharp depinning threshold at a critical depinning force of Fc = 2.6 ×10−3. As T increases, Fc decreases and the regime of nonlinear behavior of 〈V||〉 grows in extent. We measure the evolution of θsk at each temperature as a function of drive. Previous work at T = 0 showed that θsk is zero only in the pinned phase, and that θsk increases with increasing FD for FD/Fc > 1.0 [20,21,22]. At finite temperature we find an extended creep regime in which 〈V||〉 > 0 while 〈V⊥〉 = 0, giving θsk = 0 even though the skyrmion velocity is finite. Within the creep regime, the skyrmion motion is intermittent and consists of jumps between moving and pinned states. At higher drives, the creep regime transitions into a viscous flow phase in which the skyrmions are always in motion and θsk increases with FD. Based on measurements of 〈V||〉, 〈V⊥〉, θsk, and histograms of the skyrmion velocities, we construct a dynamic phase diagram as a function of FD versus T highlighting the pinned phase with 〈V||〉 = 〈V⊥〉 = 0, the creep phase with 〈V||〉 > 0 and 〈V⊥〉 = 0, and the viscous flow regime with 〈V||〉 > 0 and 〈V⊥〉 > 0, as shown in the inset of Fig. 1.
Fig2.png
Figure 2: (a) θsk vs FD at T = 0.06125. (b) 〈V||〉 (blue squares) and 〈V⊥〉 (red circles) vs FD in the same system. Here there is a pinned phase, a creep phase in which θsk is close to zero, and a flowing phase.
In Fig. 2(a) we plot θsk versus FD at T=0.06125, and in Fig. 2(b) we show the corresponding 〈V||〉 and 〈V⊥〉 versus FD curves. In the pinned phase, both 〈V||〉 and 〈V⊥〉 are zero, while in the creep regime, 〈V||〉 is finite but 〈V⊥〉 is zero or nearly zero, so that θsk is zero or close to zero. In the flow regime, both velocity components increase and θsk rises from zero. When the system first enters the flow regime, the increase in θsk with FD is nonlinear, but there is a crossover to a linear increase in θsk at higher drives. Above the range of drives illustrated in Fig. 2, θsk saturates to the intrinsic value of θskin=45°. The pinned, creep, and flow behavior of 〈V||〉, 〈V⊥〉, and θsk is very similar to the observations in imaging experiments of the room temperature motion of skyrmions [16]. In Fig. 3(a) we show the skyrmion positions and trajectories for the system in Fig. 2 in the creep regime at T=0.06125 and FD = 7.5×10−4, where the skyrmions move in the direction of drive. The trajectories are obtained over a time periodic during which the skyrmions move a distance of approximately 1.5 to 2 lattice constants. The trajectories show similar features for longer times but the plots become more difficult to visualize. At the same temperature but at a higher drive of FD=3.5×10−3 in Fig. 3(b), the skyrmions are in the flow regime and move at an angle of θsk=35° with respect to the drive.
Fig3.png
Figure 3: The skyrmion positions (dots) and trajectories (lines) in the entire sample for the system in Fig. 2 at T = 0.06125. (a) The creep phase at FD = 7.5×10−4, where θsk = 0 and the skyrmions move in the direction of drive. (b) The flow phase at FD = 3.5 ×10−3, where θsk = 35°.
Fig4.png
Figure 4: (a) Time series of V||(t) in units of 107 simulation time steps in the creep regime at FD = 7.5×10−4 and T = 0.06125. (b) The corresponding velocity histogram P(V||). (c) V||(t) and (d) P(V||) in the flow regime at FD = 3.5×10−3 and T=0.06125, where 〈V||〉 > 0 and 〈V⊥〉 > 0. (e) V||(t) in the creep regime at FD = 1.5×10−3 and T = 0.01125, where motion occurs in the form of avalanches. (f) The corresponding histogram P(V||), where the dashed line is a power law fit to P(V||) ∝ V||−α with α = 1.5.
The skyrmion motion within the creep phase has a stop-start character, where a skyrmion that is trapped by a pin escapes from the pin and undergoes a brief interval of motion before becoming trapped by an adjacent pin. While trapped, the skyrmion spirals toward the equilibrium location in the pinning site at which the pinning and driving forces are exactly balanced. In Fig. 4(a,d) we plot a velocity time series V||(t) and corresponding velocity histogram P(V||) in the creep regime at FD = 7.5×10−4 and T = 0.06125. There is a peak in P(V||) at V||=0, indicating that the skyrmions spend the largest portion of their time trapped in pinning sites. The velocity distribution in Fig. 4(d) is strongly non-Gaussian with a large linear fall off at the higher velocities. This is a result of the avalanche-like nature of the flow in the creep regime, observable in the time series of Fig. 4(a) where the skyrmions spend more time pinned than moving. In the flow regime, shown in Fig. 4(c,d) at FD = 3.5×10−3 and T = 0.06125, the skyrmions are constantly flowing and V|| > 0 at all times.
In the creep regime, θsk = 0° because the Magnus force is a dynamical quantity that can act only when the skyrmions are driven out of equilibrium. If there is sufficient time between jumps of the skyrmion from one pinning site to another, the skyrmion gradually spirals to a position in the pinning site where the pinning and drive forces are balanced. The location of this point is independent of the Magnus term, so over long times, a skyrmion in the strictly overdamped limit of αm = 0 settles into the same position as a skyrmion with αm > 0. On the other hand, if the skyrmions are continuously moving over the pinning sites, they experience a side jump motion generated by the Magnus force that pushes them away from the equilibrium force balance point of the pin, producing a finite value of θsk with a magnitude that depends on the strength of the Magnus force. As FD increases and the skyrmions move faster, the perturbation of the Magnus force by the pinning is reduced and θsk increases until it reaches the intrinsic value θsk=θskin. For increasing temperature T at fixed FD, thermal fluctuations smear out the effectiveness of the pinning, permitting the skyrmions to move continuously and causing θsk to increase.
If the temperature is lowered, within the creep regime the skyrmions spend an even larger fraction of their time trapped in pinning sites, the motion becomes increasingly intermittent, and avalanches dominate the behavior, as illustrated in the plot of V||(t) in Fig. 4(e) at FD = 1.5×10−3 and T = 0.01125. In Fig. 4(f) we show P(V||) in the avalanche regime on a log-log scale, where the dashed line is a power law fit to P(V||) ∝ V||−α with α = 1.5. In previous work, we examined the avalanche behavior just at the depinning threshold for a T=0 system, and found that various quantities such as the avalanche size and duration are power law distributed with exponents similar to that in Fig. 4(f) [32]. Here we find that under finite temperature in the creep regime, the thermal fluctuations lower Fc but the system can still exhibit critical behavior near the depinning threshold. These results indicate that in certain cases, thermally induced skyrmion avalanches can be realized with a fixed current.
Fig5.png
Figure 5: (a) 〈V||〉 (blue squares) and 〈V⊥〉 (red circles) vs T at FD = 1.5 ×10−3. (b) The corresponding θsk vs T. Yellow shading indicates the pinned regime, green shading is the creep state, and the unshaded area is in the flowing state. (c) 〈V||〉 (blue squares) and 〈V⊥〉 (red circles) vs T for the same system in the flowing state at FD = 3.5 ×10−3. (d) The corresponding θsk vs T curve shows a linear increase in θsk with increasing T up to the intrinsic value of θskin=45°.
In Fig. 5 we illustrate the temperature dependence of θsk at a fixed FD in two regimes: FD > Fc where the skyrmions are always moving, and FD < Fc where the skyrmions spend most of their time pinned. In Fig. 5(a) we plot 〈V||〉 and 〈V⊥〉 versus T at FD = 1.5 ×10−3, a drive that is lower than the T = 0 depinning threshold of Fc=2.6 ×10−3, while in Fig. 5(b) we plot the corresponding θsk versus T. We find a pinned state for T > 0.00725 and a creep state for 0.00725 ≤ T < 0.02. For T ≥ 0.02, the system is in a flowing phase and θsk increases with increasing T. In Fig. 5(c) we show 〈V||〉 and 〈V⊥〉 versus T at FD = 3.5 ×10−3, a drive that is higher than the T=0 value of Fc, and in Fig. 5(d) we plot the corresponding θsk versus T. At this drive, the skyrmions are in the flowing state for all values of T. The skyrmion Hall angle θsk=31° at T=0 and increases roughly linearly with increasing temperature before saturating at the intrinsic value of θskin=45° at high temperatures. This indicates that a temperature dependence of θsk persists even in the viscous flow phase. We note that in the absence of pinning, θsk is independent of both FD and T within the particle model. In continuum simulations performed without pinning, θsk was also shown to be independent of the drive amplitude [24].
Summary
We have examined the effect of temperature on skyrmion creep and motion using a particle based model. As temperature increases, we find that the depinning threshold drops and a nonlinear creep regime appears at low drives. Within the creep regime, the skyrmion Hall angle is zero and the skyrmions spend most of their time trapped in pinning sites, making occasional hops from one pinning site to another. While trapped, the skyrmions have enough time to spiral to the equilibrium position in the pin at which the drive and pinning forces are balanced, eliminating the Magnus-induced side-jump motion that would give a finite value for the skyrmion Hall angle. In the flowing regime, the skyrmions are always moving and the skyrmion Hall angle increases linearly with increasing drive. At low temperatures in the creep regime, we find that skyrmion motion occurs in the form of avalanches, and that the skyrmion velocities are power law distributed. The effect of temperature on the skyrmion Hall angle is most pronounced at small drives where thermally-induced depinning occurs; however, even within the flowing phase, the skyrmion Hall angle increases with increasing temperature.
Acknowledgments
We gratefully acknowledge the support of the U.S. Department of Energy through the LANL/LDRD program for this work. This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396.
ORCID iDs
C J O Reichhardt https://orcid.org/0000-0002-3487-5089
References
[1]
Fisher D S 1998 Collective transport in random media: From superconductors to earthquakes Phys. Rep. 301 113
[2]
Reichhardt C and Reichhardt C J O 2017 Depinning and nonequilibrium dynamic phases of particle assemblies driven over random and ordered substrates: A review, Rep. Prog. Phys. 80 026501
[3]
Grüner G 1988 The dynamics of charge-density waves, Rev. Mod. Phys. 60 1129
[4]
Blatter G, Feigel'man M V, Geshkenbein V B, Larkin A I and Vinokur V M 1994 Vortices in high-temperature superconductors Rev. Mod. Phys. 66 1125
[5]
Reichhardt C and Olson C J 2002 Colloidal dynamics on disordered substrates Phys. Rev. Lett. 89 078301
[6]
Bohlein T, Mikhael J and Bechinger C 2012 Observation of kinks and antikinks in colloidal monolayers driven across ordered surfaces Nat. Mater. 11 126
[7]
Metaxas P J, Jamet J P, Mougin A, Cormier M, Ferré J, Baltz V, Rodmacq B, Dieny B and Stamps R L 2007 Creep and flow regimes of magnetic domain-wall motion in ultrathin Pt/Co/Pt Films with perpendicular anisotropy Phys. Rev. Lett. 99 217208
[8]
Nagaosa N and Tokura Y 2013 Topological properties and dynamics of magnetic skyrmions Nat. Nanotechnol. 8 899
[9]
Schulz T, Ritz R, Bauer A, Halder M, Wagner M, Franz C, Pfleiderer C, Everschor K, Garst M and Rosch A 2012 Emergent electrodynamics of skyrmions in a chiral magnet Nat. Phys. 8 301
[10]
Iwasaki J, Mochizuki M and Nagaosa N 2013 Universal current-velocity relation of skyrmion motion in chiral magnets Nat. Commun. 4 1463
[11]
Mühlbauer S, Binz B, Jonietz F, Pfleiderer C, Rosch A, Neubauer A, Georgii R and Böni P 2009 Skyrmion lattice in a chiral magnet Science 323 915
[12]
Yu X Z, Onose Y, Kanazawa N, Park J H, Han J H, Matsui Y, Nagaosa N and Tokura Y 2010 Real-space observation of a two-dimensional skyrmion crystal Nature (London) 465 901
[13]
Liang D, DeGrave J P, Stolt M J, Tokura Y and Jin S 2015 Current-driven dynamics of skyrmions stabilized in MnSi nanowires revealed by topological Hall effect Nat. Commun. 6 8217
[14]
Jiang W, Upadhyaya P, Zhang W, Yu G, Jungfleisch M B, Fradin F Y, Pearson J E, Tserknovnyak Y, Wang K L, Heinonen O, te Velthuis S G E and Hoffmann A 2015 Blowing magnetic skyrmion bubbles Science 349 283
[15]
Woo S, Litzius K, Krüger B, Im M-Y, Caretta L, Richter K, Mann M, Krone A, Reeve R M, Weigand M, Agrawal P, Lemesh I, Mawass M-A, Fischer P, Kläui M and Beach G S D 2016 Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets Nat. Mater. 15 501
[16]
Jiang W, Zhang X, Yu G, Zhang W, Wang X, Jungfleisch M B, Pearson J E, Cheng X, Heinonen O, Wang K L, Zhou Y, Hoffmann A and te Velthuis S G E 2017 Direct observation of the skyrmion Hall effect Nat. Phys. 13 162
[17]
Litzius K, Lemesh I, Krüger B, Bassirian P, Caretta L, Richter K, Büttner F, Sato K, Tretiakov O A, Förster J, Reeve R M, Weigand M, Bykova I, Stoll H, Schütz G, Beach G S D and Kläui M 2017 Skyrmion Hall effect revealed by direct time-resolved X-ray microscopy Nat. Phys. 13 170
[18]
Tolley R, Montoya S A and Fullerton E E 2018 Room-temperature observation and current control of skyrmions in Pt/Co/Os/Pt thin films Phys. Rev. Materials 2 044404
[19]
Reichhardt C, Ray D and Reichhardt C J O 2015 Collective transport properties of driven skyrmions with random disorder Phys. Rev. Lett. 114 217202
[20]
Reichhardt C, Ray D and Reichhardt C J O 2015 Quantized transport for a skyrmion moving on a two-dimensional periodic substrate Phys. Rev. B 91 104426
[21]
Reichhardt C and Reichhardt C J O 2016 Noise fluctuations and drive dependence of the skyrmion Hall effect in disordered systems New J. Phys. 18 095005
[22]
Díaz S A, Reichhardt C J O, Arovas D P, Saxena A and Reichhardt C 2017 Fluctuations and noise signatures of driven magnetic skyrmions Phys. Rev. B 96 085106
[23]
Müller J and Rosch A 2015 Capturing of a magnetic skyrmion with a hole Phys. Rev. B 91 054410
[24]
Legrand W, Maccariello D, Reyren N, Garcia K, Moutafis C, Moreau-Luchaire C, Collin S, Bouzehouane K, Cros V and Fert A 2017 Room-temperature current-induced generation and motion of sub-100 nm skyrmions Nano Lett. 17 2703
[25]
Kim J-V and Yoo M-W 2017 Current-driven skyrmion dynamics in disordered films Appl. Phys. Lett. 110 132404
[26]
Litzius K, Bassirian P, Leliaert J, Kromin S, Zazvorka J, Lemesh I, Kerber N, Churikova A, Heinze D, Keil N, Weigand M, Schütz G, Beach G S D and Kläui M (to be published)
[27]
Tokunaga Y, Yu X Z, White J S, Rønnow H M, Morikawa D, Taguchi Y and Tokura Y 2015 A new class of chiral materials hosting magnetic skyrmions beyond room temperature Nat. Commun. 6 7638
[28]
Soumyanarayanan A, Raju M, Gonzalez-Oyarce A L, Tan A K C, Im M-Y, Petrovi\'c A P, Ho P, Khoo K H, Tran M, Gan C K, Ernult F and Panagopoulos C 2017 Tunable room-temperature magnetic skyrmions in Ir/Fe/Co/Pt multilayers Nat. Mater. 16 898
[29]
Zázvorka J, Jakobs F, Heinze D, Keil N, Kromin S, Jaiswal S, Litzius K, Jakob G, Virnau P, Pinna D, Everschor-Sitte K, Donges A, Nowak U and Kläui M J. Zázvorka, F. Jakobs, D. Heinze, N. Keil, S. Kromin, S. Jaiswal, K. Litzius, G. Jakob, P. Virnau, D. Pinna, K. Everschor-Sitte, A. Donges, U. Nowak, and M. Kläui, Thermal skyrmion diffusion applied in probabilistic computing (arXiv:1805.05924)
[30]
Brown B L, Täuber U C and Pleimling M 2018 Effect of the Magnus force on skyrmion relaxation dynamics Phys. Rev. B 97 020405(R)
[31]
Lin S-Z, Reichhardt C, Batista C D and Saxena A 2013 Particle model for skyrmions in metallic chiral magnets: Dynamics, pinning, and creep Phys. Rev. B 87 214419
[32]
Díaz S A, Reichhardt C, Arovas D P, Saxena A and Reichhardt C J O 2018 Avalanches and criticality in driven magnetic skyrmions Phys. Rev. Lett. 120 117203


File translated from TEX by TTHgold, version 4.00.
 Back to Home