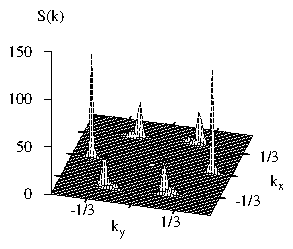
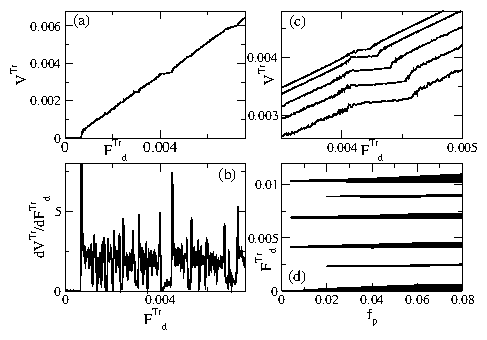
 Figure 1:
(a) The transverse velocity
VTr vs the transverse applied force FTrd
for a vortex lattice moving over random disorder
of strength fp=0.06f0
with fixed longitudinal driving force FLd=0.012f0.
(b) dVTr/dFTrd vs FTrd for the same system.
(c) VTr vs FTrd showing the evolution of the
(1,2) step for fp = 0.02, 0.04, 0.06, and 0.08f0,
from top to bottom.
(d) Step widths ws in FTrd vs fp
for the (0,0), (1,3), (1,2), (3,4), (3,3)
and (4,4) steps, from bottom to top.
Figure 1:
(a) The transverse velocity
VTr vs the transverse applied force FTrd
for a vortex lattice moving over random disorder
of strength fp=0.06f0
with fixed longitudinal driving force FLd=0.012f0.
(b) dVTr/dFTrd vs FTrd for the same system.
(c) VTr vs FTrd showing the evolution of the
(1,2) step for fp = 0.02, 0.04, 0.06, and 0.08f0,
from top to bottom.
(d) Step widths ws in FTrd vs fp
for the (0,0), (1,3), (1,2), (3,4), (3,3)
and (4,4) steps, from bottom to top.
|