Physical Review E 95, 032606 (2017)

Dynamic Phases of Active Matter Systems with Quenched Disorder

Cs. Sándor1,2, A. Libál1,2, C. Reichhardt2 and C. J. Olson Reichhardt2

1Faculty of Mathematics and Computer Science, Babes-Bolyai University, Cluj 400084, Romania 2Theoretical Division and Center for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA

(Received 24 October 2016; published 16 March 2017)

Depinning and nonequilibrium transitions within sliding states in systems driven over quenched disorder arise across a wide spectrum of size scales ranging from atomic friction at the nanoscale, flux motion in type-II superconductors at the mesoscale, colloidal motion in disordered media at the microscale, and plate tectonics at geological length scales. Here we show that active matter or self-propelled particles interacting with quenched disorder under an external drive represents a new class of system that can also exhibit pinning-depinning phenomena, plastic flow phases, and nonequilibrium sliding transitions that are correlated with distinct morphologies and velocity-force curve signatures. When interactions with the substrate are strong, a homogeneous pinned liquid phase forms that depins plastically into a uniform disordered phase and then dynamically transitions first into a moving stripe coexisting with a pinned liquid and then into a moving phase separated state at higher drives. We numerically map the resulting dynamical phase diagrams as a function of external drive, substrate interaction strength, and self-propulsion correlation length. These phases can be observed for active matter moving through random disorder. Our results indicate that intrinsically nonequilibrium systems can exhibit additional nonequilibrium transitions when subjected to an external drive.
I. INTRODUCTION
II. SIMULATION
III. DYNAMIC PHASES AND TRANSPORT ON PINNING SITES
A. Changing disk density and pinning strength
B. Changing run length and pinning density
IV. DYNAMICS IN OBSTACLE ARRAYS
V. SUMMARY
REFERENCES


I.  INTRODUCTION

Depinning phenomena and dynamic phases of collective transport through quenched disorder [1,2] arise in a wide range of condensed matter systems including flux lines in superconductors [3,4,5,6,7,8,9], sliding charge density waves [10], moving electron crystals [11,12], magnetic skyrmions [13,14], and driven pattern forming systems such as electronic states with competing interactions [15]. In materials science systems such dynamics are relevant to sliding friction [16], dislocation motion [17], yielding transitions [18,19], and models of fault lines and earthquakes [20,21]. In soft matter, similar dynamics occur in the depinning of contact lines [22,23], driven colloidal motion on disordered substrates [24,25,26], or sliding of incommensurate colloidal structures on ordered substrates [27,28]. Typically, these systems are in the pinned state at small external drives, and as the drive increases, a transition to a moving state occurs at a specific critical value of the external force [1,2]. At higher drives, distinct types of sliding motions can appear along with transitions between different dynamic states that can be deduced from features in the velocity-force curves. The flow can be plastic or disordered [1,2,3,4,5,8], with the particles moving through riverlike channels[24,25,26], or elastic, where the particles maintain the same neighbors while moving [1,3,24]. Transitions from disordered to more ordered or coherent flow can occur [3,4,5,6,8,9], such as from plastic flow to a moving smectic state [6,7,8,9]. Such transitions are associated with changes in the moving structure morphologies, the density of topological defects [4,8,9,14,24], and the noise fluctuations [5,8].
In all of the systems mentioned above, an external driving force produces a nonequilibrium condition. Other types of nonequilibrium systems that involve no external driving force include self-propelled or active matter systems. These may be biological systems, such as swimming bacteria, or artificial swimmers, such as self-propelled colloidal systems, each of which can exhibit distinct nonequilibrium phases as a function of the activity or particle density [29,30]. Many types of active matter systems can be effectively modeled as a collection of sterically interacting disks undergoing driven Brownian diffusion [31,32,33,34,35] or run-and-tumble dynamics [35,36,37,38]. These disks can form uniform liquid states as well as phase separated states in which dense disk clusters are separated by a low density disk gas. An open question is whether such systems would exhibit depinning transitions and different types of sliding states if an external drive were applied when the disks are coupled to a random substrate, as the driven dynamics of particles interacting with obstacles generally are distinct from those of particles on random pinning substrates. Previous studies of active matter systems driven through obstacle arrays showed that the average drift mobility varies non-monotonically with increasing activity, dropping when the system forms a phase-separated clump state [38]. Other studies of active matter involving swarming or Vicsek flocking models moving over disordered substrates in the absence of an external drive showed that there can be an optimal noise at which flocking occurs [39] as well as transitions from flocking to non-flocking behavior [40].
Here we use large scale GPU-based computer simulations to characterize the different states of run-and-tumble disks driven over a random pinning substrate, and show that a rich variety of distinct dynamical phases are possible that can be identified by the morphologies of the moving structures as well as by features in bulk transport properties. Despite the additional complexity introduced by the self-propulsion, we find several generic features in the dynamic phase diagrams that are similar to those observed for non-active driven systems such as superconducting vortex lattices, including a disorder-order transition at higher drives. In the limit of no quenched disorder, we find a cluster or phase-separated state, while in the presence of strong quenched disorder, the system forms a uniform pinned liquid state which undergoes plastic depinning as the drive is increased, followed at higher drives by a transition to a stripe state coexisting with the pinned liquid state. At even higher drives, there is a transition to a more fully phase separated state. We also find strong differences in the dynamic phases for pinning arrays compared to those observed in obstacle arrays, where only a limited number of dynamic phases occur.
The organization of this paper is as follows. In Section III we describe the dynamic phases that arise for active run-and-tumble disks driven over pinning arrays. The five generic phases that emerge for high activity, shown in Section III A, are the pinned phase I, the disordered plastic flow phase II, the moving cluster-stripe phase III coexisting with pinned disks, and two phases in which all of the disks are moving: the moving cluster or phase separated phase IV and the moving disordered or liquid phase V. We demonstrate the evolution of these phases as the pinning strength is varied, and find that the extent of the pinned phase, the plastic disordered flow phase, and the stripe phase increase with increasing pinning strength. In the limit of zero drive we observe a transition from a phase separated state to a disordered pinned state as the pinning force increases. The different states can be identified by analyzing changes in the size of the clusters, the fraction of disks with six neighbors, and the velocity-force curves. We compare the evolution of the dynamic phases with pinning strength to that observed for vortices in type-II superconductors and other driven particle systems. In Section III B we explore the effects on the dynamic phases of changing the activity from the non-active or Brownian limit to the highly active limit, and find that there is a critical activity level or run length below which phases III and IV do not occur. In Section IV we show how the driven phases change when the pinning sites are replaced by obstacles. There is still a transition from a phase separated to a disordered phase as a function of obstacle density in the zero drive limit; however, we find no dynamical phase transitions within the moving phase, and the cluster size and transport curves show only smooth changes with increasing obstacle density. We provide a summary of our results in Section V.

II.  SIMULATION

We perform a simulation of N = 5000 to N = 24000 run-and-tumble disks in a system with periodic boundary conditions of size L ×L with L=300. The disks have a short range repulsive interaction modeled as a harmonic spring force Finter=Θ(d−2R)k(d−2R)∧d, where d is the distance between the centers of the disks, ∧d is the displacement vector between the disk centers, k=20.0 is the spring constant, and Θ(x) is the Heaviside function. We use a disk radius of R = 1.0. The system density ϕ is defined by the area coverage of disks, ϕ = N πR2/L2, giving us a range of ϕ = 0.1745 to ϕ = 0.8375. We randomly place Np non-overlapping pinning sites which are modeled as parabolic traps that exert a force on the disks of the form Fp = Fp(r/Rp)Θ(r−Rp)∧r, where ∧r is the displacement vector from the pinning site center to the disk center, r=|r|, Fp is the maximum pinning force, and Rp is the pinning site radius. We set Rp=0.5 to ensure that at most one disk can be pinned by a given pinning site. We apply a uniform external drive FD=FD∧x on each disk in the x-direction and measure the resulting average drift velocity per disk in the direction of the drive 〈V 〉 = N−1 ∑Ni=0 〈vi · ∧ x 〉 to produce velocity-force curves.
The disk dynamics is obtained by integrating the following overdamped equation of motion: ηdr/dt = Finter + Fm + Fp + FD, where η = 1 is the drag coefficient. The disk self-propulsion is produced by the motor force Fm which acts on a given disk in a fixed randomly chosen direction for a run time τ that is chosen from a uniform random distribution over the range [tr,2tr]. After τ simulation time steps have elapsed, the motor force instantly reorients to a new randomly chosen direction, which it maintains for the next τ simulation time steps before reorienting again. In the absence of other disks, pinning sites, or obstacles, a disk would move a distance D during one running time, where D is uniformly randomly distributed over the range [rl, 2rl] with rl=tr Fm δt. We use Fm = 1.0 and run times ranging from tr=1000 to tr=2.4 ×106 simulation steps, with a simulation time step of δt = 0.001. To initialize the system, we place the disks in random configurations and increase FD by increments of δFD=0.25, spending 1 ×106 simulation time steps at each increment. This protocol allows us to ensure that the system has reached a steady state before we perform our measurements. An alternative protocol is to increase the driving force continuously. If the rate of increase is slow, both protocols produce the same results and the behavior of the system is not hysteretic. Rapid rates of change of the driving force can induce hysteresis and other rate-dependent phenomena similar to that observed in other systems driven over random disorder that exhibit depinning transitions [2]; however, an exploration of such effects is beyond the scope of this work. Rate-dependent effects may be particularly enhanced in active matter systems as there is a time scale associated with the run time. We allow our system to remain at each driving force increment value much longer than any of the run times we consider in order to ensure that we have reached a steady state.
Fig1.png
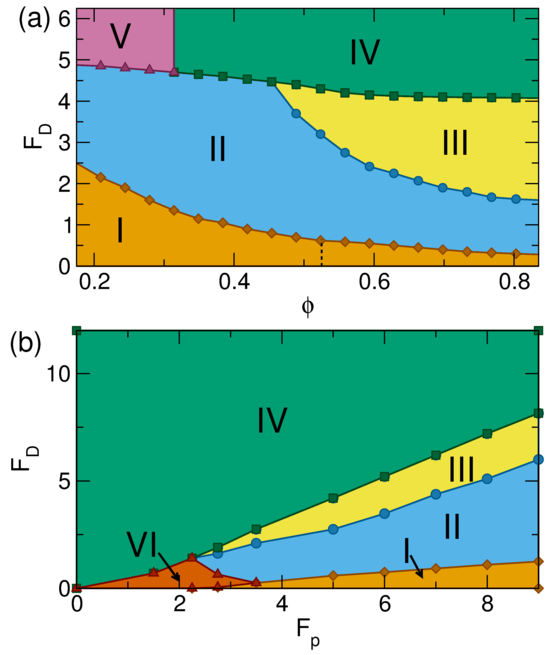
Figure 1: Images of disk locations (dots) in a system with ϕ = 0.55, rl = 300, N/Np = 2.0, and Fp = 5.0. Disks are colored according to the cluster to which they belong, with the largest cluster shown in blue, the second largest in red, the third largest in green, the fourth largest in purple, and the fifth largest in orange. All remaining clusters, including isolated disks, are colored black. White areas contain no disks. The disks are driven in the positive x direction with a driving force of FD. (a) At FD = 0.0, the system forms a uniform disordered state. (b) Disk trajectories (lines) in a portion of the sample at FD = 0.5, where the system is in a plastic flow state. (c) At FD = 3.25, a dense stripe coexists with a pinned liquid. The stripe structure is moving in the positive x direction. (d) At FD = 6.0, a fully phase separated state appears with a large cluster that translates in the positive x direction.

III.  DYNAMIC PHASES AND TRANSPORT ON PINNING SITES

A.  Changing disk density and pinning strength

In Fig. 1 we illustrate the disk locations for a system with ϕ = 0.55, rl = 300, N/Np = 2.0, and Fp = 5.0. For these values of ϕ and rl, in the absence of pinning the system forms a phase separated state in which the disks condense into a single large dense cluster. When pinning is present, Fig. 1(a) shows that at FD = 0, the system forms a homogeneous disordered phase. We identify disks that are in contact with one another using the Luding and Herrmann cluster algorithm [41], and plot the largest cluster in blue, the second largest cluster in red, and the next largest clusters in green, purple, and orange. In Fig. 1(a) for FD=0, the largest cluster percolates across the entire sample. At FD = 0.5 in Fig. 1(b), we observe a plastic flow state, as indicated by the riverlike disk trajectories, in which the overall disk density remains uniform. As FD increases, a transition occurs into a moving stripe state as shown in Fig. 1(c) for FD = 3.25. The dense stripe is oriented parallel to the driving force and moves in the positive x direction. The disks that are not in the dense phase are directly trapped by the pinning sites. As FD approaches Fp, more of the pinned disks become mobile and the system enters the fully phase separated state illustrated in Fig. 1(d) for FD = 6.0, where a single large clump appears that translates in the direction of drive but has has no particular orientation with respect to the driving direction.
Fig2.png
Figure 2: (a) The velocity 〈V〉 vs FD for the system in Fig. 1(a) with Fp = 5.0, rl=300, Np = 8000, and varied ϕ ranging from ϕ = 0.1745 to ϕ = 0.8375, corresponding to N=5000 to N=24000 in the figure legend. The letters a to d indicate the values of FD at which the images in Fig. 1 were obtained for the ϕ = 0.55 which corresponds to the 16k curve. (b) The corresponding d〈V〉/dFD vs FD curves. (c) The size of the largest cluster ~CL vs FD. The dashed line indicates the transition into the moving stripe state, and the solid line denotes the transition to the moving phase separated state. (d) The number of six-fold coordinated disks ~P6 vs FD. The error bars in this and all remaining figures are smaller than the size of the symbols.
In Fig. 2(a) we plot the velocity-force curves for the system in Fig. 1 at disk densities ranging from ϕ = 0.1745 to ϕ = 0.8375 in increments of δϕ = 0.035, while in Fig. 2(b) we show the corresponding d〈V〉/dFD curves. The letters a to d indicate the values of FD at which the images in Fig. 1 were obtained for the ϕ = 0.55 sample (which corresponds to 16,000 disks), demonstrating that the different phases correlate with distinct features in the transport curves. Previous studies of superconducting vortex systems showed that a peak in d〈V〉/dFD, the derivative of the velocity-force curve, is associated with a dynamical phase transition from plastic flow to a moving lattice state [2,3,8]. In more complex systems, such as driven pattern forming systems, multiple peaks in the d〈V〉/dFD curves coincide with multiple transitions in the structure of the moving state [42,43]. In Fig. 2(a), a depinning transition occurs at a critical driving force Fc which shifts to lower values as ϕ increases. The d〈V〉/dFD curves in Fig. 2(b) have a double peak feature, with the largest peak near near FD = 4.0 and a smaller peak at lower values of FD. Both peak features become less distinct as ϕ increases. The transition from a pinned state to plastic flow occurs at the point at which d〈V〉/dFD first rises above zero, while the moving stripe phase appears just above the first peak in d〈V〉/dFD. The second peak in d〈V〉/dFD is associated with a transition to a moving fully phase separated state or to a uniformly dense state in which all the disks are in motion.
In Fig. 2(c,d) we plot the size of the largest cluster ~CL and the number of six-fold coordinated disks ~P6, obtained from a Voronoi tessellation, versus FD for the system in Fig. 2(a,b). For clarity, both ~CL and ~P6 are plotted in terms of the total number of disks and are not normalized to range between 0 and 1. For ϕ < 0.314, the system is in the moving disordered state for all values of FD. For FD = 0, there is a pinned labyrinth phase similar to that shown in Fig. 1(a) for ϕ > 0.525, while for ϕ < 0.525 there is a pinned liquid state similar to that illustrated in Fig. 3(c) at ϕ = 0.35. At low drives, a drop in ~CL occurs when the labyrinth phase breaks apart into a moving disordered phase, as illustrated in Fig. 1(b). The dashed line highlights an increase in ~CL that occurs when the system enters a moving stripe phase. In Fig. 2(c) the thick solid line highlights an increase in ~CL that occurs near FD = 4.0, which is also the location of the largest peak in d〈V〉/dFD. In Fig. 2(d), there is an upward jump in ~P6 near FD = 4.0, marked with a solid line, at the transition into the moving fully phase separated state. At lower FD there is a smaller jump in ~P6 marked with a dashed line connected with the transition into a moving stripe state. There is an increase in ~P6 whenever dense regions of disks form since the densely packed regions have triangular ordering with disks that are mostly sixfold coordinated. We note that in the labyrinth phase, ~CL can be large since a cluster can percolate across the entire system as illustrated in Fig. 1(a), but ~P6 remains low since the disks within the labyrinth are disordered.
Fig3.png
Figure 3: Image of disk locations (dots) in a sample with rl = 300, Np = 8000, and Fp = 5.0. Disks are colored according to the cluster to which they belong, with the largest cluster shown in blue. White regions contain no disks. (a) The uniform disordered state for ϕ = 0.8375 and FD = 0. (b) The moving stripe state for ϕ = 0.8375 and FD = 1.5. The stripe structure moves in the positive x direction. (c) The pinned liquid state for ϕ = 0.35 and FD = 0. (d) The moving phase separated state for ϕ = 0.35 and FD=5.0, where all disks move in the positive x direction.
In Fig. 3(a) we illustrate the pinned cluster state at FD = 0 and ϕ = 0.8375, while Fig. 3(b) shows the moving stripe state at the same disk density for FD = 1.5. The stripe structure moves in the positive x direction, parallel to the drive. Figure 3(c) shows the pinned liquid phase at FD = 0 and ϕ = 0.35, where the clusters are absent, and Fig. 3(d) illustrates the moving phase separated state at ϕ = 0.35 and FD = 5.0.
Fig4.png
Figure 4: (a) The dynamic phase diagram as a function of FD vs ϕ constructed from the features in Fig. 2 for a sample with Fp = 5.0, Np = 8000, and rl = 300. I: pinned phase; II: plastic flow phase; III: moving stripe phase; IV: moving fully phase separated state; V: moving liquid phase. The dashed line in phase I indicates the separation between a pinned liquid and a pinned labyrinth state. (b) The dynamic phase diagram as a function of FD vs Fp for a sample with ϕ = 0.55, N/Np = 2.0, and rl = 300. The phases I through V are marked as above. Phase VI is the moving phase separated state in which some disks can be temporarily pinned.
From the features in ~CL, ~P6, and the transport curves in Fig. 2, we identify distinct dynamic phases as plotted in Fig. 4. As a function of FD versus ϕ, shown in Fig. 4(a), we find five dynamic phases, marked I through V. There is a transition out of phase I, the pinned phase, at the depinning threshold Fc, which drops to lower FD with increasing ϕ. A dashed line marks the transition between ϕ < 0.525, where the pinned clusters do not percolate and a pinned liquid of the type shown in Fig. 3(c) forms, and ϕ > 0.525, where a pinned percolating cluster appears as illustrated in Fig. 1(a) and Fig. 3(a). In phase II, plastic flow of the type illustrated in Fig. 1(b) occurs, and the disk density is mostly homogeneous. Phase III, the moving stripe phase, is shown in Fig. 1(c) and Fig. 3(b). Figures 1(d) and 3(d) illustrate phase IV, the moving fully phase separated state, while in phase V, the moving liquid state, no clustering occurs but all the disks are moving.
Fig5.png
Figure 5: (a) d〈V〉/dFD vs FD in samples with ϕ = 0.55, N/Np = 2.0, and rl = 300 from the system in Fig. 4(b) for different values of Fp ranging from Fp=0 to Fp=9.0. As Fp increases, a second peak appears and shifts to higher FD. (b) The corresponding P6 vs FD.
We have also examined the dynamic phases as a function of the pinning strength Fp. In Fig. 5(a) we plot d〈V〉/dFD versus FD for a system with ϕ = 0.55 and N/Np = 2.0 over the range Fp = 0 to Fp=9.0. A double peak in d〈V〉/dFD occurs only when Fp > 1.5, and both peaks shift to higher values of FD with increasing Fp. Figure 5(b) shows the corresponding normalized fraction of sixfold coordinated disks P6=~P6/N versus FD. For Fp > 3.5, the disks are disordered and P6 ≈ 0.5. When the system enters phase III, a feature appears near P6 = 0.75, and there is a jump up in P6 at the onset of phase IV. For low pinning strengths of Fp < 2.75, a moving phase separated state called phase VI appears in which some disks can be temporarily pinned, while for large enough FD all the disks are moving and the system enters phase IV, the flowing state. The dynamic phase diagram as a function of FD versus Fp in Figure 4(b) indicates that phase III flow only occurs for Fp > 2.0, while phases I and III grow in extent with increasing Fp. In Fig. 4(b) at FD = 0.0 there is a transition from phase VI, the pinned phase separated state, to the disordered pinned phase I for Fp > 2.0. It may be possible to analyze several of these phases in terms of driven diffusion or driven Ising lattice models by mapping the activity into the model.
The general features of the FD versus Fp dynamic phase diagram in Fig. 4 exhibit several similarities to the FD versus Fp dynamic phase diagram found for vortices in type-II superconductors [1,2]. In the vortex system, there is an analogous transition from a pinned phase to a plastic flow phase which shifts to higher FD with increasing Fp. There is also a transition from the plastic flow phase to a moving ordered phase in which all of the vortices are moving, which is analogous to the II-IV transition we observe. There is no equivalent to our phase III in the vortex system since a moving vortex crystal cannot coexist with pinned vortices.
Fig6.png
Figure 6: (a) d〈V〉/dFD vs FD for samples with ϕ = 0.55, Fp = 5.0, and N/Np = 2.0 for varied rl ranging from rl=1 to rl=1200. The magnitude of the second peak in d〈V〉/dFD decreases with decreasing rl. (b) The corresponding 〈V〉 vs FD curves. (c) The corresponding P6 vs FD curves, indicating that phase IV disappears for rl < 60.
Fig7.png
Figure 7: (a) The dynamic phase diagram as a function of FD vs rl constructed from the features in Fig. 6 for a sample with ϕ = 0.55, Np = 8000, and Fp = 5.0. I: pinned phase; II: plastic flow phase; III: moving stripe phase; IV: moving fully phase separated state; V: moving liquid phase. (b) The dynamic phase diagram as a function of FD vs the number of pinning sites Np in samples with ϕ = 0.55, Fp = 5.0, and rl = 300.

B.  Changing run length and pinning density

In Fig. 6(b) we plot the velocity-force curves and in Fig. 6(a) we show the corresponding d〈V〉/dFD curves for a system with Fp = 5.0, ϕ = 0.55, and N/Np = 2 for varied run lengths from rl=1.0 to rl=1200. The curves follow each other closely except for the second peak in d〈V〉/dFD, which increases in magnitude with increasing rl. The second peak is absent at lower rl when a transition from phase II to phase V occurs, but materializes at larger rl once a transition from phase III to phase IV begins to occur. In Fig. 6(c) we plot the corresponding P6 versus FD curves which show the onset of the transition into region IV in the form of an increase in P6. In Fig. 7(a), we show the dynamic phase diagram as a function of FD versus rl for the system in Fig. 6, where phases IV and III only occur for rl > 60. For rl < 60, phase IV, the moving phase separated state, disappears, and the system passes directly from phase II plastic flow to the phase V moving liquid. Here, the line marking the phase II to phase V transition remains flat at FD=Fp=5.0. These results indicate that the generic phases we observe are robust for rl values both larger and smaller than the system size L. We have performed simulations on samples of smaller size and find the same features in the phase diagram, since a key parameter is the strength of the pinning relative to the driving force, which is independent of sample size.
We have also examined the case of fixed ϕ = 0.55 and rl = 300 to obtain the dynamic phase diagram as a function of FD versus Np, shown in Fig. 7(b). Phase III diminishes in width until Np/N = 1.0. For larger Np, there is a direct transition from phase II to phase IV, and phase III flow disappears. Our results indicate that the dynamic phases we observe persist over a wide range of parameters and represent generic features of this class of system.

IV.  DYNAMICS IN OBSTACLE ARRAYS

Fig8.png
Figure 8: (a) 〈V〉 vs FD for systems with ϕ = 0.55 and rl = 300 for varied numbers of obstacles No=2000 to No=12000. The inset shows the normalized cluster size CL vs the number of obstacles No for ϕ = 0.55 and rl = 300 at FD = 0.0, where there is a transition from a phase separated state at low FD to a uniform state at high FD. (b) d〈V〉/dFD vs FD, corresponding to the system in panel (a), lacks any peak features. (c) The corresponding normalized P6 vs FD has a smooth monotonic behavior.
Fig9.png
Figure 9: Images of disk locations (dots) in samples with ϕ = 0.55 and rl = 300 containing obstacles consisting of fixed disks (not shown). (a) At FD = 0 and No=8000 obstacles, a disordered state appears. (b) At FD = 6.0 and No=8000, the system is still disordered. (c) FD = 0 and No=2000. (d) At FD=2.0 and No=2000, a moving stripe state forms.
Active disks moving through obstacle arrays have a very different behavior than that described in Section III for active disks in pinning arrays. To explore this, we prepare an obstacle landscape in which the obstacles are modeled as immobile disks with a radius of 1.0. We consider a system with rl=300, a mobile disk density of ϕ = 0.55, and No obstacles. An obstacle-free system at this disk density and running length rl forms a phase separated state for FD = 0. As we increase the number of obstacles No, we find a transition from a phase separated state to a uniform liquid state, as indicated in the plot of the normalized value of CL versus No in the inset of Fig. 8(a). We show snapshots of the disk and obstacle positions in Fig. 9. At FD=0, Fig. 9(a) indicates that a sample containing No=8000 obstacles is disordered, while Fig. 9(c) shows that when No=2000 obstacles are present, the system is density phase separated. In Fig. 8 we plot the velocity 〈V〉, d〈V〉/dFD, and P6 versus FD for varied numbers of obstacles No. As No increases, the average value of 〈V〉 monotonically deceases, and the d〈V〉/dFD curve contains no peaks, unlike the behavior for a pinning substrate. There is a gradual decrease in P6 with increasing FD, and there are no peaks or dips in P6 of the type that appear for the pinning substrate. In general, we find that the obstacles produce no clear changes in the structure of the moving phase. When the number of obstacles No > 7000, the system undergoes plastic depinning into river-like channel flow, and remains in a uniform density, disordered flow state up to the highest drives FD that we considered, as shown in Fig. 9(b) for a sample with No=8000 at FD = 6.0. Conversely, for No < 7000, the system remains in a phase separated state, and forms a moving stripe structure resembling that illustrated in Fig. 9(d) for No=2000 at FD = 2.0. This result indicates that there are no dynamical transitions in the moving state for self-propelled disks moving through obstacle arrays; however, there is a transition in the drive-free limit of FD = 0 as a function of obstacle density.
In a recent experimental paper, Morin et al. [44] examine a colloidal flocking active matter system drifting through an obstacle array and find that when there are a large number of obstacles, the flocking behavior is lost and the flow develops riverlike properties similar to that observed in other depinning systems and resembling what we find in Fig. 1(b). In addition, Morin et al. report that there is a critical obstacle density above which the flocking behavior disappears, not unlike the cluster disappearance at high obstacle densities that we observe in Fig. 9(a). Beyond obstacle arrays, it is also possible to have active matter move over landscapes of pinning sites created via optical means, as has been demonstrated in other recent experiments [45,46].

V.  SUMMARY

We have shown that active matter assemblies driven over random pinning arrays represent a new class of system that exhibit pinning, depinning, and nonequilibrium phase transitions similar to those found for driven vortices and colloids moving over random disorder. In a regime where the system forms a phase separated state in the absence of pinning, we find that the addition of pinning causes the formation of a disordered uniform state that depins plastically into a flowing uniform state with riverlike features. At higher drives, this is followed by a transition to a moving dense stripe phase coexisting with a pinned liquid, until at the highest drives, the system transitions into a moving fully phase separated state. The different transitions are associated with features in the velocity-force and d〈V〉/dFD curves that are similar to the features observed in driven non-active systems with quenched disorder. In contrast, for substrates composed of obstacle arrays, there are no dynamical transitions in the moving state and correspondingly there is a lack of features in the transport curves. At zero drive, there is a transition from a phase separated state to a disordered state as the obstacle density increases.

ACKNOWLEDGMENTS

This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396. Cs. Sándor and A. Libál thank the Nvidia Corporation for their graphical card donation that was used in carrying out these simulations.

References

[1]
D. S. Fisher, Collective transport in random media: from superconductors to earthquakes, Phys. Rep. 301, 113 (1998).
[2]
C. Reichhardt and C.J. Olson Reichhardt, Depinning and nonequilibrium dynamic phases of particle assemblies driven over random and ordered substrates: a review, Rep. Prog. Phys. 80, 026501 (2017).
[3]
S. Bhattacharya and M. J. Higgins, Dynamics of a disordered flux line lattice, Phys. Rev. Lett. 70, 2617 (1993).
[4]
A.E. Koshelev and V.M. Vinokur, Dynamic melting of the vortex lattice, Phys. Rev. Lett. 73, 3580 (1994).
[5]
A.C. Marley, M.J. Higgins, and S. Bhattacharya, Flux flow noise and dynamical transitions in a flux line lattice, Phys. Rev. Lett. 74, 3029 (1995).
[6]
L. Balents, M.C. Marchetti, and L. Radzihovsky, Nonequilibrium steady states of driven periodic media, Phys. Rev. B 57, 7705 (1998).
[7]
P. Le Doussal and T. Giamarchi, Moving glass theory of driven lattices with disorder, Phys. Rev. B 57, 11356 (1998).
[8]
C.J. Olson, C. Reichhardt, and F. Nori, Nonequilibrium dynamic phase diagram for vortex lattices, Phys. Rev. Lett. 81, 3757 (1998).
[9]
F. Pardo, F. de la Cruz, P. L. Gammel, E. Bucher, and D.J. Bishop, Observation of smectic and moving-Bragg-glass phases in flowing vortex lattices, Nature (London) 396, 348 (1998).
[10]
G. Grüner, The dynamics of charge-density waves, Rev. Mod. Phys. 60, 1129 (1988).
[11]
F.I.B. Williams, P.A. Wright, R.G. Clark, E.Y. Andrei, G. Deville, D.C. Glattli, O. Probst, B. Etienne, C. Dorin, C.T. Foxon, and J.J. Harris, Conduction threshold and pinning frequency of magnetically induced Wigner solid, Phys. Rev. Lett. 66, 3285 (1991).
[12]
C. Zhang, R.-R. Du, M.J. Manfra, L.N. Pfeiffer, and K.W. West, Transport of a sliding Wigner crystal in the four flux composite fermion regime, Phys. Rev. B 92, 075434 (2015).
[13]
J. Iwasaki, M. Mochizuki, and N. Nagaosa, Universal current-velocity relation of skyrmion motion in chiral magnets, Nature Commun. 4, 1463 (2013).
[14]
C. Reichhardt, D. Ray, and C.J. Olson Reichhardt, Collective transport properties of driven skyrmions with random disorder, Phys. Rev. Lett. 114, 217202 (2015).
[15]
X. Wang, H. Fu, L. Du, X. Liu, P. Wang, L.N. Pfeiffer, K.W. West, R.-R. Du, and X. Lin, Depinning transition of bubble phases in a high Landau level, Phys. Rev. B 91, 115301 (2015).
[16]
A. Vanossi, N. Manini, M. Urbakh, S. Zapperi, and E. Tosatti, Modeling friction: From nanoscale to mesoscale, Rev. Mod. Phys. 85, 529 (2013).
[17]
B. Bakó, D. Weygand, M. Samaras, W. Hoffelner, and M. Zaiser, Dislocation depinning transition in a dispersion-strengthened steel, Phys. Rev. B 78, 144104 (2008).
[18]
I. Regev, J. Weber, C. Reichhardt, K.A. Dahmen, and T. Lookman, Reversibility and criticality in amorphous solids, Nature Commun. 6, 8805 (2015).
[19]
B. Tyukodi, S. Patinet, S. Roux, and D. Vandembroucq, From depinning transition to plastic yielding of amorphous media: A soft-modes perspective, Phys. Rev. E 93, 063005 (2016).
[20]
J.M. Carlson, J.S. Langer, and B.E. Shaw, Dynamics of earthquake faults, Rev. Mod. Phys. 66, 657 (1994).
[21]
M. Paczuski and S. Boettcher, Universality in sandpiles, interface depinning, and earthquake models, Phys. Rev. Lett. 77, 111 (1996).
[22]
E. Rolley, C. Guthmann, R. Gombrowicz, and V. Repain, Roughness of the contact line on a disordered substrate, Phys. Rev. Lett. 80, 2865 (1998).
[23]
W. Xu and C.-H. Choi, From sticky to slippery droplets: Dynamics of contact line depinning on superhydrophobic surfaces, Phys. Rev. Lett. 109, 024504 (2012).
[24]
C. Reichhardt and C.J. Olson, Colloidal dynamics on disordered substrates, Phys. Rev. Lett. 89, 078301 (2002).
[25]
A. Pertsinidis and X.S. Ling, Statics and dynamics of 2D colloidal crystals in a random pinning potential, Phys. Rev. Lett. 100, 028303 (2008).
[26]
P. Tierno, Depinning and collective dynamics of magnetically driven colloidal monolayers, Phys. Rev. Lett. 109, 198304 (2012).
[27]
T. Bohlein, J. Mikhael, and C. Bechinger, Observation of kinks and antikinks in colloidal monolayers driven across ordered surfaces, Nature Mater. 11, 126 (2012).
[28]
M.P.N. Juniper, A.V. Straube, R. Besseling, D.G.A.L. Aarts, and R.P.A. Dullens, Microscopic dynamics of synchronization in driven colloids, Nature Commun. 6, 7187 (2015).
[29]
M.C. Marchetti, J.F. Joanny, S. Ramaswamy, T.B. Liverpool, J. Prost, M. Rao, and R.A. Simha, Hydrodynamics of soft active matter, Rev. Mod. Phys. 85, 1143 (2013).
[30]
C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe, and G. Volpe, Active Brownian particles in complex and crowded environments, Rev. Mod. Phys. 88, 045006 (2016).
[31]
Y. Fily and M.C. Marchetti, Athermal phase separation of self-propelled particles with no alignment, Phys. Rev. Lett. 108, 235702 (2012).
[32]
G.S. Redner, M.F. Hagan, and A. Baskaran, Structure and dynamics of a phase-separating active colloidal fluid, Phys. Rev. Lett. 110, 055701 (2013).
[33]
J. Palacci, S. Sacanna, A.P. Steinberg, D.J. Pine, and P.M. Chaikin, Living crystals of light-activated colloidal surfers, Science 339, 936 (2013).
[34]
I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, and C. Bechinger, Dynamical clustering and phase separation in suspensions of self-propelled colloidal particles, Phys. Rev. Lett. 110, 238301 (2013).
[35]
M.E. Cates and J. Tailleur, Motility-induced phase separation, Ann. Rev. Condens. Mat. Phys. 6, 219 (2015).
[36]
M.E. Cates and J. Tailleur, When are active Brownian particles and run-and-tumble particles equivalent? Consequences for motility-induced phase separation, Europhys. Lett. 101, 20010 (2013).
[37]
C. Reichhardt and C.J.O. Reichhardt, Active microrheology in active matter systems: Mobility, intermittency, and avalanches, Phys. Rev. E 91, 032313 (2015).
[38]
C. Reichhardt and C.J.O. Reichhardt, Active matter transport and jamming on disordered landscapes, Phys. Rev. E 90, 012701 (2014).
[39]
O. Chepizhko, E.G. Altmann, and F. Peruani, Optimal noise maximizes collective motion in heterogeneous media, Phys. Rev. Lett. 110, 238101 (2013).
[40]
D. Quint and A. Gopinathan, Topologically induced swarming phase transition on a 2D percolated lattice, Phys. Biol. 17, 046008 (2015).
[41]
S. Luding and H.J. Herrmann, Cluster-growth in freely cooling granular media, Chaos 9, 673 (1999).
[42]
C. Reichhardt, C.J.O. Reichhardt, I. Martin, and A.R. Bishop, Dynamical ordering of driven stripe phases in quenched disorder, Phys. Rev. Lett. 90, 026401 (2003).
[43]
H.J. Zhao, V.R. Misko, and F.M. Peeters, Dynamics of self-organized driven particles with competing range interaction, Phys. Rev. E 88, 022914 (2013).
[44]
A. Morin, N. Desreumaux, J.-B. Caussin, and D. Bartolo, Distortion and destruction of colloidal flocks in disordered environments, Nature Phys. 13, 63 (2017).
[45]
E. Pince, S.K.P. Velu, A. Callegari, P. Elahi, S. Gigan, G. Volpe, and G. Volpe, Disorder-mediated crowd control in an active matter system, Nature Commun. 7, 10907 (2016).
[46]
C. Lozano, B. ten Hagen, H. Löwen, and C. Bechinger, Phototaxis of synthetic microswimmers in optical landscapes, Nature Commun. 7, 12828 (2016).


File translated from TEX by TTHgold, version 4.00.
 Back to Home