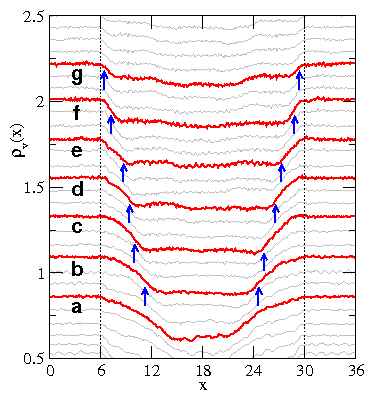
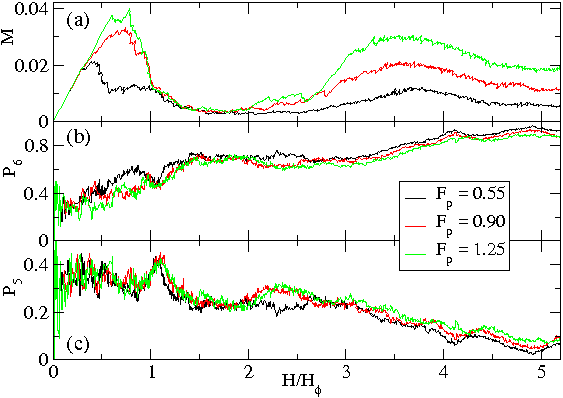
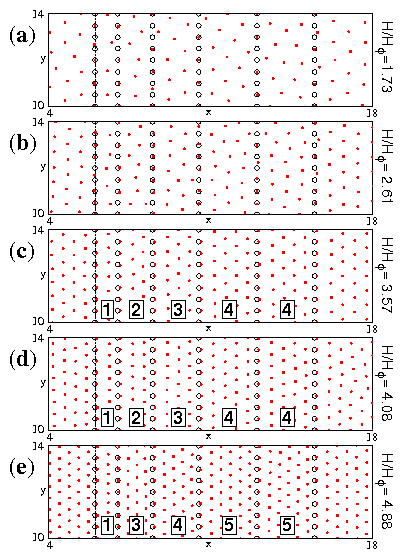
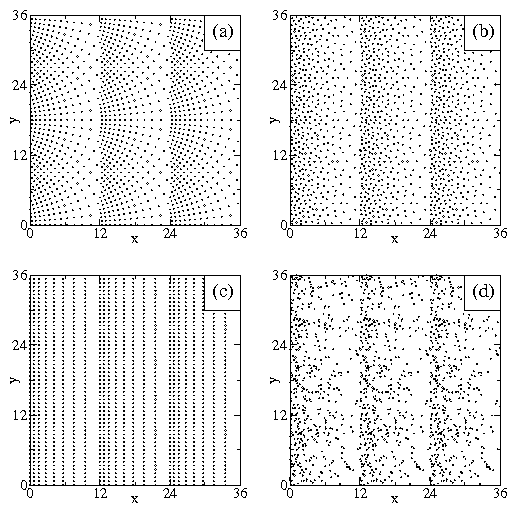
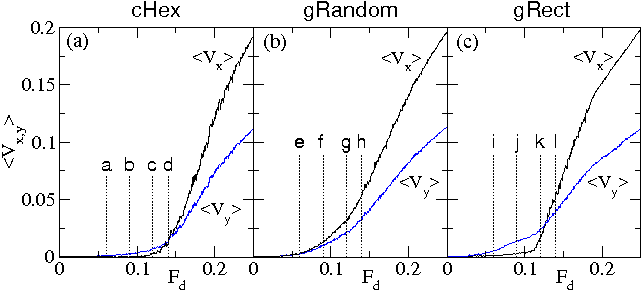
 Figure 16:
The average vortex velocity in the x-direction 〈Vx 〉
vs Fd for current-driven simulations of
cHex, cSquare, cPenrose, gRect, gRandom, and uRandom transport arrays
with Fp = 0.55 and a drive angle of θ = 0
at different vortex densities.
(a) H/Hϕ = 1.4 for cHex, cSquare, cPenrose, uRandom, gRandom,
and gRect,
from lower right to upper right.
(b) H/Hϕ = 0.8 for cSquare, cHex, cPenrose, uRandom, gRandom,
and gRect,
from lower right to upper right.
(c) H/Hϕ = 2.2 for gRect,
cHex, cSquare, cPenrose, uRandom, and gRandom,
from lower right to upper right.
In general, the conformal arrays have a higher depinning threshold and lower
vortex velocity than the non-conformal arrays.
The gRect array exhibits a large depinning threshold at
H/Hϕ = 2.2 due to a commensuration effect.
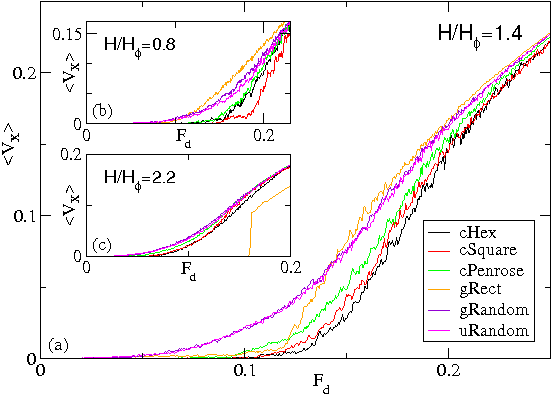
Figure 16:
The average vortex velocity in the x-direction 〈Vx 〉
vs Fd for current-driven simulations of
cHex, cSquare, cPenrose, gRect, gRandom, and uRandom transport arrays
with Fp = 0.55 and a drive angle of θ = 0
at different vortex densities.
(a) H/Hϕ = 1.4 for cHex, cSquare, cPenrose, uRandom, gRandom,
and gRect,
from lower right to upper right.
(b) H/Hϕ = 0.8 for cSquare, cHex, cPenrose, uRandom, gRandom,
and gRect,
from lower right to upper right.
(c) H/Hϕ = 2.2 for gRect,
cHex, cSquare, cPenrose, uRandom, and gRandom,
from lower right to upper right.
In general, the conformal arrays have a higher depinning threshold and lower
vortex velocity than the non-conformal arrays.
The gRect array exhibits a large depinning threshold at
H/Hϕ = 2.2 due to a commensuration effect.
|