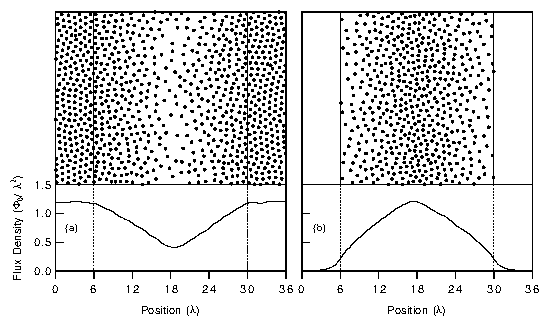
 Figure 1: Top view of the region where flux lines, indicated by dots, move.
(a) Snapshot during the initial ramp-up phase,
(b) snapshot of the remnant magnetization after ramping down the external
field. The bottom panels show
B(x) = (36 λ)−1 ∫036λ dy B(x,y),
i.e., the flux density profile versus x, averaged over the vertical
direction y.
The 24 λ×36 λ sample has 3456 pinning sites, and
fp=0.9f0.
Figure 1: Top view of the region where flux lines, indicated by dots, move.
(a) Snapshot during the initial ramp-up phase,
(b) snapshot of the remnant magnetization after ramping down the external
field. The bottom panels show
B(x) = (36 λ)−1 ∫036λ dy B(x,y),
i.e., the flux density profile versus x, averaged over the vertical
direction y.
The 24 λ×36 λ sample has 3456 pinning sites, and
fp=0.9f0.
|

