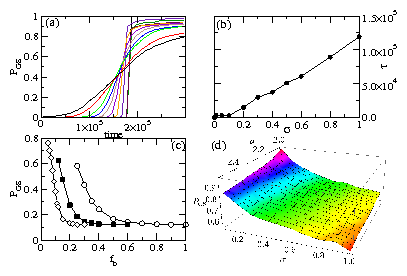
 Figure 4: (a) Percentage PGS of ice-rule obeying ground state vertices
vs time during the dynamical annealing process for different
disorder widths σ. From upper right to lower right,
σ = 0, 0.01, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.8,
and 1.0. Here, a=2.5λ, l=5/6λ, and fb=0.25.
(b) Relaxation time τ vs σ for the
same system.
(c)
Final value of PGS vs fb in samples
subjected to a small shaking field
with no dynamical annealing.
Here l=5/6λ, σ = 0.1,
and a=2.0λ (open circles), 2.5λ (filled squares),
and 3.0λ (open diamonds).
(d) PGS
vs
σ and a in a sample with
fb=1.0 and l=2/3λ.
Figure 4: (a) Percentage PGS of ice-rule obeying ground state vertices
vs time during the dynamical annealing process for different
disorder widths σ. From upper right to lower right,
σ = 0, 0.01, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.8,
and 1.0. Here, a=2.5λ, l=5/6λ, and fb=0.25.
(b) Relaxation time τ vs σ for the
same system.
(c)
Final value of PGS vs fb in samples
subjected to a small shaking field
with no dynamical annealing.
Here l=5/6λ, σ = 0.1,
and a=2.0λ (open circles), 2.5λ (filled squares),
and 3.0λ (open diamonds).
(d) PGS
vs
σ and a in a sample with
fb=1.0 and l=2/3λ.
|