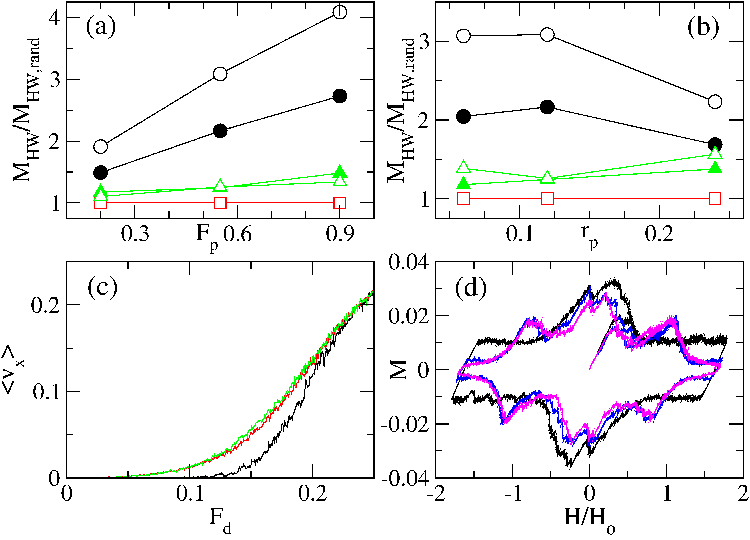
 Figure 4:
(a-b) MHW, the half-width of the magnetization loop, measured
at H/Hϕ=1.0 (filled symbols) and at H/Hϕ=1.4 (open symbols),
and normalized to
MHW for the random pinning array (red squares).
Black circles:
CPA; green triangles: random array with CPA-equivalent
pinning gradient. (a)
MHW vs Fp
for fixed
rp=0.12; (b)
MHW vs rp
for fixed Fp=0.55.
(c)
〈Vx〉 vs Fd
for vortices
driven across
a CPA (black), random array (red), and random array with
pinning gradient (green).
(d) Magnetization loops for the CPA (black) compared to periodic
pinning arrays, square (blue) and triangular (purple), at
Fp=0.55 and rp=0.12.
Figure 4:
(a-b) MHW, the half-width of the magnetization loop, measured
at H/Hϕ=1.0 (filled symbols) and at H/Hϕ=1.4 (open symbols),
and normalized to
MHW for the random pinning array (red squares).
Black circles:
CPA; green triangles: random array with CPA-equivalent
pinning gradient. (a)
MHW vs Fp
for fixed
rp=0.12; (b)
MHW vs rp
for fixed Fp=0.55.
(c)
〈Vx〉 vs Fd
for vortices
driven across
a CPA (black), random array (red), and random array with
pinning gradient (green).
(d) Magnetization loops for the CPA (black) compared to periodic
pinning arrays, square (blue) and triangular (purple), at
Fp=0.55 and rp=0.12.
|