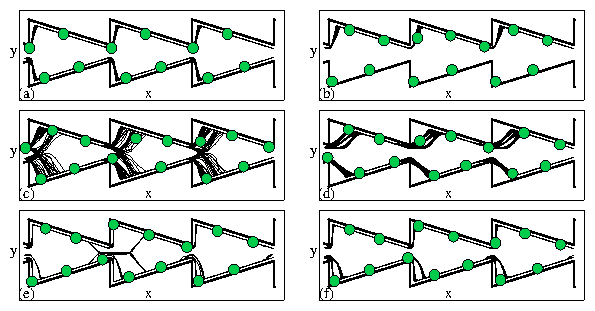
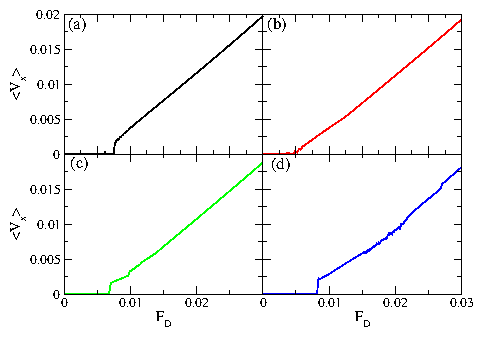
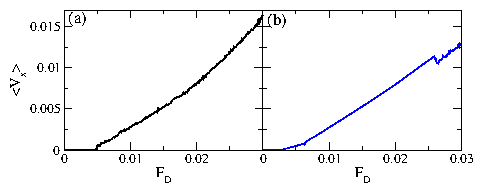
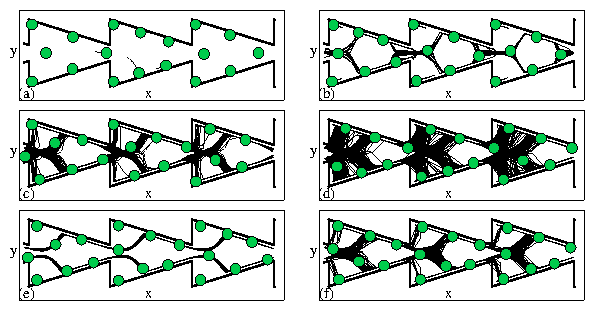
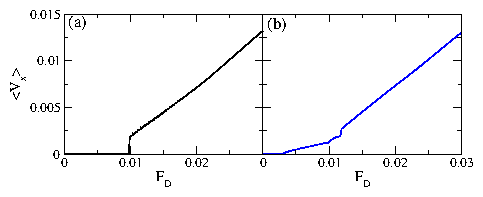
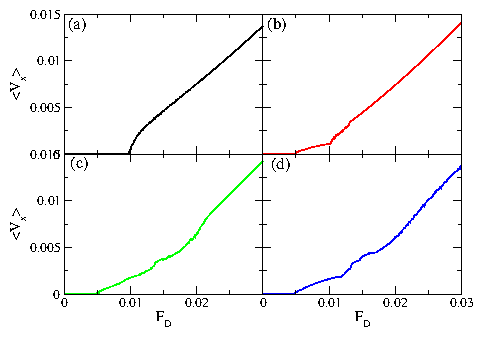
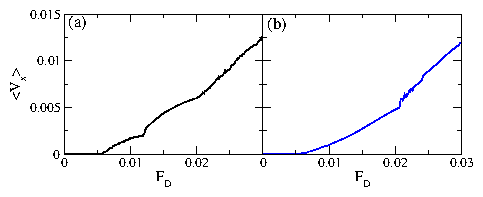
 Figure 1:
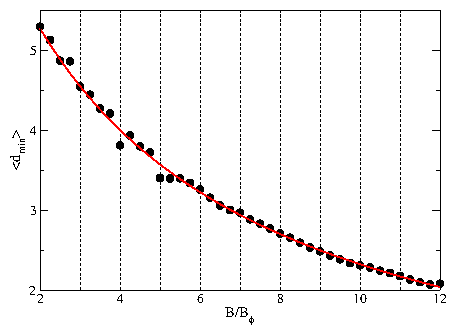
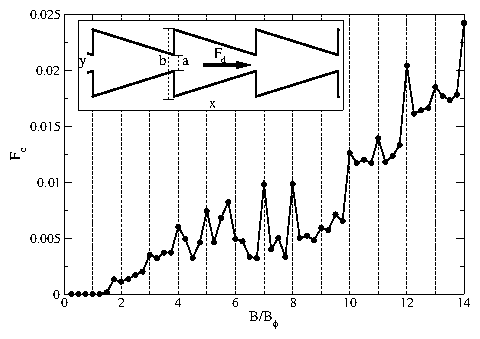
The depinning force Fc vs
B/Bϕ for vortices in a periodic funnel array for driving in
the +x, easy-flow direction.
A series of peaks
appear at matching fields of
B/Bϕ = 4, 5, 7, 8, 11, 12 and 14. Weaker peaks
occur at B/Bϕ = 3, 10, and 13,
while peaks are absent at B/Bϕ = 2, 6, and 9.
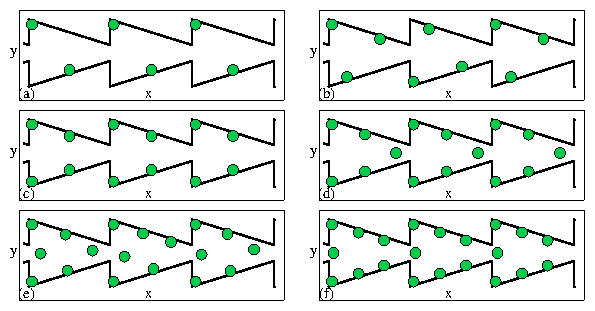
Inset: A portion of the sample showing the funnel array geometry.
Figure 1:
The depinning force Fc vs
B/Bϕ for vortices in a periodic funnel array for driving in
the +x, easy-flow direction.
A series of peaks
appear at matching fields of
B/Bϕ = 4, 5, 7, 8, 11, 12 and 14. Weaker peaks
occur at B/Bϕ = 3, 10, and 13,
while peaks are absent at B/Bϕ = 2, 6, and 9.
Inset: A portion of the sample showing the funnel array geometry.
|