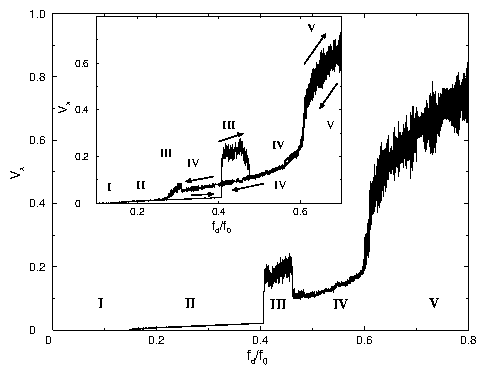
 Figure 3:
Dynamic phase diagrams with a square pinning lattice. Here,
B/Bϕ = 1.062, Bϕ = 0.25Φ0/λ2,
rp = 0.3λ, and fp = 0.625f0, unless otherwise
noted.
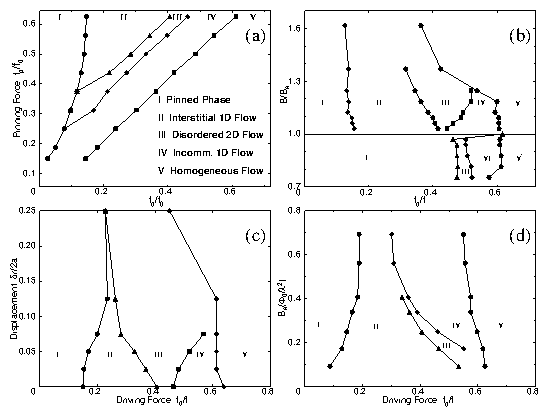
(a) Pinning force fp versus driving force fd. As
fd is increased, the phase boundaries II-III, III-IV,
and IV-V become linear.
(b) B/Bϕ versus fd. For B/Bϕ > 1, regions
I through V can be observed, with the disordered region III
growing and the ordered-flow regions II and IV reducing in
size. A similar situation occurs in (c) for gradually
increasing the amount of disorder in the location of the pins.
(d) Dynamic phase diagram for Bϕ versus fd.
Figure 3:
Dynamic phase diagrams with a square pinning lattice. Here,
B/Bϕ = 1.062, Bϕ = 0.25Φ0/λ2,
rp = 0.3λ, and fp = 0.625f0, unless otherwise
noted.
(a) Pinning force fp versus driving force fd. As
fd is increased, the phase boundaries II-III, III-IV,
and IV-V become linear.
(b) B/Bϕ versus fd. For B/Bϕ > 1, regions
I through V can be observed, with the disordered region III
growing and the ordered-flow regions II and IV reducing in
size. A similar situation occurs in (c) for gradually
increasing the amount of disorder in the location of the pins.
(d) Dynamic phase diagram for Bϕ versus fd.
|