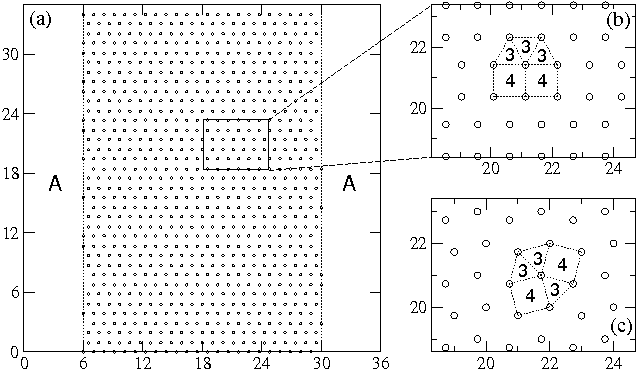
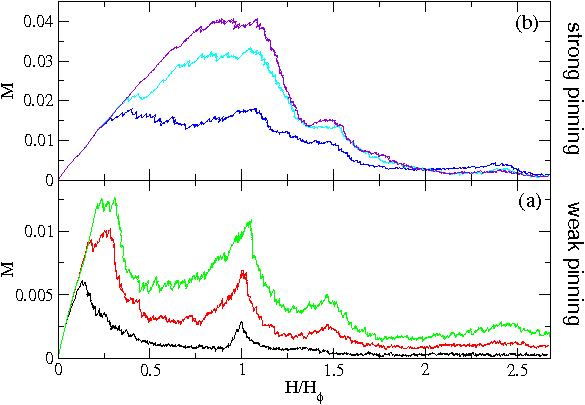
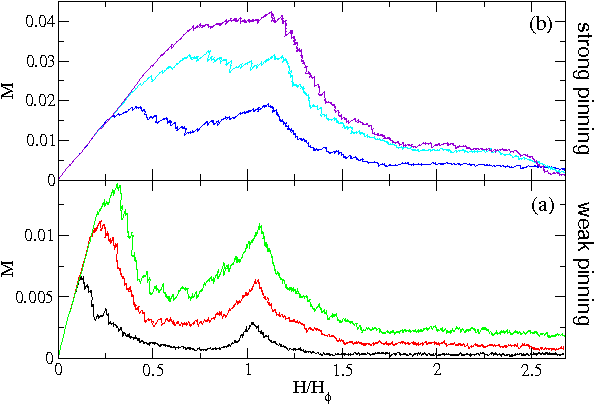
 Figure 6:
P, the fraction of occupied pins, vs H/Hϕ.
(a) The
3342
array
at Fp = 0.2, 0.3, 0.5, and 0.8, from bottom right to top right.
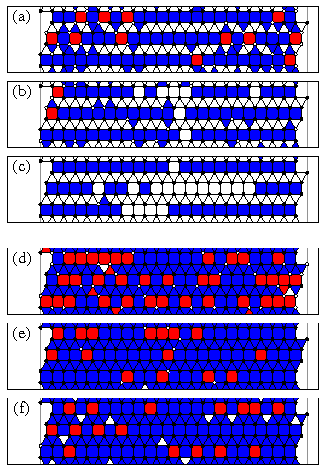
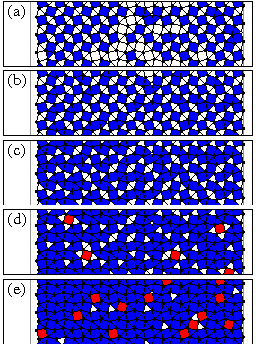
Arrows pointing to various locations on the Fp=0.3 curve
indicate field levels where we show the corresponding real-space
vortex configurations in figure 7.
(b) The
32434
array at
Fp=0.2, 0.3, 0.5, and 0.8, from bottom right to top right.
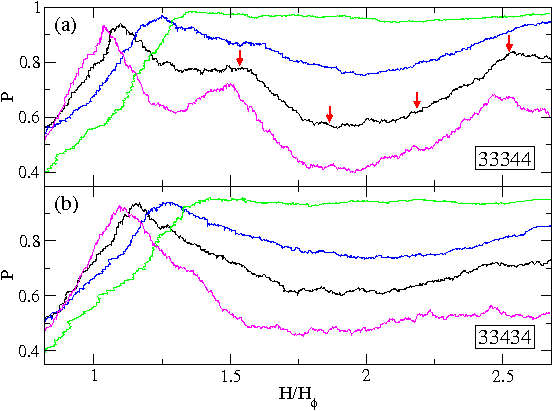
Figure 6:
P, the fraction of occupied pins, vs H/Hϕ.
(a) The
3342
array
at Fp = 0.2, 0.3, 0.5, and 0.8, from bottom right to top right.
Arrows pointing to various locations on the Fp=0.3 curve
indicate field levels where we show the corresponding real-space
vortex configurations in figure 7.
(b) The
32434
array at
Fp=0.2, 0.3, 0.5, and 0.8, from bottom right to top right.
|