Figure 4:
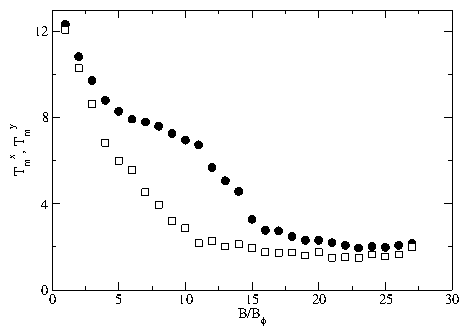
(a) The critical depinning force for two different driving directions
at matching fields B/Bϕ=1 to 27.
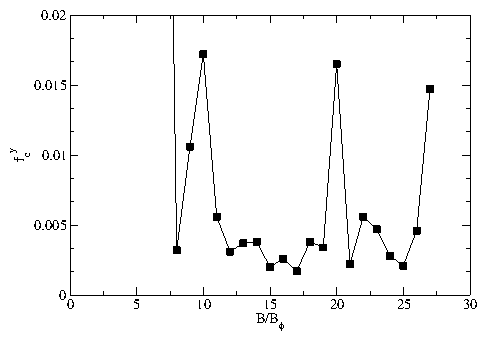
Circles: fcx for driving in the x direction; squares: fcy
for driving in the y direction.
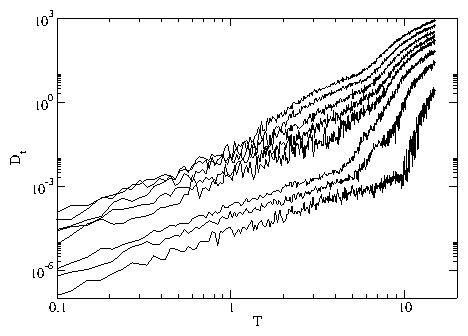
(b) Representative velocity-force curves for x-direction driving, Vx
versus fdx, for B/Bϕ= (from right to left) 1, 9, 11, 14,
17, 20, 22, 24, and 27.
Figure 4:
(a) The critical depinning force for two different driving directions
at matching fields B/Bϕ=1 to 27.
Circles: fcx for driving in the x direction; squares: fcy
for driving in the y direction.
(b) Representative velocity-force curves for x-direction driving, Vx
versus fdx, for B/Bϕ= (from right to left) 1, 9, 11, 14,
17, 20, 22, 24, and 27.
|