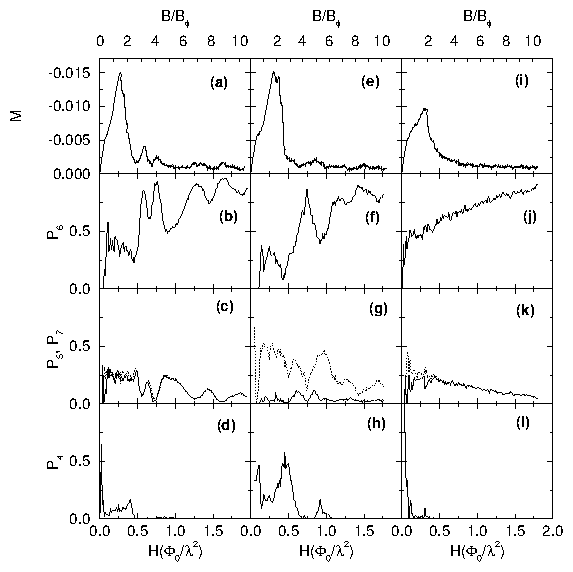
 Figure 3:
Magnetization M(H) and the fraction of vortices with coordination
number k, Pk(H), for triangular (a-d), square (e-h), and random
(i-l),
arrays of pins with the same pinning parameters as found in Figs. 1 and 2.
In (c) and (g), P5 (P7) is represented with a dotted (solid) line.
In (a) peaks in M(H) can be seen at the 3rd, 4th, 7th and 9th MFs,
which coincide with peaks in P6(H) shown in (b). For the square
pinning, small peaks are seen in M(H), (e), at the 2nd, 4th,
5th and 8th MFs.
The 4th and 5th (small) peaks merge near the 5th MF.
The peaks in P6, (f), indicate that the VL is
triangular at the 4th, 6th and 8th MFs, while peaks in P4,
(h), indicate that the VL is square at the 2nd and 5th MFs.
Sometimes, the peak is slightly shifted
(e.g. to 2.5 instead of 2 or 4.5 instead of 4) because of
the gradient in the fields.
In (g) P5 is the upper curve, while in (c) and (k)
P5 and P7 follow each other.
For
the random pinning array at low fields
the maximum value |M(H)| is 0.0095 Φ0/λ2,
about 1.5 times less than the triangular or square pinning arrays (a,b).
For H > 0.4 Φ0/λ2,
the magnetization M(H) falls off smoothly while
P6 slowly increases as vortex-vortex interactions dominate at
higher fields.
Figure 3:
Magnetization M(H) and the fraction of vortices with coordination
number k, Pk(H), for triangular (a-d), square (e-h), and random
(i-l),
arrays of pins with the same pinning parameters as found in Figs. 1 and 2.
In (c) and (g), P5 (P7) is represented with a dotted (solid) line.
In (a) peaks in M(H) can be seen at the 3rd, 4th, 7th and 9th MFs,
which coincide with peaks in P6(H) shown in (b). For the square
pinning, small peaks are seen in M(H), (e), at the 2nd, 4th,
5th and 8th MFs.
The 4th and 5th (small) peaks merge near the 5th MF.
The peaks in P6, (f), indicate that the VL is
triangular at the 4th, 6th and 8th MFs, while peaks in P4,
(h), indicate that the VL is square at the 2nd and 5th MFs.
Sometimes, the peak is slightly shifted
(e.g. to 2.5 instead of 2 or 4.5 instead of 4) because of
the gradient in the fields.
In (g) P5 is the upper curve, while in (c) and (k)
P5 and P7 follow each other.
For
the random pinning array at low fields
the maximum value |M(H)| is 0.0095 Φ0/λ2,
about 1.5 times less than the triangular or square pinning arrays (a,b).
For H > 0.4 Φ0/λ2,
the magnetization M(H) falls off smoothly while
P6 slowly increases as vortex-vortex interactions dominate at
higher fields.
|
