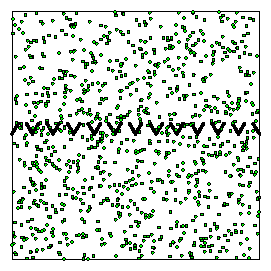
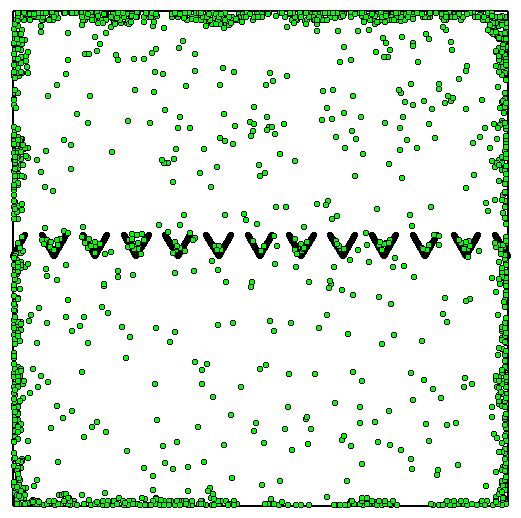
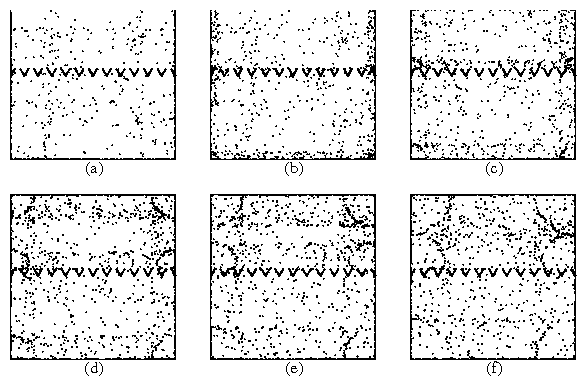
 Figure 11:
The formation of moving particle fronts for a system with Rule I,
no steric interactions, lr = 80, and synchronized tumbling times, shown
as consecutive snapshots of the system taken at equal time intervals.
The particles accumulate in the corners of the container and are
released as a semicircular density wave after each switching event.
Figure 11:
The formation of moving particle fronts for a system with Rule I,
no steric interactions, lr = 80, and synchronized tumbling times, shown
as consecutive snapshots of the system taken at equal time intervals.
The particles accumulate in the corners of the container and are
released as a semicircular density wave after each switching event.
|