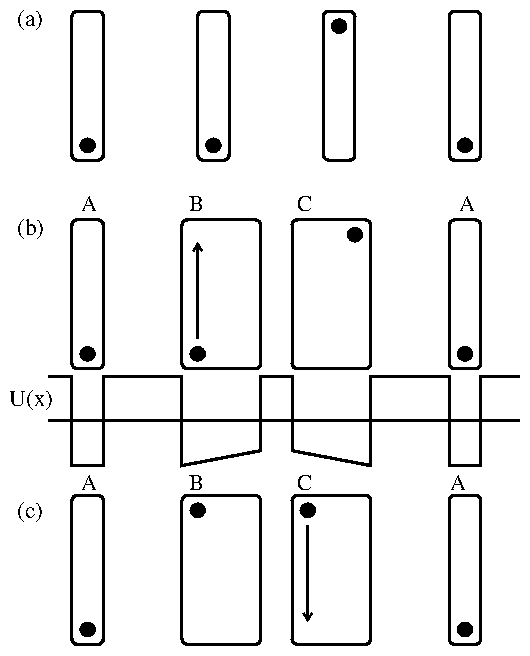
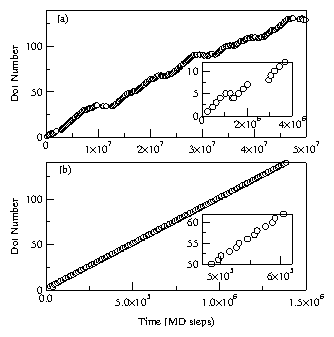
 Figure 2: Simulated signal propagation through a pipeline. The time at which
the vortex in each well changes states is indicated. (a) Thermally
activated ratchet operating at T=0.5.
Inset: Detail of the occasional backward and nonpropagating motion
of the signal.
(b) Deterministic, perfectly clocked ratchet at T=0.
Inset: Detail showing the slight
asymmetry in switching times of the three wells.
Figure 2: Simulated signal propagation through a pipeline. The time at which
the vortex in each well changes states is indicated. (a) Thermally
activated ratchet operating at T=0.5.
Inset: Detail of the occasional backward and nonpropagating motion
of the signal.
(b) Deterministic, perfectly clocked ratchet at T=0.
Inset: Detail showing the slight
asymmetry in switching times of the three wells.
|