Physical Review E 71, 062403 (2005)

Ordering and Melting in Colloidal Molecular Crystal Mixtures

C. Reichhardt and C.J. Olson Reichhardt

Center for Nonlinear Studies and Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM 87545

(Received 4 December 2004; published 30 June 2005)

We show in simulations that a rich variety of novel orderings such as pinwheel and star states can be realized for colloidal molecular crystal mixtures at rational ratios of the number of colloids to the number of minima from an underlying periodic substrate. These states can have multi-step melting transitions and also show coexistence in which one species disorders while the other species remains orientationally ordered. For other mixtures, only partially ordered or frustrated states form.
Recently a new type of colloidal state termed colloidal molecular crystals (CMCs) for colloids interacting with two-dimensional periodic substrates has been proposed in simulations [1,2], observed experimentally [3], and studied theoretically [4,5]. CMCs occur when the number of colloids is an integer multiple n of the number of substrate minima, and the n colloids residing in each minimum form a composite n-mer object such as a dimer or trimer. Neighboring n-mers can have an orientational ordering relative to one another in addition to the spatially periodic ordering imposed by the underlying substrate. The CMCs were named in analogy with molecular crystals, in which the molecules have orientational as well as crystalline ordering.
CMCs exhibit interesting two-step melting transitions. The first stage of melting occurs when the n-mers begin to rotate and lose orientational ordering, while in the second stage, the n-mers dissolve and individual colloids begin to diffuse throughout the sample [1,3]. The orientational melting was shown to fall into an Ising-like transition class [4,5]. A reentrant disordering can also occur in which an orientationally ordered n-mer state disorders when the substrate strength is increased [2,3]. Recent theoretical work has shown that the orientational ordering arises due to the anisotropic multipole interactions between the n-mers [4]. The reentrant disordering occurs when the n-mer is compressed by the increasing substrate force, decreasing both the distance between the colloids and the multipole moment, until the multipole interaction energy drops below the thermal energy.
When the substrate is varied, new states emerge. Studies of colloids interacting with arrays of small traps embedded in a smooth background have shown coexistence between an interstitial colloidal liquid and a pinned ordered solid [6]. In the case of colloids driven over two-dimensional (2D) substrates, interesting locking effects occur when the colloids move preferentially along certain symmetry directions of the underlying lattice [7,8,9,10]. Colloidal crystallization on periodic substrates may prove to be a useful method to create novel colloidal structures for photonic band gap device or filter applications [11]. Additionally, colloids are an ideal model system for studying collective particle states as well as topological defects generated on periodic substrates, which is relevant to a variety of other systems including atoms and molecules adsorbed on surfaces [12,13], superconducting vortices interacting with periodic pinning sites [14], or vortices in Bose-Einstein condensates interacting with periodic optical traps [15].
An open question is what kind of ordering and melting transitions occur for CMCs that are not pure, but are composed of a mixture of n-mers and m-mers, where m=n+1. In this work we show that when the number of colloids Nc is a rational, noninteger multiple p of the number of substrate minima Ns, a variety of novel crystalline and partially crystalline colloidal states form which cannot occur at integer fillings. These states include superlattices of n- and m-mer mixtures for certain values of p. As one example, we demonstrate pinwheel ordering similar to that observed for molecular dimers adsorbed on 2D atomic substrates. Other orderings, such as star shapes in which dimers point to a monomer, are also possible. These mixed states show a rich multi-step melting behavior in which the n-mers disorder one species at a time, followed by the dissolution of all of the n-mer states. The partially crystalline fillings may offer a convenient realization of an orientational glass [16].
We consider a 2D system of Nc colloids with periodic boundary conditions in the x and y directions, and employ Langevin dynamics as used in previous CMC simulations [1]. The equation of motion for a colloid i is
d ri
dt
 = ficc + fs + fT  .
(1)
Here ficc = −∑j ≠ iNc∇i V(rij) is the interaction force from the other colloids, where we assume a screened Coulomb interaction, V(rij) = (Q/|ri − rj|)exp(−κ|ri − rj|). Q=1 is the charge of the particles, 1/κ is the screening length, and ri(j) is the position of particle i(j). The substrate force comes from a triangular substrate such as that used in recent experiments [3], and is given by fs = ∑i=13Asin(2πbi /a0)[cos(θi)∧x − sin(θi)∧y], where bi=x cos(θi)−ysin(θi) + a0/2, θ1 = π/6, θ2 = π/2 and θ3 = 5π/5. Here A is the strength of the substrate. We measure length in units of the fixed substrate lattice constant a0, and take κ = 2/a0. We have also considered the case of square substrates. The thermal force fT is a randomly fluctuating force from random kicks. To obtain initial configurations, we start the system at a temperature where all the colloids are diffusing rapidly, and gradually cool to T = 0. In this model, we do not take into account hydrodynamic effects or possible long-range attractions between colloids. We focus on the regime where A is sufficiently large that the colloids are easily trapped. In the optical trap experiments, A can be readily tuned by varying the laser strength. We have checked our results for different system sizes and screening lengths and find no qualitative changes. To characterize the phases, we measure the finite time particle displacements δr = (1/Nc)∑i=1Nc|ri(t) − ri(t′)|, where t′ < t, as well as the fraction of six-fold coordinated colloids P6.
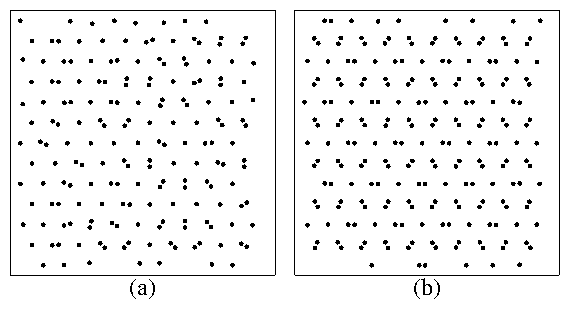
Fig1.png
Figure 1: The colloid configurations (black dots) at T = 0 for a triangular 2D periodic substrate with A = 2.5. (a) A filling of Nc/Ns=3/2, where a disordered or frustrated configuration occurs. (b) A filling of Nc/Ns=7/4, where a star ordering occurs.
We first consider mixtures of monomer and dimer colloid states, 1 < Nc/Ns < 2. Previous work has shown that a herringbone structure is stabilized at Nc/Ns = 2 (see Fig. 2(b) of Ref. [1]). At Nc/Ns = 3/2, illustrated in Fig. 1(a), we find a disordered arrangement of dimers and monomers. The system is frustrated since it is not possible to tile the triangular lattice with an alternating arrangement of monomers and dimers. Thus the monomer and dimer locations are disordered, and in addition, the dimers have only local orientational ordering. For Nc/Ns close to and including 3/2, the freezing temperature for dimer rotations is very low due to the lack of orientational order. In contrast, at Nc/Ns=7/4 we find an ordered state which we refer to as star ordering, shown in Fig. 1(b). Every other minimum in every other row captures a monomer while the remaining sites are occupied by dimers. All the dimers align such that they point toward the monomers, producing starlike structures. For Nc/Ns=7/4 the orientational disordering temperature, where the dimer orientational ordering is lost but the colloids remain localized, closely coincides with the orientational disordering temperature Tc of the herringbone state for Nc/Ns = 2.
The star state shown in Fig. 1(b) only occurs for sufficiently large A > 2.0. When the substrate is weaker, for 0.5 < A < 2.0, a pinwheel ordering occurs instead, in which the dimers surrounding the monomer have an additional tilt as illustrated in Fig. 2(a). There are two possible directions for this tilt and Fig. 2(a) shows the counterclockwise case; for different initial random seeds there is a 50% probability of producing a clockwise arrangement instead. Pinwheel states are predicted for the adsorption of dimer or linear molecules on triangular substrates at densities such that a portion of the dimers stand perpendicular to the surface, surrounded by the remaining dimers which lie parallel to the surface [12,13]. They can also occur for adsorbed atom-molecule mixtures such as CO(1−x)Arx [17]. Pinwheel states with a four-molecule basis are expected for a filling of 7/4 [12], and pinwheel states with a larger basis are also possible for higher fillings such as 13/7 [13]. For A < 0.5 at Nc/Ns=7/4, the colloid-colloid interactions begin to dominate over the substrate interaction and the colloids form an incommensurate modulated triangular lattice.
Fig2.png
Figure 2: (a) Colloid configuration (black dots) for filling of Nc/Ns=7/4 at A = 1.5, where a pinwheel state occurs. Two example pinwheels are highlighted with white circles and the rotational direction is marked with an arrow. (b) Colloid configuration for an orientationally frustrated filling of Nc/Ns=5/3 at A = 2.5. Local pinwheel ordering is indicated by the arrows. An example distorted pinwheel is highlighted with white circles.
By frustrating the system, we can create an orientationally disordered state. For example, in Fig. 2(b) we show a partially ordered state that occurs at a filling of Nc/Ns=5/3. Here, unlike the case in Fig. 1(a), there is positional ordering, since every third site in every row contains a monomer. The dimers, however, do not form an orientationally ordered arrangement, although locally the dimers have pinwheel or distorted pinwheel structures. Both chiralities of the pinwheels appear, as indicated in Fig. 2(b), but there is no long range dimer orientational ordering. At fillings Nc/Ns=5/4 and Nc/Ns=4/3, the dimers form a triangular lattice; however, since the spacing between neighboring dimers is larger than a0 in these configurations, the quadrupole-quadrupole interaction strength is too small to impose orientational order and the dimers are rotationally disordered even at very low temperatures.
Fig3.png
Figure 3: The colloidal positions (black dots) and trajectories (lines) over a fixed period of time for A = 3.0 and a filling of Nc/Ns=9/4 at different temperatures. (a) Phase I, trimer-dimer solid, at T/Tm = 0. (b) Phase II, trimer liquid, dimer solid phase, at T/Tm = 0.56. (c) Phase III, trimer-dimer liquid, at T/Tm = 2.4. (d) Modulated liquid phase, at T/Tm = 5.0.
For fillings 2 < Nc/Ns < 3, we obtain mixtures of dimers and trimers. At a filling of Nc/Ns=5/2 the dimer-trimer arrangement is positionally disordered since, similarly to the monomer-dimer case illustrated in Fig. 1(a), it is not possible to tile the underlying lattice alternately with dimers and trimers. At a filling of Nc/Ns=9/4 we find the ordered state shown in Fig. 3(a). Here the trimers form a triangular lattice where every other substrate minimum in every other row captures three colloids. In addition, the trimers are orientationally ordered, as are the dimers surrounding each trimer.
Since the Nc/Ns=9/4 dimer-trimer state has two different types of orientational order, we consider its melting properties to see whether the orientational ordering can be destroyed in more than one step. We find four phases as a function of temperature, illustrated in Fig. 3. We report temperature in units of Tm, the temperature at which the colloidal lattice at this density melts in the absence of the substrate. Phase I, the frozen orientationally ordered state described above, appears at low T, as shown in Fig. 3(a). As T increases, the trimers undergo a rotational disordering transition and begin to rotate at a temperature T(1)c; however, the dimers remain frozen. In Fig. 3(b) we plot the colloid trajectories (black lines) over a fixed time period for this phase, termed phase II, which shows that the trimers are undergoing rotation while the dimers are stationary and ordered. As T is further increased, the system enters phase III at T(2)c when a second orientational disordering transition occurs. Here the dimers lose their orientational order and begin to rotate, as illustrated in Fig. 3(c), but the colloids remain trapped within the substrate minima and there is no diffusion of colloids throughout the system. The trajectories of the rotating trimers are widened in Fig. 3(c) compared to Fig. 3(b) due to the higher temperatures. If the temperature is increased sufficiently, the dimers and trimers dissolve and diffusion occurs throughout the whole system in a modulated liquid, as shown in Fig. 3(d). Both the dimers and the trimers appear to dissolve at the same temperature, so we do not find an interstitial liquid of colloids moving throughout the sample coexisting with a pinned solid, such as seen in systems where the substrate has flat regions between traps [6,18].
Fig4.png
Figure 4: (a) The average displacement δr versus temperature for the system in Fig. 3. (b) Phase diagram for Nc/Ns=9/4 at different values of substrate strength A, showing the disordering lines between the different phases. Triangles: Tc(1), transition from phase I to phase II; squares: Tc(2), transition from phase II to phase III; circles: dissolution transition from phase III to a modulated liquid (ML).
The transitions between the different phases can be observed by monitoring the average particle displacements δr. In Fig. 4(a) we plot δr vs T/Tm for the system from Fig. 3. Here, δr=0 in phase I. The transition to the trimer liquid, dimer solid phase II appears as a step in δr at Tc(1), while a second step occurs at Tc(2) at the transition to the dimer-trimer liquid phase III. In the modulated liquid phase δr increases rapidly. Note that although there are sharp jumps in δr, these are not signatures of a first order transition but instead arise due to our definition of the measure. We have used δr to identify the transitions between the phases in a series of simulations for different substrate strengths A at Nc/Ns=9/4. We consider only A > 1, since at this filling for A < 1 new incommensurate modulated triangular ordering states appear as the colloid-colloid interactions become dominant. As indicated in Fig. 4(b), the transition temperatures T(1)c and T(2)c both decrease as A increases, with Tc(1) decreasing more rapidly than Tc(2). In contrast, the crossover line from phase III to the modulated liquid increases linearly with A. In simulation [1] and experiments [3] on single-species CMCs, the transition temperature from the oriented CMC state to the orientationally disordered CMC state decreases with increasing substrate strength, as also seen here for the multi-species CMC. Theoretical work for the single species case [4] has shown that this is due to the reduction of the effective multipole moments when the colloids in each substrate minimum are forced closer together with increasing A. In phase I of the multi-species case, the long range orientational order of the trimers arises due to interactions with the other trimers. Because the average trimer-trimer spacing is much larger than the average dimer-dimer spacing, the trimer orientational ordering energy is smaller than the dimer orientational energy and thus the trimers undergo a rotational disordering transition at a lower temperature than the dimers. We note that similar multi-step melting transitions occur for other filling fractions whenever both n- and m-mer species have orientational ordering at low temperatures.
In conclusion, we have shown that in colloidal molecular crystals composed of monomer-dimer or dimer-trimer mixtures, a rich variety of novel ordered and partially ordered states can occur. The ordered monomer-dimer states include star and pinwheel states, where the latter are similar to phases observed for molecular dimers adsorbed on periodic substrates. Unlike the molecular system, it is possible to observe the colloidal versions of these phases directly in experiment, and in addition the strength of the quadrupole interaction between dimers can be tuned by varying the substrate strength. For other monomer-dimer fillings, partially ordered or frustrated states can occur, including a positionally ordered but orientationally disordered state which may offer a convenient realization of an orientational glass. For ordered states in which the two species both have orientational ordering, such as dimer-trimer mixtures, a multi-step melting occurs where one species rotationally disorders while the other species remains orientationally ordered. As the temperature increases further, the second species loses its orientational order and finally at high temperatures the n-mer states dissociate into a modulated liquid. In addition to colloids on periodic substrates, similar states may be realizable for vortices in superconductors with periodic pinning or for vortices in Bose-Einstein condensates interacting with periodic substrates.
We thank C. Bechinger for useful discussions. This work was supported by the U.S. Department of Energy under Contract No. W-7405-ENG-36.

References

[1]
C. Reichhardt and C.J. Olson, Phys. Rev. Lett. 88, 248301 (2002).
[2]
M. Mikulis, C.J. Olson Reichhardt, C. Reichhardt, R.T. Scalettar, and G.T. Zimányi, J. Phys: Condens. Matter 16, 7909 (2004).
[3]
M. Brunner and C. Bechinger, Phys. Rev. Lett. 88, 248302 (2002).
[4]
R. Agra, F. van Wijland, and E. Trizac, Phys. Rev. Lett. 93, 018304 (2004), and to be published.
[5]
A. Sarlah, T. Franosch, and E. Frey, to be published.
[6]
K. Mangold, P. Leiderer, and C. Bechinger, Phys. Rev. Lett. 90, 158302 (2003).
[7]
P.T. Korda, M.B. Taylor, and D.G. Grier, Phys. Rev. Lett. 89, 128301 (2002).
[8]
M.P. MacDonald, G.C. Spalding, and K. Doholakia, Nature (London) 426, 421 (2003).
[9]
A. Gopinathan and D.G. Grier, Phys. Rev. Lett. 92, 130602 (2004); K. Ladavac, K. Kasza, and D.G. Grier, Phys. Rev. E 70, 010901(R) (2004); M. Pelton, K. Ladavac and D.G. Grier, ibid. 70, 031108 (2004).
[10]
C. Reichhardt and C.J. Olson Reichhardt, Europhys. Lett. 68, 303 (2004).
[11]
K. Dholakia, G.C. Spalding, and M.P. MacDonald, Physics World 15, 31 (2002); D.G. Grier, Nature (London) 424, 810 (2003).
[12]
A.B. Harris and A.J. Berlinsky, Can. J. Phys. 57, 1852 (1979); M. Schick, Surf. Sci. 125, 94 (1983); J. Belak, K. Kobashi, and R.D. Etters, ibid. 161, 390 (1985); H. You, S.C. Fain, S. Satija, and L. Passell, Phys. Rev. Lett. 56, 244 (1986); E.J. Nicol, C. Kallin, and A.J. Berlinsky, Phys. Rev. B 38, 556 (1988); S.E. Roosevelt and L.W. Bruch, ibid. 41, 12236 (1990); C. Ramseyer et al., ibid. 58, 4111 (1998).
[13]
P. Zeppenfeld et al., Phys. Rev. Lett. 78, 1504 (1997); B. Leinböck, B. Krömker, H. Wiechert, and M. Hofmann, ibid. 84, 1954 (2000).
[14]
M. Baert, V.V. Metlushko, R. Jonckheere, V.V. Moshchalkov, and Y. Bruynseraede, Phys. Rev. Lett. 74, 3269 (1995); J.I. Martín, M. Velez, J. Nogues, and I.K. Schuller, ibid. 79, 1929 (1997); C. Reichhardt, C.J. Olson, and F. Nori, Phys. Rev. B 57, 7937 (1998); B.J. Baelus, L.R.E. Cabral, and F.M. Peeters, ibid. 69, 064506 (2004).
[15]
J.W. Reijnders and R.A. Duine, Phys. Rev. Lett. 93, 060401 (2004); H. Pu, L.O. Baksmaty, S. Yi, and N.P. Bigelow, cond-mat/0404750.
[16]
K. Binder and J. Reger, Adv. Phys. 41, 547 (1992).
[17]
H. Wiechert and K.-D. Kortmann, Surf. Sci. 441, 65 (1999).
[18]
C. Reichhardt, C.J. Olson, R.T. Scalettar, and G.T. Zimányi, Phys. Rev. B 64, 144509 (2001).


File translated from TEX by TTHgold, version 4.00.

Back to Home