Europhysics Letters 68, 303 (2004)

Dynamic Regimes and Spontaneous Symmetry Breaking for Driven Colloids on Triangular Substrates

C. Reichhardt and C.J. Olson Reichhardt

Center for Nonlinear Studies and Theoretical Division, Los Alamos National Laboratory
Los Alamos, NM 87545, USA

recieved 8 July 2004; accepted 17 August 2004

PACS. 82.70.Dd - Colloids.
PACS. 05.70.Ln - Nonequilibrium and irreversible thermodynamics.
PACS. 05.60.Cd - Classical transport.
Abstract. - For collectively interacting repulsive colloids driven on triangular substrates, we show that a number of distinct dynamical regimes arise as a function of the drive strength. Additionally we show that for certain directions of drive a spontaneous symmetry breaking phenomenon occurs where all the colloids can flow in one of two directions that are not aligned with the external drive. Along these directions, the flow is highly ordered, in contrast to the disordered flow that occurs when the colloids move in the direction of the drive. We also find unusual hysteretic properties that arise due to the symmetry breaking properties of the flows.
A wide variety of systems can be represented as collectively interacting particles moving over an underlying periodic substrate, including atomic friction [1] and driven vortices in superconductors with periodic arrays of pinning sites [2,3,4,5]. In these systems a rich variety of dynamical regimes and transitions between the regimes can occur with increasing applied drive. These regimes include highly disordered fluctuating flows as well as ordered one-dimensional (1D) and 2D flows. In some cases there is hysteresis in the velocity-force curves when the applied drive is increased and subsequently decreased [1,3]. Usually the average velocity is finite in the direction of the applied force but zero in the direction transverse to the applied force. In certain situations, however, the particle flow locks to a symmetry direction of the underlying lattice rather than to the direction of the applied drive, since the particles can more effectively channel along a symmetry direction. This symmetry locking effect has been specifically demonstrated in simulations of vortices moving over a 2D square periodic substrate where the angle of the drive is varied with respect to the substrate [6]. A series of locked regimes occur in the form of plateaus in the velocity vs angle curve, giving a devil's staircase structure [6]. This locking effect has also been seen in experiments for vortices in superconductors with periodic arrays [5]. Similar symmetry locking effects have been proposed for classical electrons driven over 2D periodic substrates [7].
Another example of interacting particles on a periodic substrate which has recently been experimentally realized is colloids interacting with a periodic optical lattice substrate. Experiments and simulations have shown that a variety of novel colloidal crystalline states occur in this geometry [8,9,10,11], while colloids driven over 2D periodic arrays have also recently been studied in experiments [12,13] and theory [14]. In particular the previously predicted symmetry locking effects [6,7] were observed as the relative angle between the colloidal flow direction and the periodic substrate changed. These locking effects may be very valuable as a method for sorting different species of colloids when one species locks to a symmetry direction of the pinning lattice while the other species does not, so that over time the species can be separated in the transverse direction.
Fig1.png
Figure 1: Schematic of the system with a triangular substrate. The potential minima are at the center of the circles. Each minima captures one or more interacting colloids. The applied driving force is fd ∧y (solid arrow). There are two easy flow directions at ±30° from the drive (dashed arrows).
Even though numerous experiments exist for colloids moving over periodic substrates, numerical simulations for this system have not been performed until now. Here we demonstrate a realization of two degenerate symmetry locking directions for colloids moving over a periodic substrate. When there are many interacting driven colloids moving on a triangular lattice oriented such that the applied drive is between two pronounced symmetry directions, as illustrated schematically in Fig. 1, a global dynamical spontaneous symmetry breaking can occur where all the colloids organize to flow along one of the two symmetry directions rather than in the direction of drive. We emphasize that this transition is driven by collective interactions between the colloids; in the limit of a single colloid at finite temperature, symmetry breaking does not occur. When the global flow is along one of the substrate symmetry directions, the flow is ordered with few fluctuations and the colloid spacing is uniform, reducing the interaction energy. If the global flow is instead along the direction of the drive, the colloid configurations and flow are highly disordered. For different initial conditions, the symmetry breaking is equally likely to occur in either direction; thus, for an ensemble of realizations, the symmetry is restored in the statistical sense. The symmetry breaking is lost when the applied drive is large enough to force the colloids to move in the direction of drive or when the temperature is large enough to melt the ordered lattice. Additionally we find a series of distinct dynamical regimes similar to those observed for driven vortices in periodic pinning arrays [3]. Interestingly, some of these flow regimes effectively erase the memory of the system, which can lead to unusual hysteresis effects. For example, when the drive is increased, the colloids may lock to the +30° direction at low drives, but if the system passes through a disordered flow regime at high drives, the memory of the locking direction is lost; thus, when decreasing the drive back into the locking regime, the flow has an equal probability to lock to the +30° or −30° directions. Finally, we argue that the locking effect only occurs for finite size systems.
We consider a system of Nc overdamped repulsively interacting colloids on an underlying triangular periodic substrate with N minima. The equation of motion for a colloid i is
d ri
dt
 = fcci +fs + fd + fT  .
(1)
The colloid-colloid interaction force is fcci = −∑j ≠ iNc∇i V(rij), where we use a Yukawa or screened Coulomb interaction potential appropriate for colloids, given by V(rij) = (q2/|ri − rj|)exp(−κ|ri − rj|). Here q is the colloid charge, 1/κ is the screening length, and ri(j) is the position of particle i (j). Length is measured in units of the substrate lattice constant a0 and we take κ = 3/a0. The force from a triangular substrate is fs = ∑i=13Asin(2πpi/a0)[cos(θi)∧x − sin(θi)∧y], where A=3, pi = xcos(θi) − ysin(θi) + a0/2, θ1 = π/6, θ2 = π/2, and θ3 = 5π/6. Such a substrate can capture multiple colloids per minima, as demonstrated in recent experiments on colloidal crystalline states with up to three colloids per trap [9]. The dashed arrows in Fig. 1 indicate the symmetry directions for colloid flow. The thermal force fT is a randomly fluctuating force from Langevin kicks, and we consider both T = 0 and finite T. The initial colloidal positions are obtained by simulated annealing from a high temperature. The driving force fd, applied in the y direction as shown in Fig. 1, is increased in small increments to a finite value and then similarly decreased back to zero. We measure both the velocity in the direction of drive, Vy = ∑iNvi·∧y, and the velocity transverse to the drive, Vx = ∑iNvi·∧x.
Fig2.png
Figure 2: (a) Velocity in the direction of drive Vy vs applied drive fd for a system of interacting colloids on a triangular substrate for Nc/N = 1.39. (b) Corresponding transverse velocity Vx vs fd. Regions I-IV correspond to different particle flow regimes. (c) The transverse velocity Vx vs fd for slightly different initial conditions showing that the transverse velocity reverses from (b).
We concentrate on a regime where the number of colloids is greater than the number of potential minima, Nc/N > 1, as in recent experiments on triangular substrates [9]. In Fig. 2(a) we plot the average particle velocity in the direction of the drive, Vy, vs applied force for a system with Nc/N = 1.39. In Fig. 2(b) we show the corresponding average velocity in the x-direction, Vx. Here four distinct dynamic regions can be observed. The first region, I, is the pinned regime where particles do not move in either direction. Region II is the spontaneous symmetry breaking regime where the global flow of particles follows either the positive or negative 30° direction as in Fig. 1. In this regime Vy and Vx both increase linearly with increasing fd. In Fig. 2(b) the particles flow along −30°, producing a negative Vx or Hall current. As fd increases, the particles start to move in the direction of the drive and there is a transition to region III flow. This transition appears as a sharp drop in Vx with a corresponding increase in the slope of Vy. Region III is a disordered flow regime with zero average flow in the x-direction. At higher drives we find a crossover to a more ordered flow in Region IV, which can be identified by the reduction of fluctuations in Vy. In region IV there can be a slight initial drift in the x direction due to the orientation of the moving particle lattice with respect to the triangular substrate, but as fd further increases, Vx goes to zero.
In Fig. 2(c) we show Vx for the same system as in Fig. 2(a,b) but with slightly different initial particle positions. Here the curve appears almost the same as in Fig. 2(b), but the flow in region II is in the positive x-direction. We find such symmetry breaking flow, which is equally likely to be in the positive or negative direction, for fillings Nc/N > 1.0. There is a small region below the onset of region II where the flow shifts transiently between the positive and negative directions before it locks to one of the directions.
We have simulated larger systems with fixed parameters and find the same type of velocity-force curves. The depinning threshold is independent of size, as is the onset of region III. The transitory time ttr for the flow to organize into region II increases with system size as ttr  ∼ N0.6. In the larger systems, different parts of the system move in different directions and a coarsening process must occur for one direction to dominate. This implies that, in an infinite system, the time for one direction of flow to dominate will be infinite. Any experimental system, however, will be of small enough size for the symmetry breaking to be observable.
At Nc/N = 2 and 3 and T = 0, region II does not occur because the particle configurations are completely ordered at these commensurate fillings and there are no perturbations to knock the system into one of the symmetry directions of the lattice. At finite temperatures, however, region II reappears for these fillings. At incommensurate fillings there is a symmetry breaking due to the positional disorder of the particles. For fillings 1.0 < Nc/N < 2.0 the velocity force curves look very similar to the curves shown in Fig. 2. For Nc/N > 2.0, region II can still occur; however, additional dynamical regimes arise which appear as features in the velocity force curves and the noise fluctuations.
Fig3.png
Figure 3: Colloid positions (white dots) and trajectories (black lines) for the system in Fig. 2. (a) Pinned region I, fd = 0. (b) −30° symmetry breaking flow at fd = 1. (c) +30° symmetry breaking flow at fd = 1. (d) Disordered flow in region III, fd = 3.2.
In Fig. 3 we plot the colloidal positions and trajectories for the different regimes. Fig. 3(a) shows the pinned regime for the system in Fig. 2, where a portion of the sites capture two or more colloids. In Fig. 3(b) region II is shown for Fig. 2(b) at fd = 1.0, with the particles moving in 1D paths along −30°. In Fig. 3(c), the case for Fig. 2(c) is shown for the same fd with the flow along +30°. Fig. 3(d) illustrates region III flow from Fig. 2(c) at fd = 3.2, where the particle positions and trajectories are disordered. Region IV flow at higher fd is much more ordered and the particles move mostly straight along the y direction; however, there are still some dislocations which cause the trajectories to be partially disordered.
The region II flow can be regarded as an example of spontaneous symmetry breaking. There is no asymmetry across the x-axis and in any given realization the system is equally likely to lock to either +30° or −30°. Spontaneous symmetry breaking is not limited to equilibrium systems. In condensed matter, the most familiar example is that of a ferromagnet in zero external field where there are two energy minima. A small perturbation from temperature or dynamics biases the system in one direction or another. In our system, when the flow follows one of the symmetry directions, the flow is more ordered and the particle spacing is more uniform.
We have also considered a single particle for the system in Fig. 1 as well as other fillings with Nc/N < 1.0. In these cases the global flow locking does not occur. This is due to the lack of interactions at these low fillings. At depinning, each particle can move in either the positive or negative direction at each potential maximum. If there are no neighboring particles blocking one of the routes, the particle flows in a random zig-zag pattern.
Some of the features in the velocity force curves in Fig. 2 can be understood by force balance arguments. For the commensurate case Nc = N, the colloid configurations are completely symmetric and the interaction forces are zero, so depinning occurs at fd = A, the maximum force from the substrate. For higher Nc, some substrate minima capture more than one colloid. In these dimerised phases, a colloid feels an additional force from the other colloid in the same minima. This will reduce the force needed to depin the colloids by the interaction force fij(a0/2). Using our parameters this would give a depinning force of 0.8 which is somewhat higher than the measured value due to the collective interactions of many dimers. Fig. 3(a) shows that the dimerised states preferably orient either in the positive or negative 30° direction, so that is the direction in which they depin. The transition to region IV flow occurs for fd > A where the colloids can move freely over the substrate potential maxima.
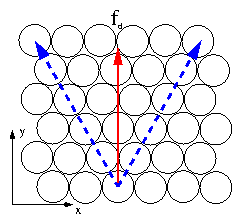
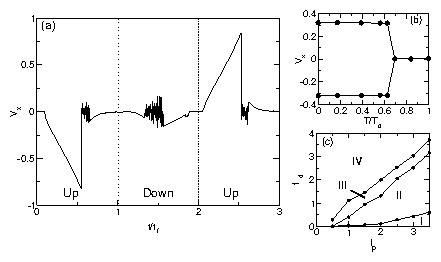
Fig4.png
Figure 4: (a) The transverse velocity Vx for the ramp up phase of 0.0 < fd ≤ 4.8 for time 0 < t/tr < 1; down from fd = 4.8 to 0, 1 < t/tr < 2; and up again to fd = 4.8, 2 < t/tr < 3. Here tr=2.24 ×106 molecular dynamics time steps. (b) Transverse velocity for fixed fd=1.0 vs T/Td. (c) The different flow regimes for fd vs fp.
We next consider the hysteretic properties of the regimes by performing simulations where the external drive is cycled up, down, and up again. In Fig. 4(a) we show the results for the same system as in Fig. 2 for three drive cycles. For 0 < t/tr < 1 where tr=2.24 ×106 molecular dynamics time steps, fd is increased from zero to fd = 4.8. On the ramp down, beginning at t/tr=1, there is clear hysteresis in the III-II transition with region III persisting longer on the downward sweep. Hysteresis across the II-III crossover is consistent with the first order-like sharp jump in Vx across the II-III crossover. On the ramp down, region II is again in the negative direction. The slope is also smaller as there are more commensurate pinned rows. We note that because the system goes through region III the flow is disordered so that the pinned regime near the end of the ramp down phase is not necessarily the same as the initial pinned regime. On the next ramp up, beginning at t/tr=2, Vx in region II reverses and is in the positive direction. For continued cycling, even at T = 0, the direction of the region II flow falls randomly in either direction. This is due to the dynamical disordering introduced by the region III flow, which destroys the memory of the previous pinned regime. We observe similar hysteresis effects for other fillings in the range 1 < Nc/N < 4.
We have also studied the temperature dependence of the regimes in Fig. 2. We find that region II ends at a sharp crossover temperature of Tc=0.7 Td, where Td is the onset temperature for particle diffusion at fd = 0. In Fig. 4(b), we plot Vx for fixed fd=1.0 as a function of temperature showing the two branches of the velocity flow up to Tc. The sharp loss of region II as a function of T is consistent with the sharp crossover from region II to the disordered region III. Hysteresis effects also vanish at Tc. The flow regimes and the general shape of the velocity force curves are very similar at finite temperatures up to 0.6Td. The temperature induces some smearing of the velocity force curves.
We next consider the effect of the substrate strength on the flow regimes. In Fig. 4(c) we plot locations of the different flow regions for fd vs fp for the same system in Fig. 4(a). Here fp must exceed a minimum value in order for the region II flow to occur, since for weak substrates the colloids form a more triangular lattice rather than the dimer states. The width of the symmetry breaking region is enhanced for larger fp.
Finally, we note that the symmetry breaking property of the system may be a good way to test the order in an experimental array. For example, if an experiment is performed repeatedly and one direction is favored every time, than some form of disorder may be responsible. Since the experiments typically employ optical traps in which the laser intensity in both the x and y directions can be carefully controlled, it should be possible to add a small intensity shift to counter any bias effects.
To summarize, we find a novel spontaneous symmetry breaking phenomenon for collectively interacting driven colloids on triangular substrates. A series of distinct flow regimes occur including a spontaneous symmetry breaking flow where global particle flow occurs along one of two symmetry directions of the underlying lattice and not in the direction of the applied drive. The flow along the symmetry directions is much more ordered than the flow in the direction of the drive. The symmetry breaking combined with the flow transverse to the drive produces interesting hysteresis phenomena in the transverse velocity curves where the colloids may lock to different directions upon increasing and decreasing the drive, as long as the particles pass through a disordered flow regime. The results in this work can be realized for colloids driven over optical trap arrays and vortices in superconductors with periodic pinning arrays. Similar effects may be possible for atomic friction systems.
This work was supported by the U.S. DoE under Contract No. W-7405-ENG-36.

References

[1]
Persson B.N.J., Phys. Rev. Lett. 71 (1993) 1212; Braun O.M., Dauxois T., Paliy M.V. and Peyrard M., Phys. Rev. Lett. 78 (1997) 1295; Granato E. and Ying S.C., Phys. Rev. Lett. 85 (2000) 5368.
[2]
Baert M., Metlushko V.V., Jonckheere R., Moshchalkov V.V. and Bruynseraede Y., Phys. Rev. Lett. 74 (1995) 3269; Harada K., Kamimura O., Kasai H., Matsuda T., Tonomura A. and Moshchalkov V.V., Science 274 (1996) 1167; Martín J.I., Velez M., Hoffmann A., Schuller I.K. and Vicent J.L., Phys. Rev. Lett. 83 (1999) 1022.
[3]
Reichhardt C. and Olson C.J., Phys. Rev. Lett. 88 (2002) 248301.
[4]
Reichhardt C., Olson C.J. and Nori F., Phys. Rev. B 58 (1998) 6534; Zhu B.Y., Van Look L., Moshchalkov V.V., Zhao B.R. and Zhao Z.X., Phys. Rev. B 64 (2001) 012504; Reichhardt C., Zimányi G.T. and Grønbech-Jensen N., Phys. Rev. B 64 (2001) 014501.
[5]
Silhanek A.V., Van Look L., Raedts S., Jonckheere R., and Moshchalkov V.V., Phys. Rev. B 68 (2003) 214504; Villegas J.E., Gonzalez E.M., Montero M.I., Schuller I.K., and Vicent J.L., Phys. Rev. B 68 (2003) 224504.
[6]
Reichhardt C. and Nori F., Phys. Rev. Lett. 82 (1999) 414.
[7]
Wiersig J. and Ahn K.-H., Phys. Rev. Lett. 87 (2001) 026803.
[8]
Korda P.T., Spalding G.C. and Grier D.G. Phys. Rev. B 66 (2002) 024504.
[9]
Brunner M. and Bechinger C. Phys. Rev. Lett. 88 (2002) 248302.
[10]
Mangold K., Leiderer P. and Bechinger C., Phys. Rev. Lett. 90 (2003) 158302.
[11]
Gopinathan A. and Grier D.G., Phys. Rev. Lett. 92 (2004) 130602.
[12]
Korda P.T., Taylor M.B. and Grier D.G., Phys. Rev. Lett. 89 (2002) 128301.
[13]
MacDonald M.P., Spalding G.C. and Dholakia K., Nature 426 (2003) 421.
[14]
Ladavac K., Kasza K. and Grier D.G., cond-mat/0310396; Ladavac K., Pelton M. and Grier D.G., cond-mat/0404242.


File translated from TEX by TTHgold, version 4.00.

Back to Home