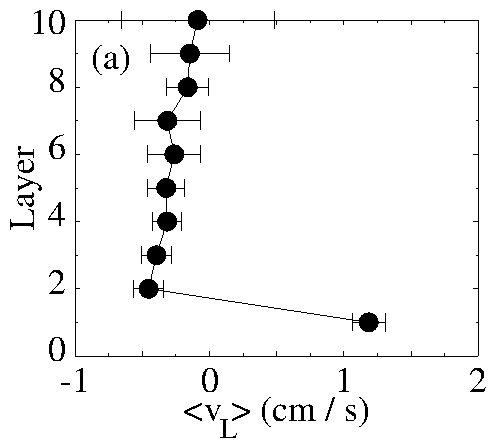
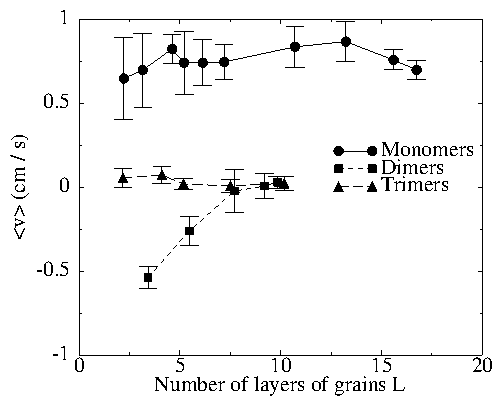
 Figure 2:
Average horizontal ratchet velocity 〈v〉 for monomer, dimer and
trimer grains as a function of the number of layers of grains L.
While monomers move to the right,
dimers move in the opposite direction.
Trimers are too massive to move at this driving amplitude.
As more and more layers of grains are added, all particles slow down,
with the heavier particles quenching first.
The downward trend of the monomer velocity continues with increased layers,
but these points are omitted from the graph due to space.
The sawteeth parameters were Ns = 16, hs = 1.25, and as = 0.0,
with driving at roughly 69 Hz and Ad = 0.75.
Figure 2:
Average horizontal ratchet velocity 〈v〉 for monomer, dimer and
trimer grains as a function of the number of layers of grains L.
While monomers move to the right,
dimers move in the opposite direction.
Trimers are too massive to move at this driving amplitude.
As more and more layers of grains are added, all particles slow down,
with the heavier particles quenching first.
The downward trend of the monomer velocity continues with increased layers,
but these points are omitted from the graph due to space.
The sawteeth parameters were Ns = 16, hs = 1.25, and as = 0.0,
with driving at roughly 69 Hz and Ad = 0.75.
|