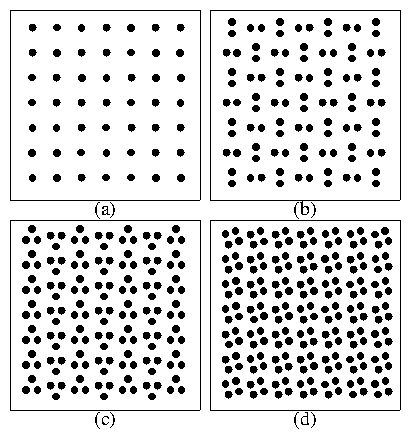
 Figure 1:
The colloid configurations
(black dots) at T = 0.0 for
a square 2D periodic substrate with A = 2.5, for
different densities of colloids.
(a) Nc=Nm.
The colloids form a square commensurate lattice.
(b) Nc=2Nm
forms
a colloidal dimer state, with each dimer perpendicular
to neighboring dimers.
(c) Nc=3Nm
forms a trimer state with orientational ordering.
(d) Nc=4Nm
produces an aligned quadrimer state.
Figure 1:
The colloid configurations
(black dots) at T = 0.0 for
a square 2D periodic substrate with A = 2.5, for
different densities of colloids.
(a) Nc=Nm.
The colloids form a square commensurate lattice.
(b) Nc=2Nm
forms
a colloidal dimer state, with each dimer perpendicular
to neighboring dimers.
(c) Nc=3Nm
forms a trimer state with orientational ordering.
(d) Nc=4Nm
produces an aligned quadrimer state.
|
