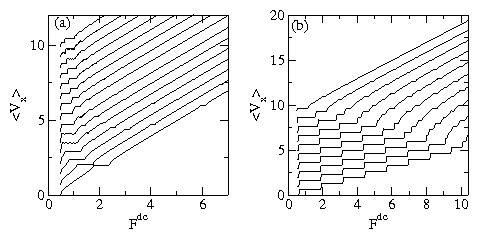
 Figure 1:
(a) 〈Vx〉 vs Fdc for a system with N/Np = 1
and Np=361 for
A=1 at varied flashing period.
From bottom to top,
Ts=100, 150, 200, 250, 300, 350, 400, 450, 500, 550, 600, 650, 700,
750, and 800 BD steps.
(b) Same as in (a), with a fixed Ts=300 and increasing substrate
strength A. From top to bottom, A=1, 2, 3, 4, 5, 6, 7, 8, 9,
and 10. All curves
have been vertically offset for
clarity.
Figure 1:
(a) 〈Vx〉 vs Fdc for a system with N/Np = 1
and Np=361 for
A=1 at varied flashing period.
From bottom to top,
Ts=100, 150, 200, 250, 300, 350, 400, 450, 500, 550, 600, 650, 700,
750, and 800 BD steps.
(b) Same as in (a), with a fixed Ts=300 and increasing substrate
strength A. From top to bottom, A=1, 2, 3, 4, 5, 6, 7, 8, 9,
and 10. All curves
have been vertically offset for
clarity.
|
