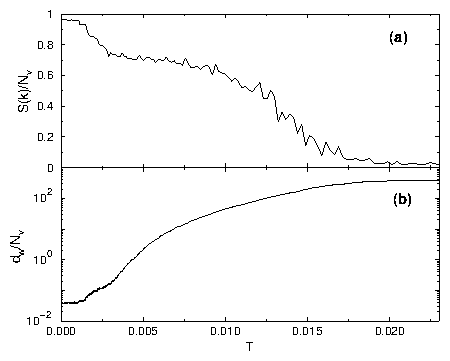
 Figure 1:
(a) The fraction of four-fold P4 (thick line)
and six-fold P6 coordinated (thin line) vortices
versus T. (b) The average power of the secondary peaks,
< S(k) > /Nv versus T.
The position of the peaks shifts from four-fold to six-fold near T = 0.001.
The peaks are lost at T = 0.005. The inset of (b) shows the scaling of the
secondary peaks for different system sizes where Nv ∼ L2. For the
pinned phase (circles), T = 0.0005 and S(k) ∼ L0;
for the triangular lattice (triangles), T = 0.003 and
S(k) ∼ L−0.33; and for the liquid phase (squares),
T = 0.007 and S(k) ∼ L−1.98. (c) The displacements
dw/Nv = < |r(T) − r(0)|2 >
of the vortices versus T.
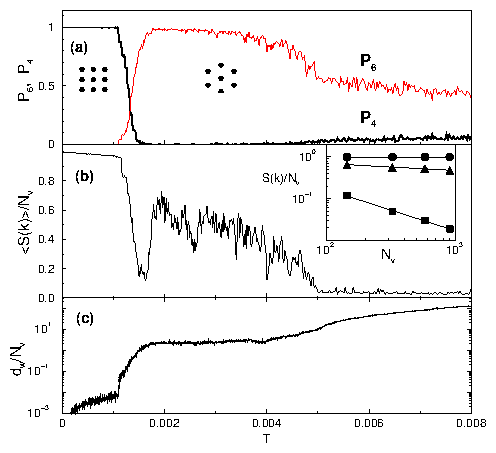
Figure 1:
(a) The fraction of four-fold P4 (thick line)
and six-fold P6 coordinated (thin line) vortices
versus T. (b) The average power of the secondary peaks,
< S(k) > /Nv versus T.
The position of the peaks shifts from four-fold to six-fold near T = 0.001.
The peaks are lost at T = 0.005. The inset of (b) shows the scaling of the
secondary peaks for different system sizes where Nv ∼ L2. For the
pinned phase (circles), T = 0.0005 and S(k) ∼ L0;
for the triangular lattice (triangles), T = 0.003 and
S(k) ∼ L−0.33; and for the liquid phase (squares),
T = 0.007 and S(k) ∼ L−1.98. (c) The displacements
dw/Nv = < |r(T) − r(0)|2 >
of the vortices versus T.
|