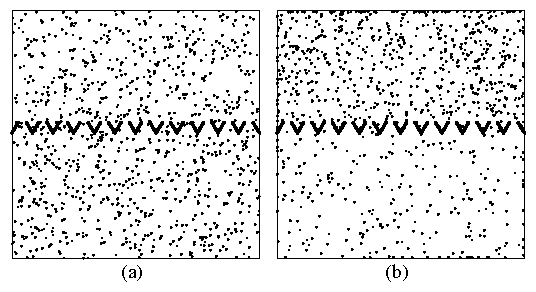
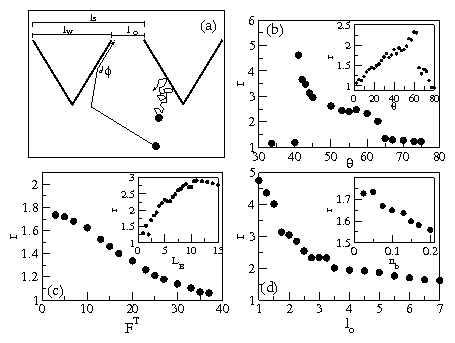
 Figure 4:
(a) Schematic trajectories for (dark line) a bacterium moving
under motor forces only and being entrained by the wall and
(light line) a bacterium experiencing only Brownian forces.
The
barrier spacing lS, opening
size lo,
funnel width lw,
and angle ϕ between the bacterium trajectory and the funnel barrier wall
are also indicated.
(b) r=ρ(1)/ρ(2) vs θ for a system with lb = 20,
FT=0,
fs=0, and L=99. Inset: r vs θ for the same system with fixed
lo=3.25 and varied L.
(c) r vs FT for a system with lb = 20, θ = 60°, L=99,
and fs=0. Inset: r vs LB for a system with lb=20, FT=0,
fs=0, fixed lo=3.25, and varied L.
(d) r vs lo for a system with lb=20, θ = 60°, LB=5.0,
fs=0, and varied L.
Inset: r vs overall bacteria
density ρb for a system with steric interactions,
fs=150, θ = 60°, fT=0, L=99, and lb = 20.
Figure 4:
(a) Schematic trajectories for (dark line) a bacterium moving
under motor forces only and being entrained by the wall and
(light line) a bacterium experiencing only Brownian forces.
The
barrier spacing lS, opening
size lo,
funnel width lw,
and angle ϕ between the bacterium trajectory and the funnel barrier wall
are also indicated.
(b) r=ρ(1)/ρ(2) vs θ for a system with lb = 20,
FT=0,
fs=0, and L=99. Inset: r vs θ for the same system with fixed
lo=3.25 and varied L.
(c) r vs FT for a system with lb = 20, θ = 60°, L=99,
and fs=0. Inset: r vs LB for a system with lb=20, FT=0,
fs=0, fixed lo=3.25, and varied L.
(d) r vs lo for a system with lb=20, θ = 60°, LB=5.0,
fs=0, and varied L.
Inset: r vs overall bacteria
density ρb for a system with steric interactions,
fs=150, θ = 60°, fT=0, L=99, and lb = 20.
|