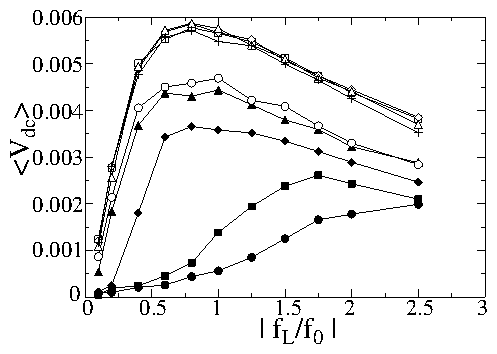
 Figure 5:
Rectified average fluxon velocity
〈v 〉,
which can be measured as a voltage,
versus the amplitude of the AC driving force.
The frequency of the AC signal is:
filled circles, ν = 1; filled squares, ν = 0.5;
filled diamonds, ν = 0.1; filled triangles, ν = 0.025;
open circles, ν = 0.0125; open squares, ν = 0.003125;
open diamonds, ν = 0.0021; open triangles, ν = 0.00104;
pluses, ν = 0.000521.
Figure 5:
Rectified average fluxon velocity
〈v 〉,
which can be measured as a voltage,
versus the amplitude of the AC driving force.
The frequency of the AC signal is:
filled circles, ν = 1; filled squares, ν = 0.5;
filled diamonds, ν = 0.1; filled triangles, ν = 0.025;
open circles, ν = 0.0125; open squares, ν = 0.003125;
open diamonds, ν = 0.0021; open triangles, ν = 0.00104;
pluses, ν = 0.000521.
|