Abstract
We examine the current driven dynamics for vortices interacting with
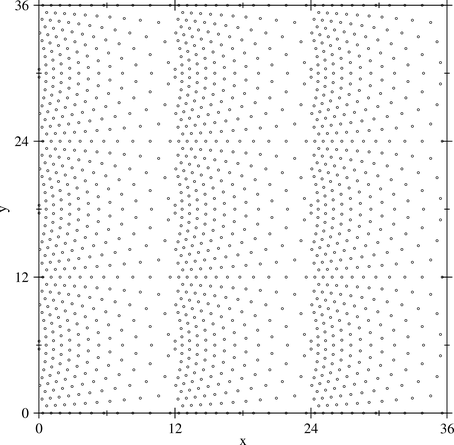
conformal crystal pinning arrays
and compare to the dynamics of vortices driven over random pinning
arrays. We find that the pinning is enhanced in the conformal
arrays for field densities less than 2.5 times the matching field.
At higher fields, the effectiveness of the
pinning in the moving vortex state is enhanced
in the random arrays compared to the conformal arrays, leading to
crossing of the velocity force curves.

|
| (1) |
| (2) |