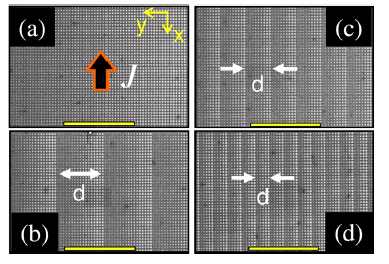
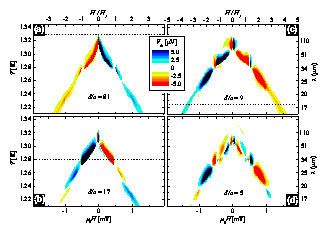
 Figure 2: (color online) Rectified signal Vdc as a function of field H and temperature T for samples with period of the asymmetric pinning potential (a) 162 μm, (b) 34 μm, (c) 18 μm, and (d) 10 μm corresponding to the images shown in Fig. 1. In all cases the external ac current is applied along the x axis. The horizontal dashed lines indicate the temperature at which λ ∼ d.
Figure 2: (color online) Rectified signal Vdc as a function of field H and temperature T for samples with period of the asymmetric pinning potential (a) 162 μm, (b) 34 μm, (c) 18 μm, and (d) 10 μm corresponding to the images shown in Fig. 1. In all cases the external ac current is applied along the x axis. The horizontal dashed lines indicate the temperature at which λ ∼ d.
|