Physica C 503, 52 (2014)

Comparing the Dynamics of Skyrmions and Superconducting Vortices

C.J. Olson Reichhardt^1,*, S.Z. Lin¹, D. Ray^1,2, and C. Reichhardt¹

¹Theoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA
²Department of Physics, University of Notre Dame, Notre Dame, Indiana 46556, USA

ARTICLE INFO
Article history.
Received 18 December 2013
Accepted 20 March 2014
Available online 28 April 2014

Keywords:
Superconducting vortex
Skyrmion
Pinning
Ratchet

ABSTRACT Vortices in type-II superconductors have attracted enormous attention as ideal systems in which to study nonequilibrium collective phenomena, since the self-ordering of the vortices competes with quenched disorder and thermal effects. Dynamic effects found in vortex systems include depinning, nonequilibrium phase transitions, creep, structural order-disorder transitions, and melting. Understanding vortex dynamics is also important for applications of superconductors which require the vortices either to remain pinned or to move in a controlled fashion. Recently, topological defects called skyrmions have been realized experimentally in chiral magnets. Here we highlight similarities and differences between skyrmion dynamics and vortex dynamics. Many of the previous ideas and experimental setups that have been applied to superconducting vortices can also be used to study skyrmions. We also discuss some of the differences between the two systems, such as the potentially large contribution of the Magnus force in the skyrmion system that can dramatically alter the dynamics and transport properties.

1. Introduction
2. Particle based simulations
3. Structure and dynamics
4. Transport
5. Discussion
6. Summary
References

1. Introduction

In a type-II superconductor in the presence of a magnetic field, flux enters the sample in the form of quantized units called vortices. In most cases vortices interact with each other via repulsive interactions, leading to the formation of a triangular lattice which is the lowest energy configuration [1,2]. When a current is applied to the sample, a Lorentz force acts on the vortices and causes them to move in a direction perpendicular to the applied current. Once the vortices are in motion, the material develops a finite resistance and a finite voltage response. In transport measurements, voltage-current curves can be used to study the vortex motion. In general, the sample contains some form of disorder that creates regions in which the superconducting order parameter is suppressed. These act as pinning sites for the vortices, holding the vortices immobile under an applied current up to the critical current at which the vortices depin [1,2]. For real-world applications, it is generally desirable to maximize the critical current, and numerous studies have addressed how to enhance the pinning in superconductors by various methods including ion irradiation [3] and the creation of tailored nanostructured pinning arrays [4,5,6]. On the basic science level, vortices have proven to be a very rich system for studying collective dynamics in the presence of random or periodic substrates. The depinning of vortices has been shown to exhibit properties of a nonequilibrium transition from a pinned disordered state to a dynamically fluctuating state [7], followed by a transition to a dynamical moving crystal [8] or moving smectic [9,10,11]. The vortex dynamics can be two-dimensional (2D), effectively 2D, or fully three-dimensional (3D), and the 3D systems can be anisotropic, such as in high temperature superconductors [2,12,13]. With various lithographic techniques it is possible to create periodic pinning potentials with different types of symmetry to trap the vortices [4,5,14,15,16,17,18,19,20,21]. In these structured pinning arrays, commensuration effects can occur when the number of vortices is an integer [4,5,14] or rational fractional [16,22] multiple of the number of pinning sites, and at the commensurate fields, different types of vortex crystal structures can be stabilized [5]. When the vortices are driven over the periodic arrays, a rich variety of dynamical effects can arise such as soliton type flows, dynamical ordering, and negative differential conductivity [23,24,25,26]. If some form of asymmetry is added to the pinning arrays, it is possible to create vortex ratchet effects in which an ac driving force induces a net dc motion of vortices [27,28,29,30]. There have also been proposals for novel flux logic devices where the vortices act as the information carriers [31].

Recently another type of emergent particle called a skyrmion has been discovered in condensed matter systems. Skyrmions were originally proposed as a model for baryons and mesons [32], and they were predicted to occur in condensed matter systems such as chiral magnets [33]. In 2008, triangular skyrmion lattices were observed via neutron scattering in chiral magnets [34], and soon after, a number of experiments using other types of imaging techniques revealed skyrmions in bulk and thin film samples [35]. The skyrmions can be stabilized more easily in thin films. It was also shown that skyrmions can be driven with an applied current which produces a Lorentz force on them, and that there can be a finite critical current required to set them in motion [36,37]. The small size of the skyrmion critical current has generated excitement since it could mean that skyrmions may have a significant advantage over magnetic domain walls in applications such as logic devices [36,38]. Skyrmion depinning has been studied in both continuum [39,40] and particle-based simulations [41].

Skyrmions appear to have many features in common with vortices in that they both minimize their repulsive interactions by forming a triangular lattice, can be driven with external currents, and exhibit a critical current for depinning. There are also several differences. For example, in skyrmions the Magnus term can be an important or even the dominant contribution to skyrmion motion, whereas in vortices the Magnus term is generally negligible. The strong effect of the Magnus force is conjectured to be responsible for the low critical current in the skyrmion systems [39,40]. Here we outline some of the similarities and differences in the particle based dynamics of skyrmions and vortices and also discuss how results found for vortex systems such as commensurations or ratchet effects could be realized in skyrmion systems.

2. Particle based simulations

Although vortices are extended objects with a core, in extreme type II superconductors they can be represented as pointlike or linelike objects, greatly facilitating numerical and theoretical studies of their electrodynamic properties. In an effective 2D model of pointlike vortices, a single vortex i undergoes motion described by the following equation of motion:

d R_i

= F^vv_i + F^P_i + F^D_i + F^T_i.

(1)

Here R_i is the location of vortex i, η = ϕ₀²d/2πξ²ρ_N is the damping constant, d is the sample thickness, ϕ₀ = h/2e is the elementary flux quantum, ξ is the superconducting coherence length, and ρ_N is the normal-state resistivity of the material. The vortex-vortex interaction force is F^vv_i = ∑^N_v_{j ≠ i}F₀K₁(R_ij/λ)∧R_ij, where K₁ is the modified Bessel function, λ is the London penetration depth, F₀ = ϕ₀²/(2πμ₀λ³), R_ij = |R_i − R_j| is the distance between vortex i and vortex j, and the unit vector ∧R_ij = (R − R_j)/R_ij. This form of vortex-vortex interaction is appropriate for 3D superconductors in which the vortex acts as a rigid object along its length. For thin film superconductors, the vortex-vortex interactions are much longer range and can be modeled with a logarithmic potential, F_i^vv=−∑_{j ≠ i}^N_v∇ V(R_ij) where V(R_ij) ∝ ln(R/λ) [22]. The force F^P from the pinning sites can be treated with various models; here, we consider parabolic attractive sites with

F^P_i = −

N_p
∑
k=1

(F_p/r_p)(R_i − R^(p)_k)Θ[(r_p − |R_i − R^(p)_i|)/λ].

(2)

where R^(p)_k is the location of pinning site k, F_p is the maximum pinning force, r_p is the pin radius, and Θ is the Heaviside step function. Langevin thermal kicks are applied using the term F^T_i which has the following properties: 〈F^T_i〉 = 0 and 〈F_i^T(t)F^T_j(t^′)〉 = 2ηk_BTδ_ijδ(t− t^′), where k_B is the Boltzmann constant. The driving force is from an externally applied current J resulting in a Lorentz force J ×B perpendicular to the applied current. It is also possible to use flux gradient driven simulations in which the vortices are added at one side of the sample and, through their own mutual repulsion, drive themselves though the sample [42]. When the vortices are pinned in the absence of creep, then even for a finite current the system is dissipationless and the voltage response is zero. Once the vortices are in motion, a finite voltage response develops that is proportional to the number of moving vortices and their velocity. If the external drive is applied in the x direction, the following quantity is proportional to the voltage: 〈V_x〉 = ∑^N_v_{i = 1}v_i·∧x, where v_i = dR_i/dt.

Additional dynamical terms such as a Magnus force can arise due to the interactions of the external current with currents circling around the vortices. This reduces the net current on one side of the vortex and enhances it on the other side. In most cases, for superconducting vortices the damping term is dominant so that the Magnus term is negligible [2].

The initial skyrmion simulations employed continuum models utilizing the Landau-Lifshitz-Gilbert equation [39,40], and showed that in the absence of disorder the skyrmions form a triangular lattice. Under an applied drive, the velocity versus applied force curves indicate that there is a depinning transition [39] as well as other phenomena at higher drives where the skyrmion lattice transitions into a chiral liquid state [40]. More recently, a particle-based model for skyrmions was proposed [41] inspired by Thiele's approach [43]. Here, the equation of motion is

αv_i = F_i^ss + F^P_i +F^M_i + F^L_i + F^T_i,

(3)

where v_i is the skyrmion velocity. The damping term α is due both to spin precession and conduction electrons localized in the core. The Lorentz force F^L = 2πħ e⁻¹ ∧z ×J arises due to the emergent quantized flux that occurs in the presence of a finite current. This term corresponds to the driving term in the vortex equation of motion. F^P is the force from the pinning sites and the Magnus term is F^M_i = β∧z ×v_i. By conducting continuum simulations where one skyrmion is brought close to a second immobilized skyrmion, we showed [41] that the skyrmion-skyrmion interaction force F^ss can be well approximated by K₁(r_d/ξ), where r_d is the distance between the skyrmions and ξ is the size of the core. Using typical parameters from MnSi, an estimation of the dissipative force per unit length is 5×10⁻⁶ N/m while the Magnus force is 5×10⁻⁵ N/m, indicating that the Magnus force will play an important role.

3. Structure and dynamics

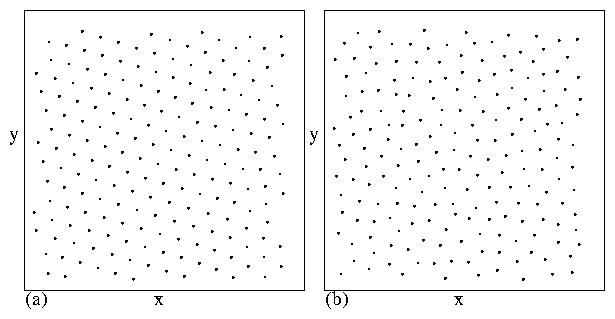Figure 1: Skyrmion positions (black dots) after simulated annealing. (a) A system without quenched disorder where the skyrmions form a triangular lattice. (b) A system with strong disorder shows a disordered or glassy structure.

For skyrmion dynamics, the relevant ratio is β/α, where β is the coefficient in front of the Magnus term and α is the damping term. In real experimental systems, this ratio can vary from 10 to 40. In Fig. 1(a) we show the skyrmion structure in the absence of disorder for a system containing N_s = 194 skyrmions with β/α = 10.0. The structure is obtained by slowly annealing from a high temperature state and cooling to T = 0. Here a triangular lattice appears similar to the triangular vortex lattice found in superconducting systems. In Fig. 1(b) we plot the skyrmion positions for the same system but with N_p = 100 non-overlapping pinning sites with maximum force F_p = 1.0 and pinning radius r_p = 0.35. In this case a disordered structure or skyrmion glass phase occurs. For a vortex system with strong disorder, the vortex positions are also strongly disordered and the system forms a glasslike state [2]. Further work could focus on whether there is a well defined transition to a disordered state as function of disorder strength or temperature.

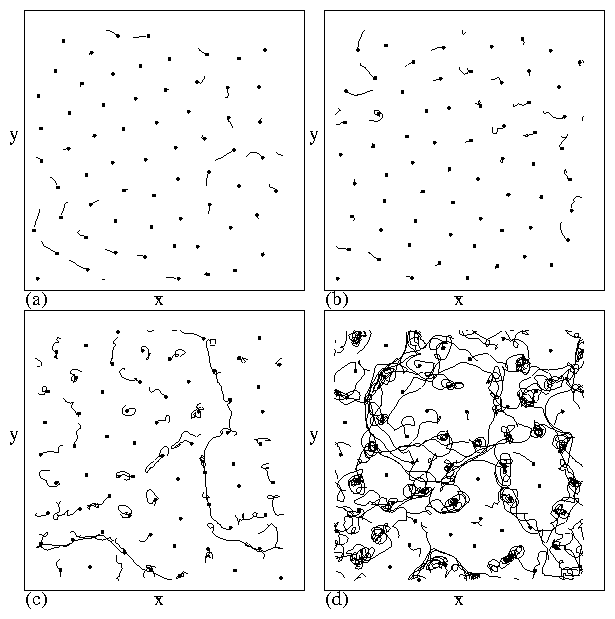Figure 2: The locations (black dots) and trajectories (black lines) of the skyrmions in a system with N_s = 64 and N_p = 51 after a rapid thermal quench. The trajectories are obtained during a fixed period of time after the quench. (a) β/α = 0.0. (b) β/α = 1.73. (c) β/α = 10. (d) β/α = 40. As the Magnus term β increases, there is more motion after the quench with increasingly circular features. This is consistent with previous work showing that increasing the Magnus term lowers the effectiveness of the pinning.

The role played by the Magnus term when the skyrmions are moving is revealed by conducting a thermal quench. Here, we start the system in a higher temperature state and rapidly cool to T = 0 in order to put the system into a strongly nonequilibrium state. The particles undergo transient motion as they adjust and try to lower their positional energy. Here we consider a system with N_s = 64, N_p = 51, and F_p = 0.25, and measure the particle trajectories over a fixed period of time after the quench. In Fig. 2(a) we show a system with β/α = 0 which is the superconducting vortex case. Here, a large number of particles are immediately immobilized by pinning sites, and there are small patches of transient motion where the particles move in almost straight paths. In this damping-dominated regime, the motion quickly disappears. In Fig. 2(b) at β/α = 1.73, there are still a number of pinned particles; however, the trajectories of the moving particles are more circular. For β/α = 10.0 in Fig. 2(c), there are a larger number of particles in motion and the circular nature of the trajectories is more prominent. The increased motion indicates that the particles effectively experience a lower pinning force due to the Magnus term, which has a tendency to cause particles to move perpendicular to an attractive force such as the pinning sites. This phenomenon was also observed in continuum simulations and was argued to be the reason that pinning is weak in skyrmion systems [39,41]. The system eventually settles into a motion free state after some time, and this transient time increases with increasing β/α. In Fig. 2(d), at β/α = 40 the circular motion is much stronger and there are even fewer stationary particles.

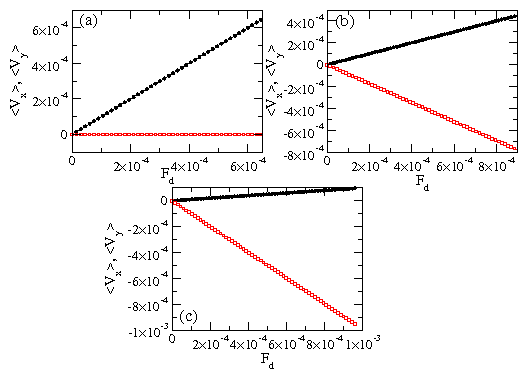Figure 3: The average velocity per particle vs external drive F_d for a skyrmion system in the absence of quenched disorder. Filled circles (upper curves): 〈V_x〉; open squares (lower curves): 〈V_y〉. (a) β/α = 0.0, where 〈V_x〉 is finite and 〈V_y〉 = 0. (b) β/α = 3.87, where the skyrmions move in both the y and x-directions. (c) β/α = 10, where the motion is predominantly in the y-direction.

4. Transport

We next consider the transport for skyrmion systems in the absence of disorder. We apply a uniform Lorentz force of magnitude F_d along the positive x direction to all the particles and measure the average velocity per particle vs F_d. In Fig. 3(a) we plot 〈V_x〉 and 〈V_y〉 versus F_d for β/α = 0. In this case, the skyrmions form a lattice that moves along the x-direction with a velocity parallel to the driving direction. In Fig. 3(b), at β/α = 3.87, the skyrmions do not move strictly in the x direction but move at angle of −60^° with respect to the driving direction. The angle of motion θ obeys tan(θ)=β/α. In Fig. 3(c) at β/α = 10, the skyrmion motion is mostly in the y direction at an angle of −84^° to the driving direction. This result shows that as the Magnus term increases, the skyrmions move increasingly in the transverse direction to an applied driving force. In an experiment, the driving force originates from the Lorentz force from an applied current. This means that as the Magnus force increases, the skyrmions will move increasingly perpendicular to the Lorentz force and will come closer to moving in the direction of the applied current, in agreement with experiment [37] and simulations [39,40,41]. Future studies will focus on how the Magnus forces affects the transport curves in the presence of pinning sites.

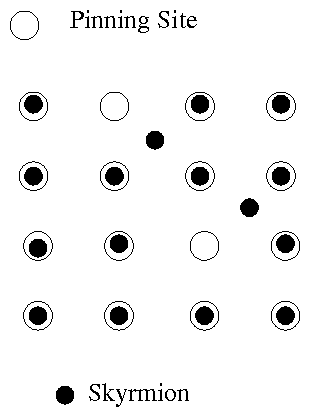Figure 4: Schematic of skyrmions interacting with a periodic pinning array. Here it may be possible to stabilize a skyrmion lattice with square symmetry and to observe different types of commensuration effects similar to those found in vortex systems with periodic pinning arrays.

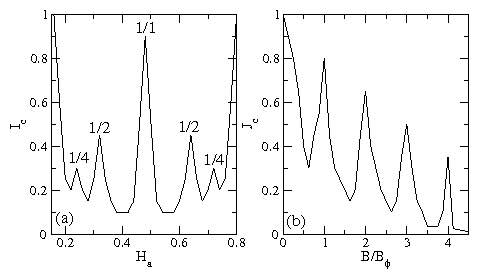Figure 5: (a) Schematic of possible critical current behavior vs applied field H_a for a skyrmion system in a square periodic pinning array. In the skyrmion system, the density of skyrmions passes through a maximum at intermediate fields (shown in the schematic as H_a=0.5). If the square periodic pinning arrays has a one-to-one matching with the maximum skyrmion density, then a peak in the critical current could occur at the one-to-one matching field, with smaller peaks for 1/2 and 1/4 matching. The 1/2 and 1/4 matchings would occur twice. (b) A schematic of the behavior of the critical current J_c of superconducting vortices interacting with a square periodic pinning array as a function of the applied magnetic field B/B_ϕ, where B_ϕ is the matching field. Here, there are peaks at the integer matching fields; however, the critical current generally decreases as the number of vortices increases.

5. Discussion

It would be very interacting to explore how skyrmions would interact with artificial pinning arrays. One of the most basic questions is what types of commensuration effects would occur when the number of skyrmions is an integer multiple of the number of pinning sites. It may also be possible to stabilize new types of skyrmion lattice structures with square or other symmetries. In Fig. 4 we show a schematic of skyrmions interacting with a square periodic pinning array. In the schematic it is assumed that the skyrmions are attracted to the pinning sites; however, it should be possible to create anti-pinning sites or areas that repel the skyrmions by suitably modifying the exchange energy on a local scale. In the case of superconducting vortices, a common method for creating artificial pinning sites is to use nanohole arrays [4,5]. It is not known if a skyrmion would be pinned by a nanohole or if it can even exist inside a nanohole. It should also be possible to create blind holes or regions where the sample is thinner or thicker than average, although the effects of such regions on skyrmions is unclear. In vortex systems, the magnetic flux is real and is conserved; however, for skyrmion systems, the flux carried by a skyrmion is artificial and thus is not necessarily conserved, so it is possible that thickness modulations would simply produce different local skyrmion densities. It is also possible that the size or shape of the skyrmion could be modified by a pinning site.

If commensuration effects occur in skyrmion systems as a function of applied field, they would differ from those found for superconducting vortices since the skyrmion number is a non-monotonic function of the applied magnetic field [35]. As the field is increased from a low value, the skyrmion number starts out small and increases until reaching a maximum for an intermediate field value. As the magnetic field is further increased, the skyrmion number decreases again before reaching zero when the system enters a ferromagnetic state. If a periodic pinning array were added to the sample such that the number of pinning sites matches the peak number of skyrmions present, then the critical current as a function of applied field H_a could have the form shown schematically in Fig. 5(a). The critical current is initially high for low skyrmion densities, and passes through a commensurate peak at intermediate fields where there is a one-to-one matching of the skyrmions to the pinning sites. It is also possible that commensurate effects would arise at rational fractional fillings such as 1/2 and 1/4, and due to the nonmonotonic dependence of skyrmion density on field, these matchings would occur twice as a function of increasing field as shown in the schematic. In Fig. 5(b) this is contrasted with the critical current behavior for vortices in superconductors with periodic pinning sites, where integer matching peaks appear at B/B_ϕ = n, where n is an integer and B_ϕ is the matching field. In the vortex system, the magnitude of the critical current generally decreases with increasing B; in the skyrmion system, the critical current might be highest when the density of skyrmions is lowest, which occurs at both low and high values of magnetic field. It may also be possible to create asymmetric pinning geometries in order to realize skyrmion ratchets or diodes, similar to the ratchet effects observed in vortex systems with asymmetric pinning [27,28,29,30]. There is already some theoretical work showing how the Magnus term can lead to rectification effects [44].

There is also the possibility that skyrmions could exhibit a melting transition for increasing temperature. In superconductors, there is a phenomenon known as the peak effect that occurs as function of field or temperature which has been associated with a softening of the vortex lattice that allows the vortices to adjust their positions and become better pinned [8]. It would be interesting to see if a similar peak effect phenomenon could occur in skyrmion systems as the temperature is raised. Skyrmions are also expected to have tube like structures in 3D, so a transformer geometry could be constructed where the top portion of the sample is driven while the response in the bottom portion of the sample is measured. In this way it could be possible to observe cutting phenomena or entanglement effects or to measure the skyrmion line tension.

One difficulty with the experimental study of skyrmion motion compared to vortex systems is that for the vortex system, the motion is tied to the onset of dissipation. The skyrmion samples are not superconducting, so if a current is applied, the motion of the skyrmions can be masked by a strong background dissipation signal, which must be separated from the transport signal generated by the skyrmions. This separation has already been achieved in experiment; however, the skyrmion signal can be small [36]. Another possibility would be to use imaging techniques and directly measure the skyrmion motion, such as by using Lorentz microscopy [37].

6. Summary

In summary, we have compared the particle based model of vortices in type-II superconductors to that of skyrmions in chiral magnets. The equations of motion for the two systems are similar; however, for the skyrmion systems the Magnus term is important and can be the dominant term influencing the dynamics of the skyrmion. We show that in this model the skyrmions form a triangular lattice in the absence of pinning and a disordered state in the presence of strong pinning. The role of the Magnus force can be more clearly observed by conducting quenched simulations and observing the transient particle motion in the presence of pinning. In the case where the Magnus term is dominant, the particles show a long time transient motion and are weakly pinned. Under an applied drive, the skyrmions move increasingly in the direction transverse to the drive as the contribution of the Magnus term is increased. We also discuss how many of the ideas for pinning and dynamics of vortices could be applied to skyrmion systems, such as creating periodic pinning arrays, ratchet geometries, or transformer geometries, or looking for peak effect type phenomena.

Acknowledgment

This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396.

References

[1]: M. Tinkham, Introduction to Superconductivity (McGraw-Hill, New York, 1975).
[2]: G. Blatter, M.V. Feigelman, V.B. Geshkenbein, A.I. Larkin, V.M. Vinokur, Rev. Mod. Phys. 66 (1994) 1125.
[3]: L. Civale, A.D. Marwick, T.K. Worthington, M.A. Kirk, J.R. Thompson, L. Krusin-Elbaum, Y. Sun, J.R. Clem, F. Holtzberg, Phys. Rev. Lett. 67 (1991) 648.
[4]: M. Baert, V.V. Metlushko, R. Jonckheere, V.V. Moshchalkov, Y. Bruynseraede, Phys. Rev. Lett. 74 (1995) 3269; Europhys. Lett. 29 (1995) 157.
[5]: K. Harada, O. Kamimura, H. Kasai, T. Matsuda, A. Tonomura, V.V. Moshchalkov, Science 274 (1996) 1167.
[6]: U. Welp, Z.L. Xiao, J.S. Jiang, V.K. Vlasko-Vlasov, S.D. Bader, G.W. Crabtree, J. Liang, H. Chik, J.M. Xu, Phys. Rev. B 66 (2002) 212507.
[7]: C. Reichhardt, C.J. Olson Reichhardt, Phys. Rev. Lett. 103 (2009) 168301; S. Okuma, Y. Tsugawa, A. Motohashi, Phys. Rev. B 83 (2011) 012503.
[8]: S. Bhattacharya, M. J. Higgins, Phys. Rev. Lett. 70 (1993) 2617.
[9]: A.E. Koshelev, V.M. Vinokur, Phys. Rev. Lett. 73 (1994) 3580.
[10]: C.J. Olson, C. Reichhardt, F. Nori, Phys. Rev. Lett. 81 (1998) 3757.
[11]: F. Pardo, F. de la Cruz, P.L. Gammel, E. Bucher, D.J. Bishop, Nature (London) 396 (1998) 348.
[12]: C.J. Olson, C. Reichhardt, R.T. Scalettar, G.T. Zimányi, N. Gr onbech-Jensen, Phys. Rev. B 67 (2003) 184523.
[13]: M. Pleimling, U.C. Täuber, Phys. Rev. B 84 (2011) 174509.
[14]: J.I. Martín, M. Vélez, J. Nogués, I.K. Schuller, Phys. Rev. Lett. 79 (1997) 1929; M.J. Van Bael, K. Temst, V.V. Moshchalkov, Y. Bruynseraede, Phys. Rev. B 59 (1999) 14674.
[15]: C. Reichhardt, G.T. Zimányi, R.T. Scalettar, A. Hoffmann, I.K. Schuller, Phys. Rev. B 64 (2001) 052503; C. Reichhardt, N. Gr onbech-Jensen, Phys. Rev. B 63 (2001) 054510; C. Reichhardt, C.J. Olson, R.T. Scalettar, G.T. Zimányi, Phys. Rev. B 64 (2001) 144509.
[16]: A.N. Grigorenko, S.J. Bending, M.J. Van Bael, M. Lange, V.V. Moshchalkov, H. Fangohr, and P.A. de Groot, Phys. Rev. Lett. 90 (2003) 237001.
[17]: G. Karapetrov, J. Fedor, M. Iavarone, D. Rosenmann, W.K. Kwok, Phys. Rev. Lett. 95 (2005) 167002.
[18]: G.R. Berdiyorov, M.V. Milosevic, F.M. Peeters, Europhys. Lett. 74 (2006) 493; Phys. Rev. B 74 (2006) 174512.
[19]: C.J. Olson Reichhardt, A. Libál, C. Reichhardt, Phys. Rev. B 73 (2006) 184519.
[20]: W.J. Zhang, S.K. He, H.F. Liu, G.M. Xue, H. Xiao, B.H. Li, Z.C. Wen, X.F. Han, S.P. Zhao, C.Z. Gu, X.G. Qiu, V.V. Moshchalkov, EPL 99 (2012) 37006.
[21]: I. Swiecicki, C. Ulysse, T. Wolf, R. Bernard, N. Bergeal, J. Briatico, G. Faini, J. Lesueur, J.E. Villegas, Phys. Rev. B 85 (2012) 224502.
[22]: C. Reichhardt, N. Gronbech-Jensen, Phys. Rev. B 63 (2001) 054510.
[23]: C. Reichhardt, C.J. Olson, F. Nori, Phys. Rev. Lett. 78 (1997) 2648.
[24]: C. Reichhardt, C.J. Olson Reichhardt, Phys. Rev. B 78 (2008) 224511.
[25]: J. Gutierrez, A.V. Silhanek, J. Van de Vondel, W. Gillijns, V.V. Moshchalkov, Phys. Rev. B 80 (2009) 140514; S. Avci, Z.L. Xiao, J. Hua, A. Imre, R. Divan, J. Pearson, U. Welp, W.K. Kwok, G.W. Crabtree, Appl. Phys. Lett. 97 (2010) 042511.
[26]: R.M. da Silva, C.C. de Souza Silva, Phys. Rev. B 83 (2011) 184514.
[27]: C.S. Lee, B. Jankó, I. Derényi, A.L. Barabási, Nature (London) 400 (1999) 337.
[28]: J. Van de Vondel, C.C. de Souza Silva, B.Y. Zhu, M. Morelle, V.V. Moshchalkov, Phys. Rev. Lett. 94 (2005) 057003.
[29]: Q. Lu, C.J. Olson Reichhardt, C. Reichhardt, Phys. Rev. B 75 (2007) 054502. W. Gillijns, A.V. Silhanek, V.V. Moshchalkov, C.J. Olson Reichhardt, C. Reichhardt, Phys. Rev. Lett. 99 (2007) 247002.
[30]: N.S. Lin, T.W. Heitmann, K. Yu, B.L.T. Plourde, V.R. Misko, Phys. Rev. B 84 (2011) 144511; G. Karapetrov, V. Yefremenko, G. Mihajlovic, J.E. Pearson, M. Iavarone, V. Novosad, S.D. Bader, Phys. Rev. B 86 (2012) 054524.
[31]: M.B. Hastings, C.J. Olson Reichhardt, C. Reichhardt, Phys. Rev. Lett. 90 (2003) 247004; M.V. Milosevic, G.R. Berdiyorov, F.M. Peeters, Appl. Phys. Lett. 91 (2007) 212501.
[32]: T.H.R. Skyrme, Proc. R. Soc. London, Ser. A 260 (1961) 127.
[33]: A. Bogdanov and A. Hubert, J. Magn. Magn. Mater. 138 (1994) 255; U.K. Rössler, A.N. Bogdanov, C. Pfleiderer, Nature (London) 442 (2006) 797.
[34]: S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii, P. Böni, Science 323 (2009) 915.
[35]: X.Z. Yu, Y. Onose, N. Kanazawa, J.H. Park, J.H. Han, Y. Matsui, N. Nagaosa, Y. Tokura, Nature (London) 465 (2010) 901; X.Z. Yu, N. Kanazawa, Y. Onose, K. Kimoto, W.Z. Zhang, S. Ishiwata, Y. Matsui, Y. Tokura, Nature Mater. 10 (2011) 106 (2011); S. Seki, X.Z. Yu, S. Ishiwata, Y. Tokura, Science 336 (2012) 198.
[36]: T. Schulz, R. Ritz, A. Bauer, M. Halder, M. Wagner, C. Franz, C. Pfleiderer, K. Everschor, M. Garst, A. Rosch, Nat. Phys. 8 (2012) 301.
[37]: X.Z. Yu, N. Kanazawa, W.Z. Zhang, T. Nagai, T. Hara, K. Kimoto, Y. Matsui, Y. Onose, Y. Tokura, Nat. Commun. 3 (2012) 988.
[38]: N. Nagaosa, Y. Tokura, Nat. Nanotechnol. 8 (2013) 899.
[39]: J. Iwasaki, M. Mochizuki, N. Nagaosa, Nat. Commun. 4 (2013) 1463.
[40]: S.Z. Lin, C. Reichhardt, C.D. Batista, A. Saxena, Phys. Rev. Lett. 110 (2013) 207202.
[41]: S.-Z. Lin, C. Reichhardt, C.D. Batista, A. Saxena, Phys. Rev. B 87 (2013) 214419.
[42]: C. Reichhardt, C.J. Olson, J. Groth, S. Field, F. Nori, Phys. Rev. B 52 (1995) 10441; J. Groth, C. Reichhardt, C.J. Olson, S.B. Field, F. Nori, Phys. Rev. Lett. 77 (1996) 3625; D. Ray, C.J. Olson Reichhardt, B. Jankó, C. Reichhardt, Phys. Rev. Lett. 110 (2013) 267001.
[43]: A.A. Thiele, Phys. Rev. Lett. 30 (1973) 230.
[44]: S.-Z. Lin, C. Reichhardt, A. Saxena, Appl. Phys. Lett. 102 (2013) 222405.

File translated from T_EX by T_THgold, version 4.00.
Back to Home