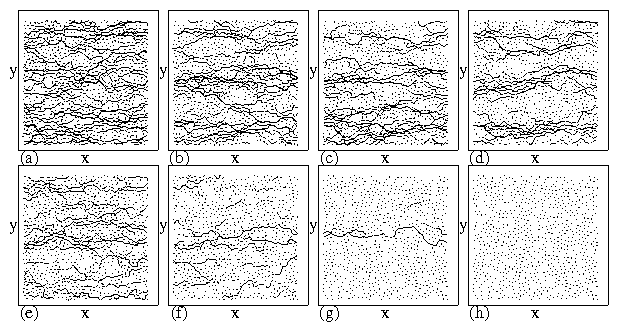
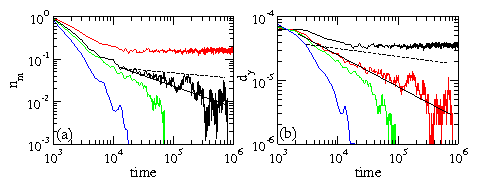
 Figure 4:
The L=48 system from Fig. 2(b). (a) nm, the fraction of
moving particles, versus time for Fp/Fpc=0.927, 1.008, 1.05, and 1.2
(from top to bottom). Straight line: a power law fit with α = 1/2.
Dashed line: a power law fit with α = 0.125.
(b) dy, the displacements in the y directions, versus time for
Fp/Fpc=0.927, 1.008, 1.05, and 1.2 (from top to bottom). Straight
line: a power law fit with α = 1/2. Dashed line: a power law fit
with α = 0.125.
Figure 4:
The L=48 system from Fig. 2(b). (a) nm, the fraction of
moving particles, versus time for Fp/Fpc=0.927, 1.008, 1.05, and 1.2
(from top to bottom). Straight line: a power law fit with α = 1/2.
Dashed line: a power law fit with α = 0.125.
(b) dy, the displacements in the y directions, versus time for
Fp/Fpc=0.927, 1.008, 1.05, and 1.2 (from top to bottom). Straight
line: a power law fit with α = 1/2. Dashed line: a power law fit
with α = 0.125.
|