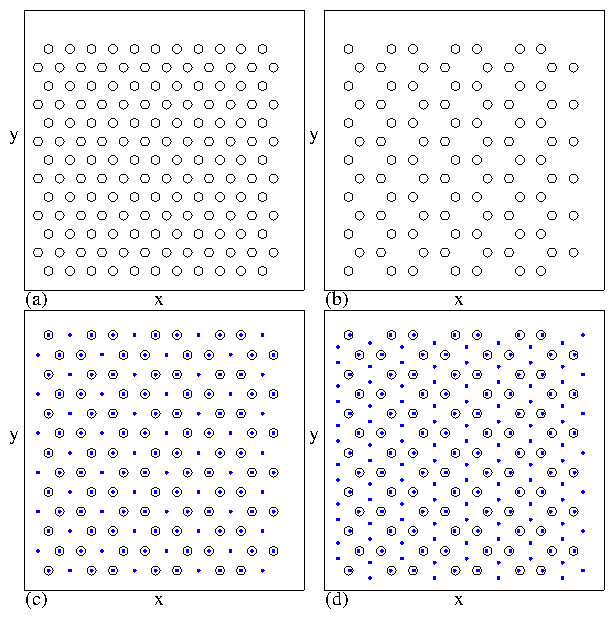
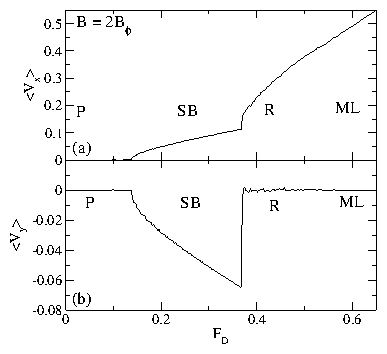
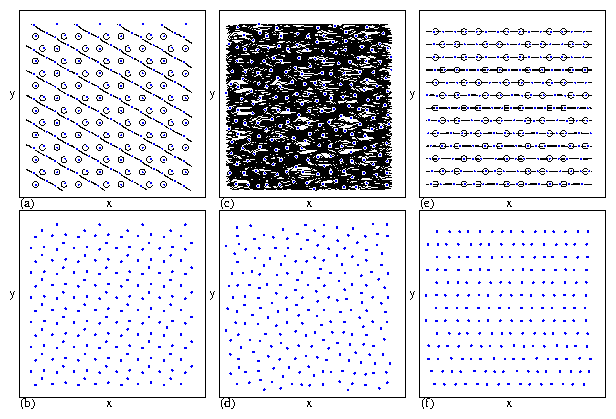
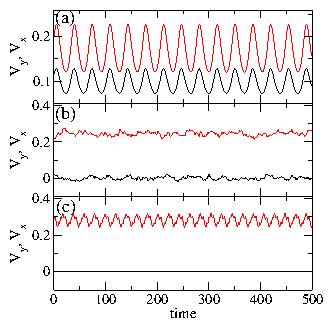
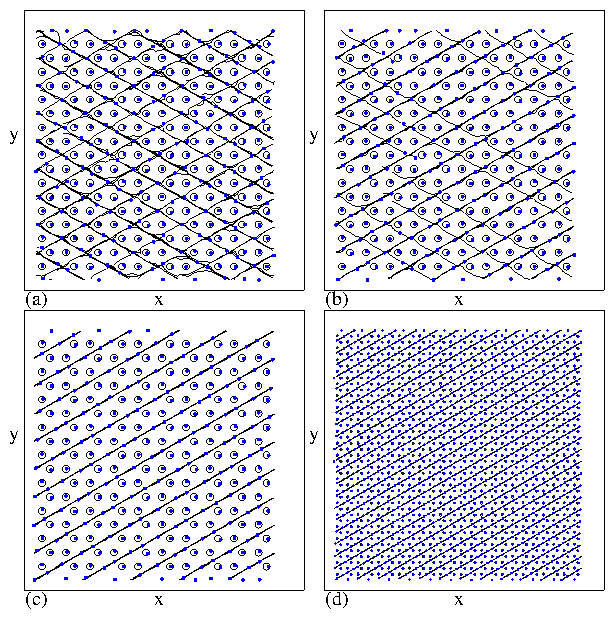
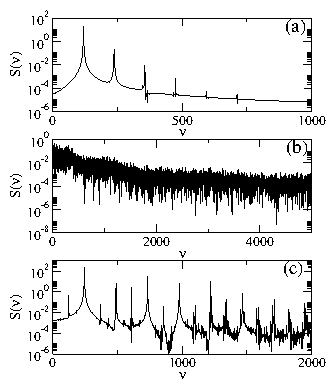
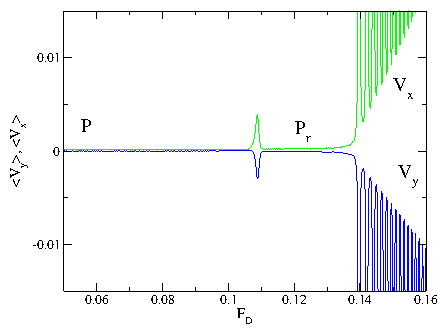
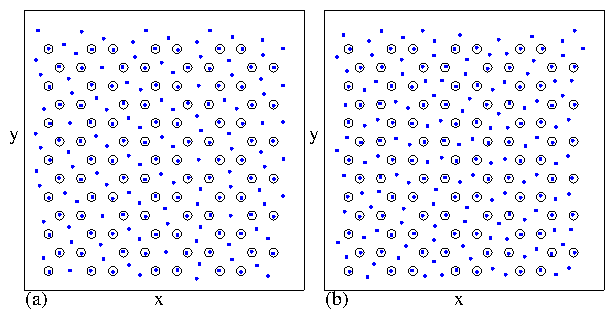
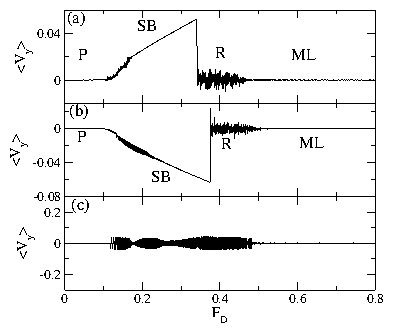
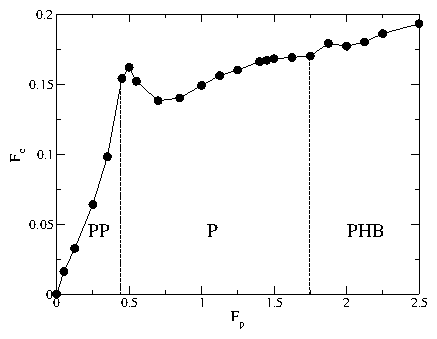
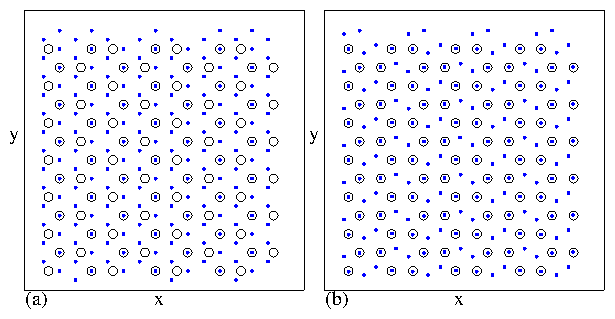
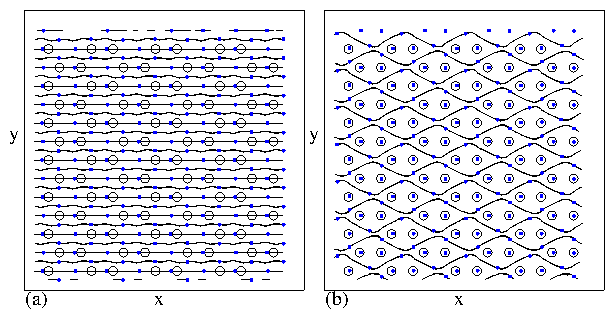
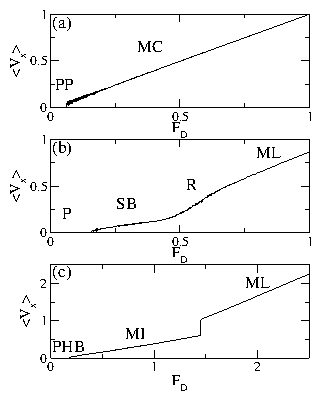
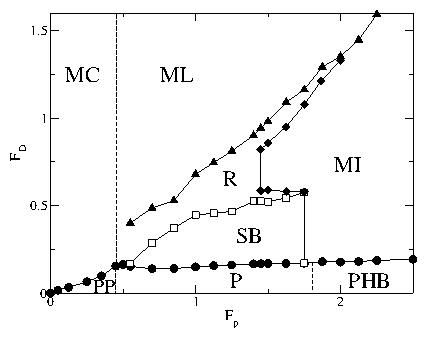
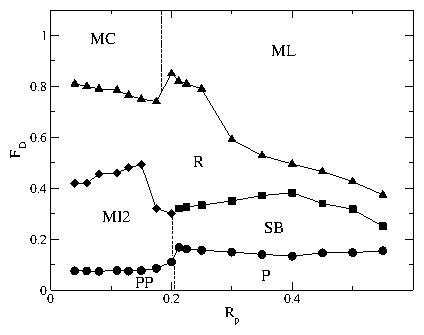
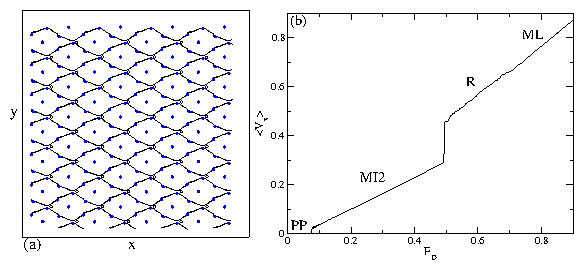
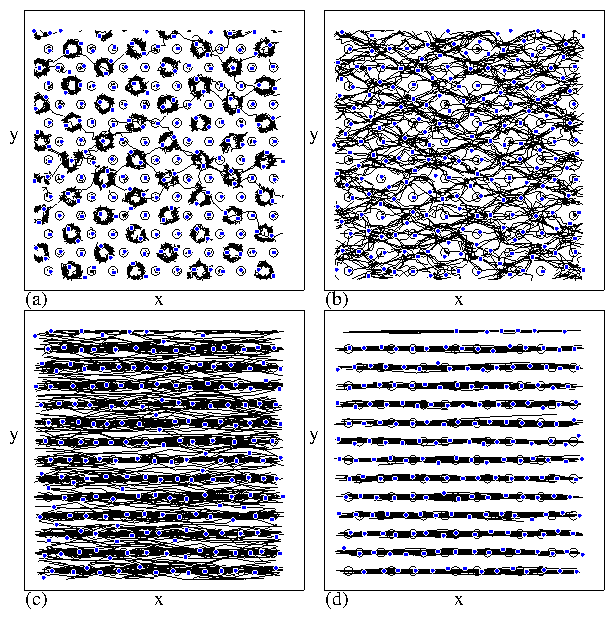
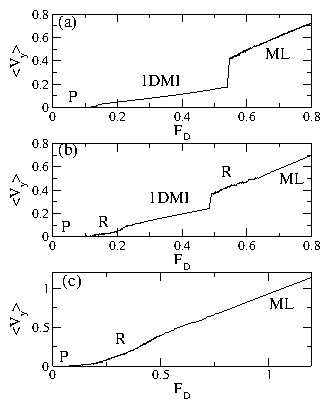
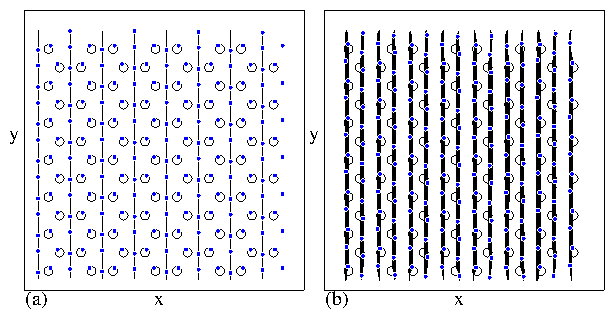
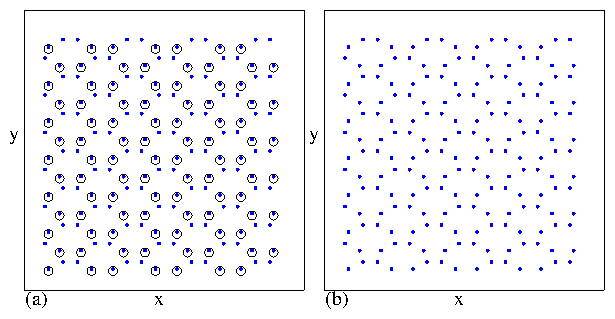
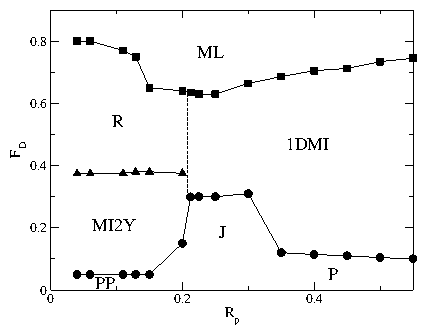
 Figure 29:
The critical depinning force in the x-direction, Fxc
(open squares),
and in the y-direction, Fyc (filled circles), vs Fp
for B/Bϕ = 2.0, Rp = 0.35λ,
and np=0.3125/λ2.
PP: partially pinned phase; P: pinned dimer phase; PHB: pinned herringbone
phase; J: jammed state.
In the PP phase, Fcx=Fcy, while in the P phase, Fcx > Fcy.
A large enhancement of Fcy occurs in the PHB phase when dimer jamming
occurs.
Inset: the ratio Fyc/Fxc vs Fp. The dashed line
indicates Fyc/Fxc=1, where
the depinning thresholds are equal.
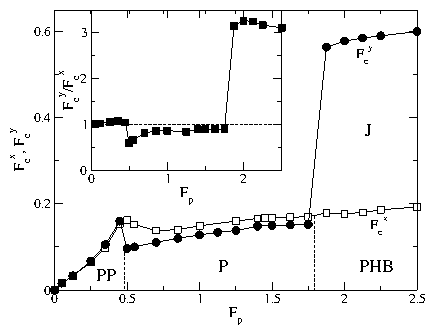
Figure 29:
The critical depinning force in the x-direction, Fxc
(open squares),
and in the y-direction, Fyc (filled circles), vs Fp
for B/Bϕ = 2.0, Rp = 0.35λ,
and np=0.3125/λ2.
PP: partially pinned phase; P: pinned dimer phase; PHB: pinned herringbone
phase; J: jammed state.
In the PP phase, Fcx=Fcy, while in the P phase, Fcx > Fcy.
A large enhancement of Fcy occurs in the PHB phase when dimer jamming
occurs.
Inset: the ratio Fyc/Fxc vs Fp. The dashed line
indicates Fyc/Fxc=1, where
the depinning thresholds are equal.
|