ABSTRACT
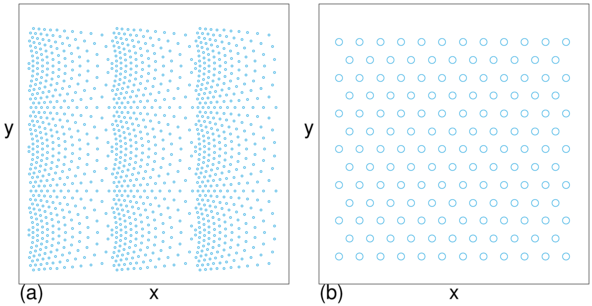
A conformal pinning array can be created by conformally transforming
a uniform triangular pinning lattice to
produces a new structure in which the six-fold ordering
of the original lattice is conserved
but where there is a spatial gradient in the density of pinning sites.
Here we examine
several aspects of vortices interacting with conformal pinning arrays and
how they can be used to create a flux flow diode effect for driving vortices in
different directions across the
arrays.
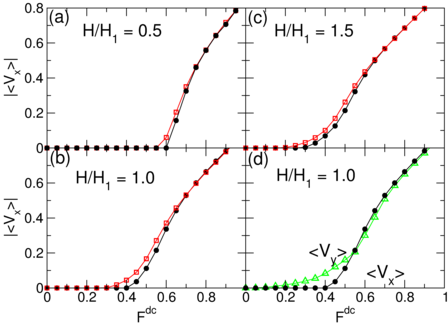
Under the application of an ac drive, a pronounced vortex ratchet effect occurs
where the vortices flow in the easy direction of the array asymmetry.
When the ac drive is applied perpendicular to the asymmetry direction of the
array, it is possible to realize a transverse vortex ratchet effect
where there is a generation of a dc flow of vortices perpendicular to the ac drive
due to the creation of a noise correlation ratchet by the plastic motion of the vortices.
We also examine vortex transport simulations in experiments and compare the pinning
effectiveness
of conformal arrays to uniform triangular pinning
arrays.
We find that a triangular array generally pins the vortices more effectively
at the first matching field and below,
while the conformal array is more effective at higher fields where
interstitial vortex flow occurs.
| (1) |
|