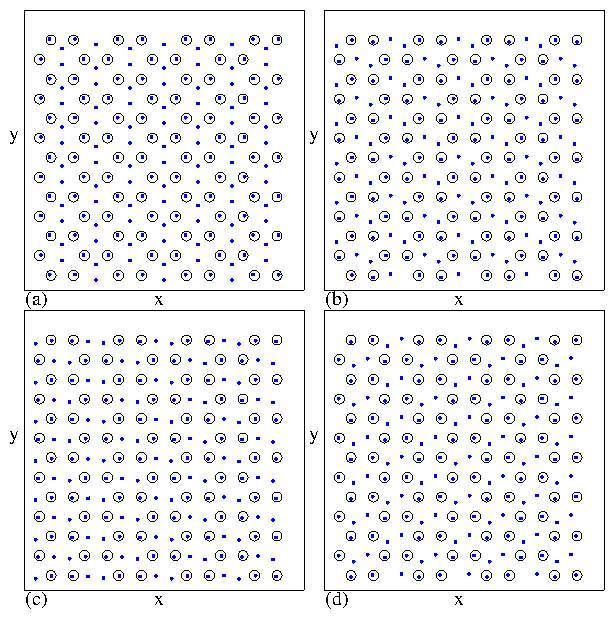
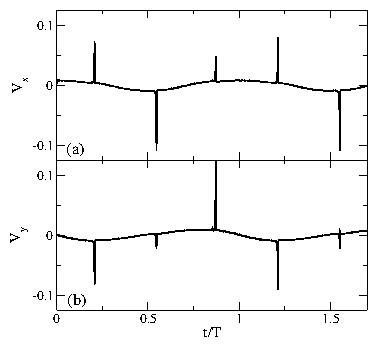
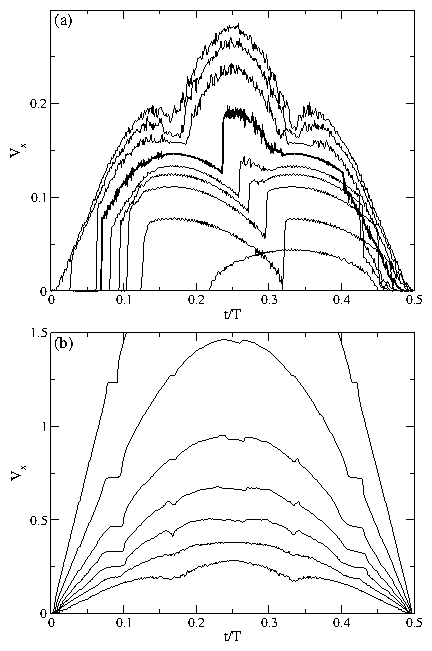
 Figure 17:
Vx versus time
for different values of the ac amplitude showing the transitions from the
random phases to the high ac drive phases.
(a) From bottom to top, A = 0.16, 0.225, 0.3, 0.325, 0.33, 0.35, 0.38, 0.405,
and 0.43.
The A=0.35 curve is highlighed with a darker line.
(b) From bottom to top, A = 0.43, 0.5, 0.6, 0.75, 1.0, 1.5, and 2.5.
Figure 17:
Vx versus time
for different values of the ac amplitude showing the transitions from the
random phases to the high ac drive phases.
(a) From bottom to top, A = 0.16, 0.225, 0.3, 0.325, 0.33, 0.35, 0.38, 0.405,
and 0.43.
The A=0.35 curve is highlighed with a darker line.
(b) From bottom to top, A = 0.43, 0.5, 0.6, 0.75, 1.0, 1.5, and 2.5.
|