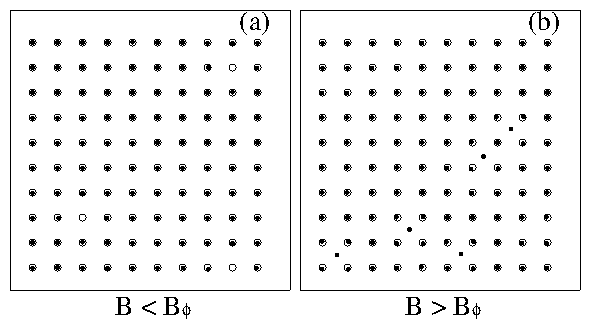
 Figure 4:
Snapshots (left panels) and trajectories (right panels) of vortices
for regions IV (1D incommensurate flow)
and V (incomm. and commensurate plastic flow) of Fig. 2(a).
In (a,b) we can see that the vortex lattice structure and flow
patterns are quite different from those shown in Fig. 3.
In (a) vortices are now aligned with the
pinning rows, with certain rows forming 1D incommensurate
structures. In (b) it can be seen that the motion
in region IV is 1D,
but unlike the interstitial flow in phase II, where the
vortices flowed between the
pinning rows, the vortices now
flow along the pinning rows.
Rows containing an incommensurate
number of vortices (i.e., where there are
more vortices than pinning sites)
are the only places where
motion is occurring, while rows with a commensurate number of vortices
remain pinned.
In particular, note that the first, second, fourth, seventh, and ninth
(commensurate)
rows from the top edge
remain pinned while the remaining incommensurate rows slide
past the commensurate ones.
Flux motion in phase IV, shown in (b), occurs through mobile
vortex discommensurations. These "flux-solitons" propagate at a
faster speed than the actual vortices.
In (c,d) the entire
vortex lattice is moving
in 1D paths along the pinning rows, corresponding to phase V.
The vortex lattice in (c) is not
triangular,
but is similar to that seen in phase IV.
The defects caused by the incommensurate vortices
(discommensurations or flux solitons)
do not heal out
since vortex motion in the transverse direction does not occur
in regions IV and V.
The incommensurate rows are more mobile than the commensurate rows
so they slip past the commensurate rows; thus the vortex motion is
always plastic.
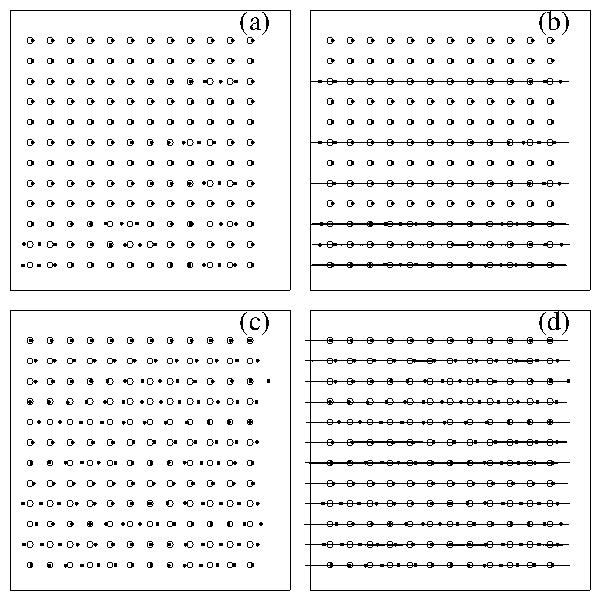
Figure 4:
Snapshots (left panels) and trajectories (right panels) of vortices
for regions IV (1D incommensurate flow)
and V (incomm. and commensurate plastic flow) of Fig. 2(a).
In (a,b) we can see that the vortex lattice structure and flow
patterns are quite different from those shown in Fig. 3.
In (a) vortices are now aligned with the
pinning rows, with certain rows forming 1D incommensurate
structures. In (b) it can be seen that the motion
in region IV is 1D,
but unlike the interstitial flow in phase II, where the
vortices flowed between the
pinning rows, the vortices now
flow along the pinning rows.
Rows containing an incommensurate
number of vortices (i.e., where there are
more vortices than pinning sites)
are the only places where
motion is occurring, while rows with a commensurate number of vortices
remain pinned.
In particular, note that the first, second, fourth, seventh, and ninth
(commensurate)
rows from the top edge
remain pinned while the remaining incommensurate rows slide
past the commensurate ones.
Flux motion in phase IV, shown in (b), occurs through mobile
vortex discommensurations. These "flux-solitons" propagate at a
faster speed than the actual vortices.
In (c,d) the entire
vortex lattice is moving
in 1D paths along the pinning rows, corresponding to phase V.
The vortex lattice in (c) is not
triangular,
but is similar to that seen in phase IV.
The defects caused by the incommensurate vortices
(discommensurations or flux solitons)
do not heal out
since vortex motion in the transverse direction does not occur
in regions IV and V.
The incommensurate rows are more mobile than the commensurate rows
so they slip past the commensurate rows; thus the vortex motion is
always plastic.
|