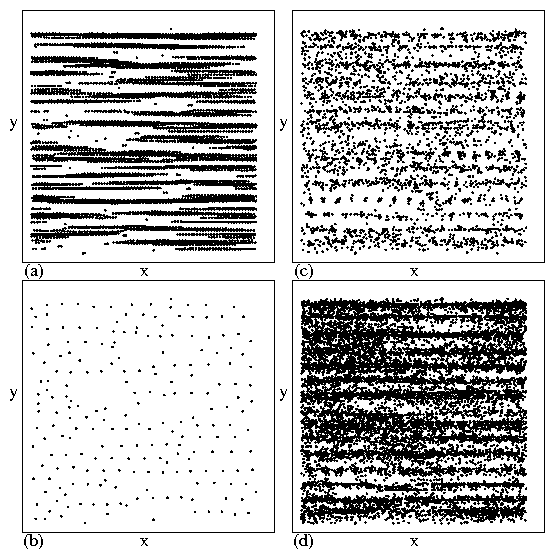
 Figure 1:
Black dots: Stroboscopic vortex positions marked every 0.01τ in
(a) and every τ in (b),(c),(d).
(a) Vortex positions
during n=4 cycles in
a sample with nv = 0.052/λ2
and d=48λ.
(b) Vortex positions
in the same sample as (a).
In this reversible regime, all of the vortices return to their
initial positions after each cycle.
(c) Positions in a sample with a longer
d=160λ
in n=25 cycles. The vortices do not return to their initial
positions and the behavior is irreversible.
(d) The same sample as (c) for n=100 cycles
showing that the displacements are anisotropic.
Figure 1:
Black dots: Stroboscopic vortex positions marked every 0.01τ in
(a) and every τ in (b),(c),(d).
(a) Vortex positions
during n=4 cycles in
a sample with nv = 0.052/λ2
and d=48λ.
(b) Vortex positions
in the same sample as (a).
In this reversible regime, all of the vortices return to their
initial positions after each cycle.
(c) Positions in a sample with a longer
d=160λ
in n=25 cycles. The vortices do not return to their initial
positions and the behavior is irreversible.
(d) The same sample as (c) for n=100 cycles
showing that the displacements are anisotropic.
|
