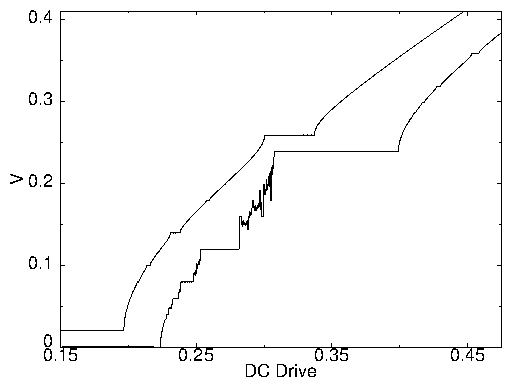
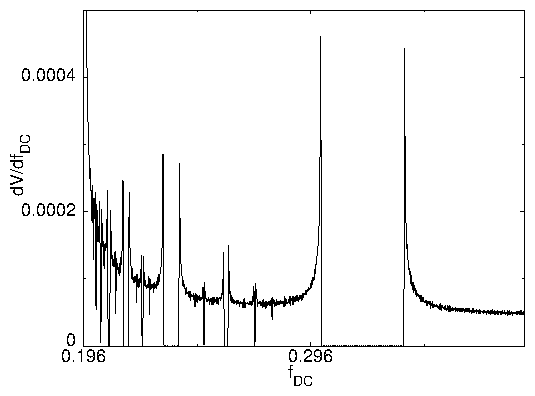
 Figure 10:
The V vs fDC curves for different temperatures for B/Bϕ = 2.0
and A = 0.35. The curves have been shifted up from zero for presentation.
From lowest to highest, T/Tm = 0.0, 0.07, 0.28, 0.64, 0.75,
0.87, and 0.96, where Tm is the melting temperature.
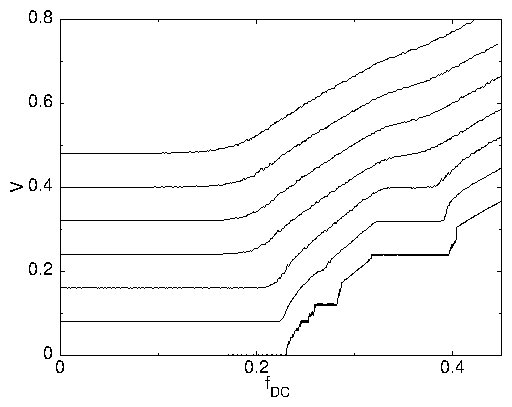
Figure 10:
The V vs fDC curves for different temperatures for B/Bϕ = 2.0
and A = 0.35. The curves have been shifted up from zero for presentation.
From lowest to highest, T/Tm = 0.0, 0.07, 0.28, 0.64, 0.75,
0.87, and 0.96, where Tm is the melting temperature.
|