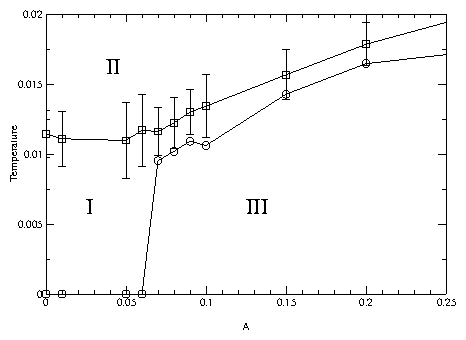
 Figure 1: The colloidal configurations for a square periodic substrate in 2D.
The circles indicate the location of the potential wells.
(a) For a sufficiently weak substrate potential, at low temperatures,
(here A=0.0, T=0.0)
the colloids form a floating triangular lattice, which has some mild
distortion (see text).
(b) At high enough temperature,
for any substrate potential,
(here A=1.0, T=0.125)
the colloids form a liquid. (c) For all but the
smallest potentials, at low temperatures,
(here A=1.0, T=0.0)
the colloids form a rotationally
ordered solid. (d) For large enough substrate potentials,
(here A=1.0, T=0.026)
an intermediate
disordered CMC phase exists between the rotationally ordered solid phase and
the liquid phase.
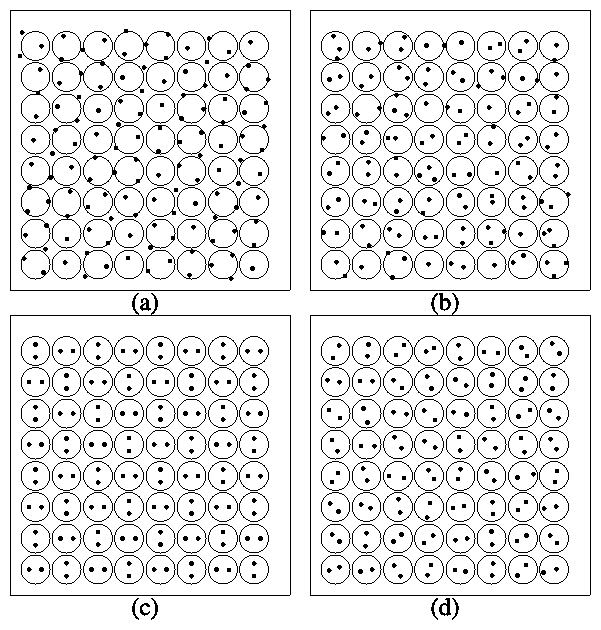
Figure 1: The colloidal configurations for a square periodic substrate in 2D.
The circles indicate the location of the potential wells.
(a) For a sufficiently weak substrate potential, at low temperatures,
(here A=0.0, T=0.0)
the colloids form a floating triangular lattice, which has some mild
distortion (see text).
(b) At high enough temperature,
for any substrate potential,
(here A=1.0, T=0.125)
the colloids form a liquid. (c) For all but the
smallest potentials, at low temperatures,
(here A=1.0, T=0.0)
the colloids form a rotationally
ordered solid. (d) For large enough substrate potentials,
(here A=1.0, T=0.026)
an intermediate
disordered CMC phase exists between the rotationally ordered solid phase and
the liquid phase.
|