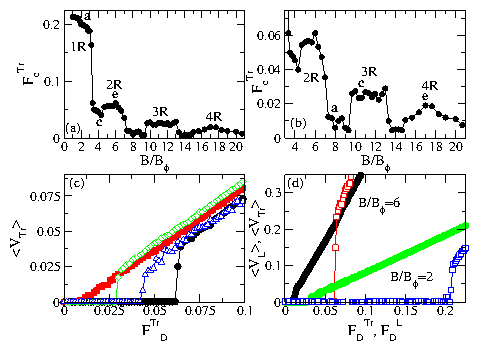
 Figure 1:
(a) The transverse critical depinning force
FTrc vs B/Bϕ for a system with
Bϕ=0.052ϕ0/λ2
and fixed
longitudinal drive
FLD = 0.6.
The points a, c, and e refer to the fields illustrated
in Fig. 2.
The maxima are labeled according to the number of moving vortex rows between
adjacent pinning rows: 1R, one row; 2R, two rows; 3R, three rows; and 4R,
four rows.
(b) A blow up of panel (a)
for B/Bϕ > 2.0.
The points a, c, and e refer to the fields illustrated
in Fig. 3.
(c) The transverse velocity 〈VTr〉 vs
transverse force FTrD for
B/Bϕ = 4.33
(open triangles),
6.0
(filled circles),
8.0
(filled squares),
and 10
(open diamonds).
(d) The scaled longitudinal velocity
〈VL〉(Nv/Np) (filled circles) versus
longitudinal drive FDL and
transverse velocity 〈VTr〉(Nv/Np) (open squares)
vs transverse drive FDTr
for B/Bϕ = 6.0 (left curves) and 2.0 (right curves).
Figure 1:
(a) The transverse critical depinning force
FTrc vs B/Bϕ for a system with
Bϕ=0.052ϕ0/λ2
and fixed
longitudinal drive
FLD = 0.6.
The points a, c, and e refer to the fields illustrated
in Fig. 2.
The maxima are labeled according to the number of moving vortex rows between
adjacent pinning rows: 1R, one row; 2R, two rows; 3R, three rows; and 4R,
four rows.
(b) A blow up of panel (a)
for B/Bϕ > 2.0.
The points a, c, and e refer to the fields illustrated
in Fig. 3.
(c) The transverse velocity 〈VTr〉 vs
transverse force FTrD for
B/Bϕ = 4.33
(open triangles),
6.0
(filled circles),
8.0
(filled squares),
and 10
(open diamonds).
(d) The scaled longitudinal velocity
〈VL〉(Nv/Np) (filled circles) versus
longitudinal drive FDL and
transverse velocity 〈VTr〉(Nv/Np) (open squares)
vs transverse drive FDTr
for B/Bϕ = 6.0 (left curves) and 2.0 (right curves).
|
