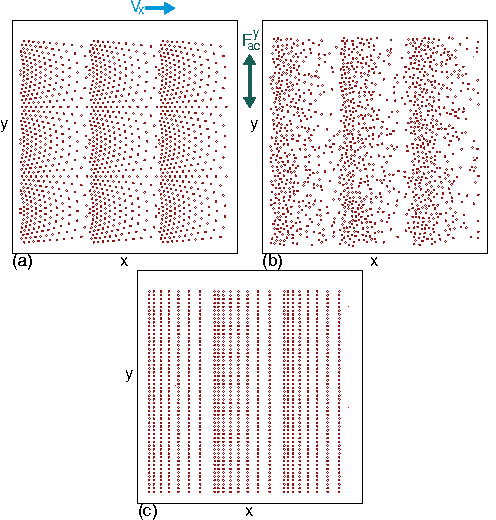
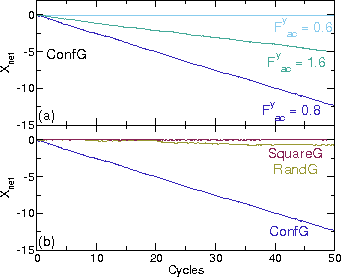
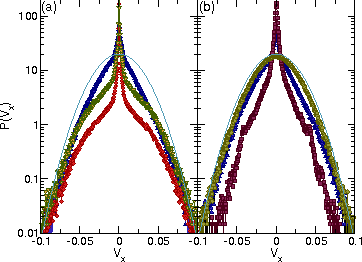
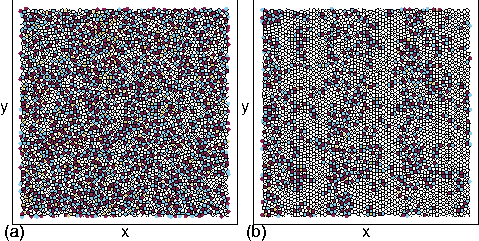
Figure 20:
(a) P(Vx) for the ConfG drift ratchet at B/Bϕ = 1.0 and Fp = 1.0 for
Fydc = 0.55 (red curve),
Fydc = 0.7 (blue curve) where the strongest transverse drift occurs, and
Fydc = 0.95 (yellow curve).
(b) P(Vx) for the ConfG (blue curve),
RandG (brown curve), and SquareG (dark red curve) drift ratchets
at B/Bϕ = 1.0, Fp = 1.0,
and Fydc = 0.7.
The smooth green line indicates a Gaussian fit.
(c)
P(|Vx|) for the ConfG drift ratchet at B/Bϕ=1.0, Fp=1.0, and
Fydc = 0.7.
The upper light blue curve is for negative Vx values, the
lower dark blue curve is for positive Vx values, and
the smooth green line is a Gaussian fit.
(d)
P(|Vx|) for the ConfG drift ratchet at B/Bϕ=1.0, Fp=1.0, and
Fydc = 0.55, where there is no net drift.
The light blue curve is for negative Vx values, the
dark blue curve is for positive Vx values, and
the smooth green line is a Gaussian fit.
There is little to no asymmetry in the velocity curves, which are both well fit
by a Gaussian distribution away from the peak near |Vx|=0.
Figure 20:
(a) P(Vx) for the ConfG drift ratchet at B/Bϕ = 1.0 and Fp = 1.0 for
Fydc = 0.55 (red curve),
Fydc = 0.7 (blue curve) where the strongest transverse drift occurs, and
Fydc = 0.95 (yellow curve).
(b) P(Vx) for the ConfG (blue curve),
RandG (brown curve), and SquareG (dark red curve) drift ratchets
at B/Bϕ = 1.0, Fp = 1.0,
and Fydc = 0.7.
The smooth green line indicates a Gaussian fit.
(c)
P(|Vx|) for the ConfG drift ratchet at B/Bϕ=1.0, Fp=1.0, and
Fydc = 0.7.
The upper light blue curve is for negative Vx values, the
lower dark blue curve is for positive Vx values, and
the smooth green line is a Gaussian fit.
(d)
P(|Vx|) for the ConfG drift ratchet at B/Bϕ=1.0, Fp=1.0, and
Fydc = 0.55, where there is no net drift.
The light blue curve is for negative Vx values, the
dark blue curve is for positive Vx values, and
the smooth green line is a Gaussian fit.
There is little to no asymmetry in the velocity curves, which are both well fit
by a Gaussian distribution away from the peak near |Vx|=0.
|