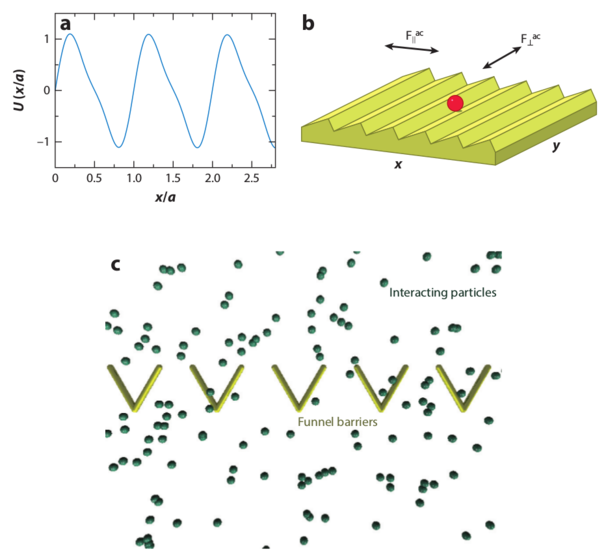
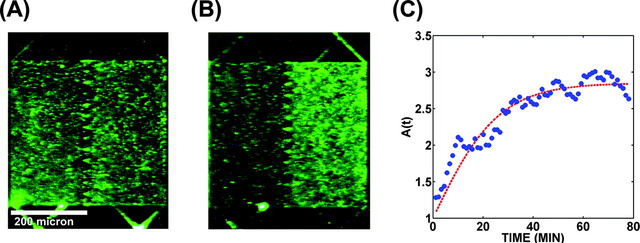
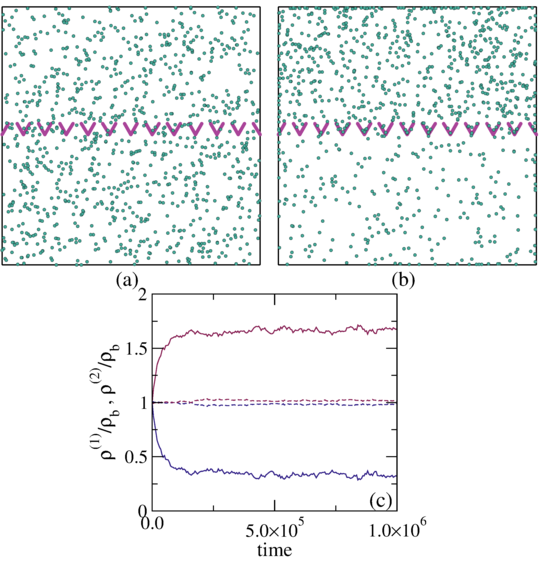
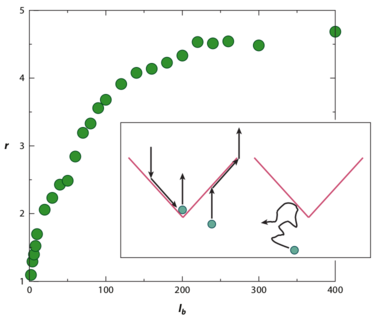
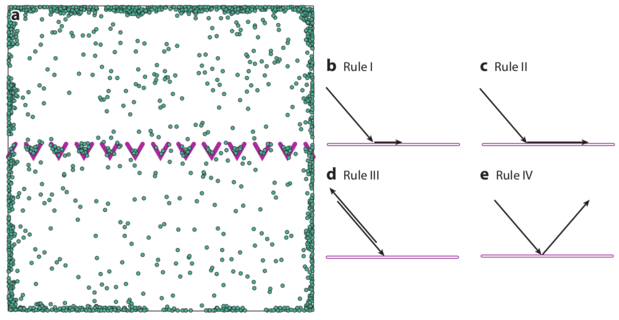
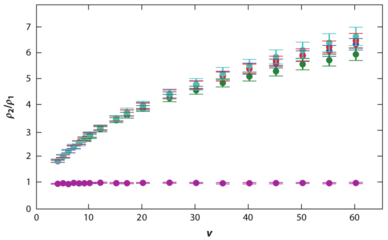
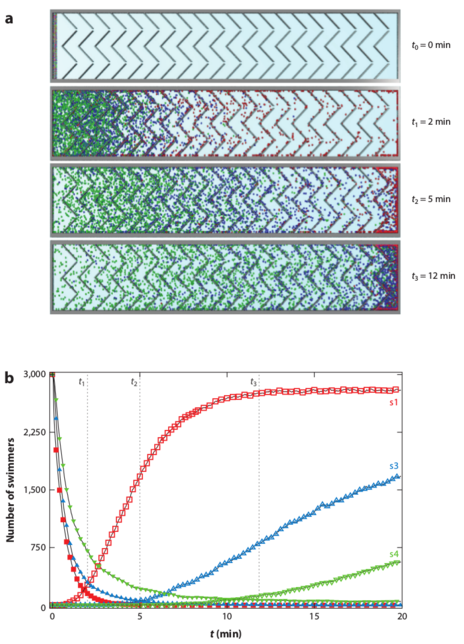
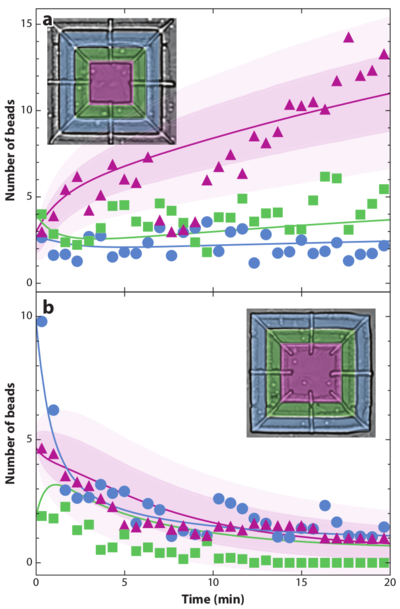
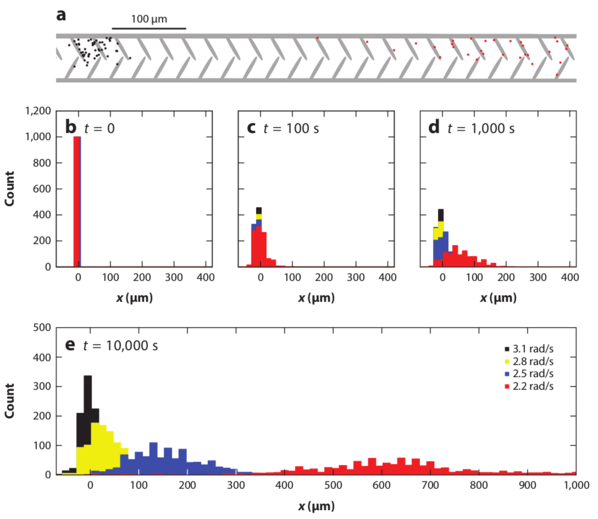
 Figure 15: Simulations of
the separation of circle swimmers with different angular velocities
by an asymmetric comb channel with the geometry illustrated in panel (a).
The particles have angular velocities of
3.1 (black), 2.8 (yellow), 2.5 (blue), and 2.2 (red) rad/sec.
(b,c,d,e) Histograms of the
particle positions for increasing times.
The particles rotating at 2.2 rad/s exhibit the largest amount of rectification.
Reproduced from
Reference 90
with permission of The Royal Society of Chemistry.
Figure 15: Simulations of
the separation of circle swimmers with different angular velocities
by an asymmetric comb channel with the geometry illustrated in panel (a).
The particles have angular velocities of
3.1 (black), 2.8 (yellow), 2.5 (blue), and 2.2 (red) rad/sec.
(b,c,d,e) Histograms of the
particle positions for increasing times.
The particles rotating at 2.2 rad/s exhibit the largest amount of rectification.
Reproduced from
Reference 90
with permission of The Royal Society of Chemistry.
|