Physical Review E 88, 062310 (2013)

Active Matter Ratchets with an External Drift

C. Reichhardt and C. J. Olson Reichhardt
Theoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA

(Received 16 August 2013; published 19 December 2013)

When active matter particles such as swimming bacteria are placed in an asymmetric array of funnels, it has been shown that a ratchet effect can occur even in the absence of an external drive. Here we examine active ratchets for two dimensional arrays of funnels or L-shapes where there is also an externally applied dc drive or drift. We show that for certain conditions, the ratchet effect can be strongly enhanced, and that it is possible to have conditions under which run-and-tumble particles with one run length move in the opposite direction from particles with a different run length. For the arrays of L-shapes, we find that the application of a drift force can enhance a transverse rectification in the direction perpendicular to the drift. When particle-particle steric interactions are included, we find that the ratchet effects can be either enhanced or suppressed depending on barrier geometry, particle run length, and particle density.
I. INTRODUCTION
II. SIMULATION AND SYSTEM
III. FUNNEL-SHAPED BARRIERS
IV. L SHAPED BARRIERS
A. Steric Interactions
V. DISCUSSION
VI. SUMMARY
References

I.  INTRODUCTION

When Brownian particles are placed in an asymmetric potential substrate in the presence of an external ac drive, it is possible to realize a so-called "rocking ratchet" effect in which the particles undergo net dc motion [1,2,3]. Ratchet effects can also be realized using other forms of external driving such as by flashing the substrate on and off to create what is called a flashing ratchet [1,2,3]. In such ratchet systems, the Brownian motion is rectified due to a symmetry breaking such as the asymmetry in the substrate potential or barriers; however, the breaking of other symmetries can also lead to directional motion. Ratchets have been studied and experimentally realized for a variety of systems including colloidal particles on asymmetric substrates [4,5], vortices in type-II superconductors interacting with nanostructured pinning sites [6,7,8], and granular media on vibrated asymmetric substrates [9]. It is also possible to realize ratchet effects on symmetric substrates provided that the external driving has some form of asymmetry [10,11,12,13,14,15]. More recently, what has been termed "active ratchets" have been realized in systems where there is no external ac driving or flashing but where the particles are self-driven. Active matter systems contain self motile particles [16,17,18,19] and include biological systems such as swimming bacteria [20,21], moving cells [22,23], and flocks of birds or fish [24], as well as non-biological systems such as artificial swimmers [25,26,27] and self motile colloidal particles [28,29,30,31,32].
In an experiment by Galjada et al., when run-and-tumble swimming E. coli were placed in a microfabricated array of V-shaped funnels, the bacteria concentrated on the side of the container towards which the funnel openings were pointing, indicating the existence of a ratchet effect [21]. When non-swimming bacteria that undergo only weak Brownian motion were placed in the same funnel array, the ratchet effect was absent. Active ratchet effects have also been observed in funnel geometries for swimming animals as well as artificial swimmers [33]. Subsequent numerical studies showed that this ratchet behavior can be captured using a model of point particles that undergo run and tumble dynamics along with a barrier interaction rule stating that when the particles interact with a barrier they run along the barrier rather than reflecting off of it [34]. As the run length of the particles is increased, the ratchet effect also increases, while in the limit of Brownian motion the ratchet transport is lost. Other studies showed explicitly that the rectification is caused by the breaking of detailed balance that occurs when the particles interact with the barriers, and that the particles must spend a long enough time running along the barrier for rectification to occur [35,36]. For other types of barrier interactions such as reflection [35,37] or scattering [37], the rectification is lost. In these simulations it was also shown that the particles accumulate in funnel tips and along boundaries [35], a phenomenon that is also observed in experiments [21]. Active ratchets have been studied for other types of swimming organisms [38,39,40,41] such as crawling cells [23]. In these systems, when collective effects are included [40,42,43] a ratchet reversal can occur where for a certain range of parameters the particles ratchet along the easy direction of the funnel, while for other parameters the ratchet motion occurs against the easy flow direction [42]. It was recently proposed that active ratchet effects can arise on symmetrical substrates for certain models [44].
One of the most promising applications for active ratchets is sorting, where different species or particles with different run-and-tumble swimming lengths could be sorted due to the different speed or direction of motion through a ratchet geometry of one type of particle compared to another [45]. Variants on this type of ratchet effect have been harnessed to create active matter powered gears, where asymmetric gears immersed in an assembly of active matter particles exhibit rotation in a preferred direction [46,47]. There are also proposals to use asymmetric barriers to capture active matter particles [48]. In non-active matter systems another method for sorting Brownian particles in arrays is to apply a dc drift to the particles that forces them to move through a lattice of asymmetric obstacles. In this geometry, particles with different diffusion coefficients follow different trajectories through the array, such that the particle motion perpendicular to the drift force varies as a function of the diffusion coefficient [49,50,51]. This and related methods have been used to continuously sort particles such as DNA strands of different lengths using asymmetric post arrays [51,52,53,54,55]. There have also been several other studies on how to sort particles with different diffusion constants in periodic arrays when an additional dc drift is applied [55,56,57,58].
In this work we examine active ratchet systems in which the particles interact with an array of asymmetric barriers in the presence of an additional dc drift force. We consider run-and-tumble particles interacting with two barrier geometries. For an array of V shapes or funnels, in the absence of a drive the particles exhibit an active ratchet effect and move in the easy flow direction; however, when a dc drive is applied against the ratchet effect, we find a ratchet reversal, indicating that it should be possible to set the dc drive such that particles with different run lengths move in opposite directions through the funnels. The velocity-force curves contain nonlinear features that vary as the run length changes. For example, for a fixed dc drive applied against the easy flow direction, increasing the run length initially increases the flow of particles in the reversed ratchet direction as the trapping of particles at the funnel tips is reduced; however, at long run lengths the reversed motion in the direction of the dc drive is suppressed when the forward ratchet effect begins to dominate. We show that the ratchet effect can be controlled by applying a dc drive perpendicular to the the ratchet direction. Inclusion of steric interactions between particles reduces the ratchet effect, and the magnitude of the reduction increases as the size or density of the particles increases. For an array of even L-shaped barriers, application of a dc drive can increase the rectification transverse to the applied drive by almost an order of magnitude compared to the drive-free case. For this geometry, when steric interactions between the particles are included, the transverse ratchet effect is enhanced for some run lengths and particle densities and suppressed for others.

II.  SIMULATION AND SYSTEM

Fig1.png
Figure 1: (a) Sample geometry for the V shaped barrier array. In the absence of an external drive, run-and-tumble particles ratchet in the positive y-direction. The arrows indicate the two different directions in which the driving current can be applied (dx=0, dy=−1 and dx=1, dy=0). (b) Sample geometry for the even L-shaped barrier array. In this case, the dc drive is applied in the negative y-direction The arrow indicates the direction in which the driving current is applied (dx=0, dy=−1).
We consider a two-dimensional system of size L ×L containing N active matter particles obeying the same rules for run-and-tumble self-propelled motion and barrier interactions as previously used to study ratchets without a drift [34,37]. Steric particle-particle interactions are neglected in some sets of simulations and included in others. We employ periodic boundary conditions in the x and y-directions for samples containing a periodic array of V-shaped barriers as in Fig. 1(a) or a periodic array of even L-shaped barriers as in Fig. 1(b). For the V-shaped barriers, there are NB=24 barriers with side length ls=5.0, the V has an angle of 45°, and the barrier lattice constant is approximately a=20. For the even L-shaped barriers, there are NB=30 barriers with sides of equal length ls=4.9. In each case the system size is L=99 and there are N=980 particles. The dynamics of particle i are obtained by integrating the following overdamped equation of motion:
η d Ri
dt
 = Fmi + Fib + Fsi + Fdci .
(1)
Here the damping constant is η = 1.0 and Fmi is the motor force. We neglect hydrodynamic interactions. The run-and-tumble dynamics is modeled by having the particles move with a constant force Fm in a randomly chosen direction for a fixed run time τr; after this time, a new running direction is randomly chosen to represent the tumbling process. The tumbling occurs instantaneously. In the absence of interactions with barriers or other particles, a single particle would move a distance Rl = Fmτr during a single run time. The term Fbi represents the particle-barrier interaction force. The barrier exerts a short-range repulsion on the particle, modeled by a stiff finite range spring. As a result, when a particle strikes a barrier it moves along the barrier at a speed given by the component of its motor force that is parallel to the barrier [34,37] until it either reaches the end of the barrier or undergoes a tumbling event, when it has the opportunity to move away from the barrier or continue following the barrier at a new speed. A particle moving along a barrier can become trapped at corners where two barriers meet. The barrier thickness is equal to the particle radius Rp. The steric interaction between particles, Fis, when included, is modeled with a repulsive short-range harmonic force given by Fsi = ∑i ≠ jN k(Reffij − |rij|)Θ(Rijeff − |rij|)∧rij where the spring constant k = 200, rij = Ri − Rj, ∧rij = rij/|rij| and Rij = ri + rj, where Ri(j) is the location of particle i(j) and ri(j) is the radius of particle i(j). Here we consider particles of uniform size, ri=Rp. Unless otherwise noted, we take Rp=0.35. The dc force Fdci=Fdc(dx ∧x + dy∧y) is applied uniformly to all the particles. For dx=0 and dy=−1, in the absence of self-driven forces or barriers this drive would cause the particles to drift in the negative y direction. We measure the normalized average particle velocities 〈Vx〉 = (1/N)∑Ni = 1 vi·∧x and 〈Vy〉 = (1/N)∑Ni = 1 vi·∧y.
Fig2.png
Figure 2: (a) 〈Vy〉 vs particle run length Rl for the V-shaped barrier system in Fig. 1(a) with dx=0, dy=−1, and Fdc = 0, 0.05, 0.1, 0.2, 0.3, and 0.5, from top to bottom. At Fdc = 0 the system exhibits only a positive ratchet effect. Inset: The location of the minima in 〈Vy〉 from the main panel vs Fdc. (b) 〈Vy〉 vs Rl for the system with Fdc = 0.5 from (a) for periodic (dark curve) and randomized (light curve) positions of the barriers, showing strong overlap. (c) 〈Vy〉 vs Rl for the system with Fdc = 0.5 from (a) for different barrier densities with NB = 8 (lower line), 24 (center line), and 42 (upper line), showing that for increasing barrier density the curves shift up due to the increasing ratchet effect.

III.  FUNNEL-SHAPED BARRIERS

We first consider non-interacting particles in the array of V-shaped barriers illustrated in Fig. 1(a). In the absence of any external drive, this system shows a rectification effect similar to that observed for a single row of barriers [34] where for a finite run length Rl there is a net particle current in the easy flow direction of the funnels (positive y-direction) which increases with increasing Rl. In Fig. 2(a) we plot 〈Vy〉 versus run length Rl for a dc drive applied in the negative y direction (dx=0 and dy=−1), against the easy flow direction of the funnels. For each Rl we wait a sufficiently long time before measuring 〈Vy〉 to avoid any transient effects. Shown in Fig. 2(a) are the results for Fdc = 0, 0.05, 0.1, 0.2, 0.3, and 0.5. For Fdc = 0, 〈Vy〉 is initially zero for Rl = 0 and monotonically increases with increasing Rl, consistent with previous results [34]. At finite Fdc and small Rl, 〈Vy〉 is initially negative and rapidly becomes more negative as Rl increases until reaching a maximally negative value between Rl=1 and 10, after which it increases with increasing Rl. For Fdc = 0.05, 0.1, and 0.2, 〈Vy〉 crosses from negative to positive y-direction flow with increasing Rl when the positive y direction ratchet effect becomes large enough to overcome the drift force in the negative y direction. This result implies that in a mixed system of particles with short and long running lengths, there is a range of Fdc over which the particles with short running lengths would move in the negative y direction while the particles with long running lengths would move in the positive y direction. The initial decrease in 〈Vy〉 with increasing Rl at smaller values of Rl occurs because for small Rl the positive ratchet effect is weak, and many particles become trapped in the funnel tips due to the negative y drift force. For very small Rl, most or all of the particles are trapped, giving 〈Vy〉 ≈ 0 as shown in Fig. 2(a). As Rl increases, some particles can escape from the funnel tip traps but are then entrained by the drift force to move in the negative y direction, giving an increasingly negative value of 〈Vy〉 as more particles become mobile. In this regime, increasing the run length can increase the motion in direction of the drift force; however, for larger Rl, the positive ratchet effect begins to dominate the behavior and for large enough Rl the net flow is in the positive y direction.
We have also considered the effect of holding the barrier density constant but moving the barriers from ordered periodic to random positions. This is achieved by applying a randomized offset to the position of each barrier while avoiding barrier overlap. In Fig. 2(b) we plot 〈Vy〉 vs Rl for the Fdc = 0.5 case from Fig. 2(a) for the periodically and randomly placed barriers, where we find that the curves overlap almost completely. We observe the same lack of sensitivity to barrier placement for the other cases we have tested, indicating that the periodic placement of the barriers does not strongly affect the results in this work. Another quantity that we have varied is the barrier density, and in Fig. 2(c) we plot 〈Vy〉 vs Rl for samples of the same size with different numbers of barriers NB = 8, 24, and 42 at Fdc=0.5. For NB = 8, 〈Vy〉 is more strongly negative since more particles are able to move in the negative direction of the drift. As Rl increases, the value of 〈Vy〉 remains more negative for NB=8 than for NB=24 because the ratchet effect that tends to cause the particles to move in the positive y direction against the applied drift is smaller when the number of barriers is smaller. For NB = 42, 〈Vy〉 rises closer to zero as the ratchet effect becomes even stronger. For the other systems, we find a similar trend where changing the density of the barriers does not change the qualitative features of the transport curves but can induce a vertical shift due to increased or decreased ratchet effects.
Fig3.png
Figure 3: 〈Vy〉 vs Fdc for the system in Fig. 2 with Rl = 0.5, 1.0, 2.0, 3.0, 5.0, and 10.0, from top to bottom. For small Fdc the ratchet effect gives a positive 〈Vy〉. As Fdc increases, 〈Vy〉 becomes negative and then drops to zero as the particles become trapped in the funnel tips by the dc drive. Inset: The plot of the minima in 〈Vy〉 from the main panel for Fdc vs Rl.
In Fig. 3 we plot 〈Vy〉 versus Fdc for Rl = 0.5, 1.0, 2.0, 3.0, 5.0, and 10. At small Fdc, the ratchet effect produces a positive 〈Vy〉. For increasing Fdc, 〈Vy〉 crosses zero and becomes negative before reaching a maximally negative value. As Fdc increases further, particles begin to be trapped in the tips of the funnels, and at large enough Fdc all the particles are trapped and 〈Vy〉 = 0. As Rl increases, a larger Fdc must be applied for complete trapping to occur. These results show that the system produces highly nonlinear velocity force curves.
Fig4.png
Figure 4: 〈Vy〉 vs Rl for the V-shaped barrier system from Fig. 1(a) with a drive perpendicular to the ratchet direction, dx=1 and dy=0, for Fdc = 0, 0.5, 1.0, 1.25, 1.5, 2.0, 3.0, and 4.0, from top to bottom. For finite Fdc, 〈Vy〉 is initially negative for small values of Rl and becomes increasingly negative until the ratchet effect becomes strong enough to cause the particles to move in the positive y-direction.
In Figs. 2(a) and 3, 〈Vy〉 passes through a minimum as either Rl or Fdc is varied. In the inset of Fig. 2(a) we plot the minima from Fig. 2(a) for Rl vs Fdc. For increasing Rl the minimum increases linearly with Fdc. Since the applied drift is in the negative y-direction, the particles become trapped in the absence of any run and tumble dynamics. As Rl increases, the particles can escape from the traps and experience a drift in the negative y-direction; however, for larger Rl the magnitude of the competing ratchet effect in the positive y direction increases. A rough estimate for the location of the minimum in 〈Vy〉 can be obtained by noting that a particle trapped at a funnel tip that begins to run in the direction opposite to the applied drift force needs to move outside of the funnel during a single run event in order to have a high probability of escaping from the funnel. For the case of Fdc = 0.5 this occurs when Rl − Ldc > ls, where Ldc is the distance a particle would freely drift in the negative y-direction during a run interval and ls is the barrier side length. At a run length of Rl = 10, Ldc = 2.5, so the inequality is satisfied. For run lengths greater than this, the particle escapes from the funnel with high probability. In the inset of Fig. 3 we show the locations of the minima from Fig. 3, where a similar argument can be applied. The curve is linear at lower values of Rl but rolls over and begins to saturate for high Rl.
In Fig. 4 we plot 〈Vy〉 vs Rl for the same system but with Fdc applied in the positive x-direction (dx=1, dy=0), perpendicular to the ratchet flow direction. Here we show Fdc = 0, 0.5, 1.0, 1.25, 1.5, 2.0, 3.0, and 4.0. Due to the barrier shapes, the drift force can alter the motion of the particles in the ratchet or y direction even though the drift is applied perpendicular to this direction. As the particles drift in the positive x direction, they encounter the outer left surface of a V barrier and follow the barrier wall downward in the negative y direction before becoming free of the barrier, encountering another barrier, and again moving in the negative y direction. As Fdc increases, the magnitude of 〈Vy〉 rapidly decreases, and Fig. 4 shows that for Fdc ≥ 1.5, 〈Vy〉 is negative at small Rl but becomes positive for larger Rl when the ratchet effect becomes strong enough to dominate the particle motion. This indicates that with the correct choice of perpendicular dc drive, particles with different run lengths could be sorted, with one species of particles moving in the positive y direction and the other species moving in the negative y direction. For Rl = 0, 〈Vy〉 is zero since the particles no longer undergo diffusion and end up drifting only in the empty horizontal spaces separating adjacent rows of barriers.
Fig5.png
Figure 5: 〈Vy〉 vs Rp for the V-shaped barrier system from Fig. 1(a) with Fdc = 0 and steric particle-particle interactions for Rl = 70, 40, 30, 20, 10, and 5.0, from top to bottom. The ratchet effect decreases monotonically as Rp, and the effective density of the particles, increases.
Fig6.png
Figure 6: The particle positions (black dots) and barrier locations (red lines) for a subsection of the V-shaped barrier system from Fig. 1(a) with steric particle-particle interactions. (a) For Fdc = 0, Rl = 40, and Rp = 1.15, there is a crowding effect in the traps where at most three particles can fit in a trap. Additionally, a clustering effect begins to emerge. (b) For Fdc=0, Rl = 40, and Rp = 0.2, a much larger number of particles can be captured in the funnel tips.
We next consider the effects of steric repulsion on the ratchet effect in the absence of an external drive. In Fig. 5 we plot 〈Vy〉 versus the particle radius Rp for Rl = 70, 40, 30, 20, 10, and 5. In each case, inclusion of steric interactions causes a drop in the rectification effect due to trapping and clustering. Each funnel can now trap only a limited number of particles, since particles that would be trapped at the funnel tip in the noninteracting case instead fill up the funnel, reducing the trapping effectiveness for particles moving in the negative y direction. For example, in Fig. 6(a) we illustrate a subsection of a system with Fdc = 0, Rl = 40, and Rp = 1.15, where at most three particles can fit inside each V shaped barrier due to the finite size of the particles. We also observe a clustering of the particles that reduces their overall mobility. A similar dynamic clustering effect for repulsively interacting active particles has been studied as a function of particle density in simulations [59] and observed in experiments with active colloids [32]. In Fig. 6(b) we show a sample with Rp = 0.2, where a larger number of particles can be trapped in the V barriers. This reduces the net downward motion of the particles since particles traveling in the positive y-direction are not trapped by the barriers. As Rp increases, fewer particles can be trapped in each funnel, and the net downward motion of the particles increases. We also find that as the particle radius increases, there is a decrease in the extent to which the particles are guided along the sides of the barriers and pushed in the negative y direction, reducing the rectification. If two particles are moving along a barrier wall in opposite directions, the particles can block each others flow. In the system without steric interactions, the particles could instead pass through each other. As the particle radius increases, the number of particles that can be guided by a given barrier is reduced since fewer particles can fit on the barrier at the same time. An increase in the particle density produces a higher number of particle-particle collisions throughout the system, even in the regions away from the barriers, reducing the effective run length of the particles. When a drift is applied, an increase in the particle radius also monotonically decreases the ratchet effect.

IV.  L SHAPED BARRIERS

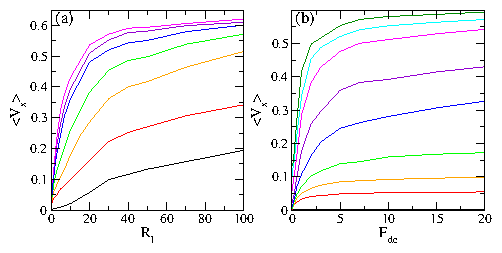
Fig7.png
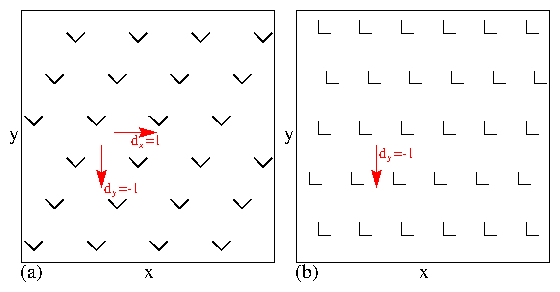
Figure 7: 〈Vx〉, the particle drift in the x direction, for the L-shaped barrier system from Fig. 1(b) with a dc drive applied in the negative y-direction (dx=0, dy=−1). (a) 〈Vx〉 vs Rl for Fdc = 0, 0.5, 1, 2.1, 5, 10, and 20 from bottom to top. At Fdc = 0 there is a ratchet effect in the positive y and x directions. As Fdc increases, 〈Vx〉 increases. (b) 〈Vx〉 vs Fdc for Rl = 0.1, 0.5, 1, 2, 5, 10, 20, 30, and 50, from bottom to top. Here the effectiveness of the rectification in the x-direction increases more strongly with increasing Fdc for smaller Rl.
Fig8.png
Figure 8: Subsections of the L-shaped barrier system in Fig. 7 where the dc drive is in the negative y-direction, dx=0 and dy=−1. Dots: particles; thick lines: barriers; lines: particle trajectories. (a) For small run length Rl = 0.01 at Fdc = 5.0, some particles accumulate on the barriers while the remaining particles move only in the regions between the barriers. (b) The trajectory of a single particle at Rl = 30 and Fdc = 1.0 shows that over time the particle drifts in the positive x-direction. Additionally, there are several instances where the particle moves along a barrier and is guided to move in the positive x-direction. (c) At Rl = 3.0 and Fdc = 7.0, the trajectories have a net tilt in the positive x-direction.
We next consider the even L shaped barriers illustrated in Fig. 1(b). In this geometry, for Fdc = 0 and increasing Rl the particles exhibit a ratchet effect in the positive y and x directions. We apply a dc drive in the negative y-direction, dx=0 and dy=−1, and measure the transport in the perpendicular or x-direction. In Fig. 7(a) we plot 〈Vx〉 vs Rl for systems with Fdc = 0, 0.5, 1, 2, 5, 10, and 20. At Fdc = 0, 〈Vx〉 increases with increasing Rl due to the ratchet effect. For increasing Fdc, 〈Vx〉 monotonically increases, indicating that a transverse ratchet effect occurs. This is illustrated more clearly in Fig. 7(b) where we plot 〈Vx〉 versus Fdc for Rl = 0.1, 0.5, 1.0, 2.0, 5, 10, 20, 30, and 50. The effectiveness of the x direction rectification increases the most rapidly with increasing Fdc for the smallest value of Rl: at Rl = 1 the ratio of the velocities for Fdc = 0 and Fdc = 20.0 is nearly 40, while at Rl = 5 it is 4.5. This result indicates that a significant increase in the transverse ratchet effect can be achieved in active ratchet systems by applying a drift current. For a system of noninteracting particles with a finite drift force, when Rl = 0 there is no transverse ratchet effect since the particles either pile up on the barriers or flow in the regions between the barriers, as illustrated in Fig. 8(a) for Rl = 0.01 and Fdc = 5.0. The mechanism by which the dc drift enhances the x-direction ratchet effect is illustrated in Fig. 8(b) for Rl = 30 and Fdc = 1.0, where we highlight the trajectory of a single particle. When the particle encounters the top of a barrier, it can move either along the outer (left) or inner (right) upper wall of the barrier. If the particle moves to the inner side of the barrier, it becomes stuck in the corner of the barrier until it undergoes a tumbling event that allows it to move away from the barrier in the positive x direction. Several instances of this trap-and-escape motion appear in Fig. 8(b). If the particle moves to the outer side of the barrier, it enters the region between barriers and is pushed in the negative y-direction by the dc drive until it encounters another barrier, at which point it can become trapped at the barrier corner before escaping and moving in the positive x-direction. This produces a net flux in the positive x-direction over time, as shown in Fig. 8(b). As Fdc is further increased, the particles that move along the outside walls of the barriers into the barrier-free regions travel more rapidly in the negative y direction and more quickly encounter additional barriers, increasing the effectiveness of the transverse ratchet effect. In Fig. 8(c), the particle trajectories for Rl = 3.0 and Fdc = 7.0 clearly show a tilt toward the positive x-direction. We also observe a particle trajectory shadow on the underside of each barrier.

A.  Steric Interactions

Fig9.png
Figure 9: 〈Vx〉 vs the particle radius Rp for the L-shaped barrier system from Fig. 7 with sterically interacting particles and Rl=2.0 at Fdc = 0.1, 0.25, 0.5, 1, 2, 3, 5, and 10, from bottom to top. For small Fdc, the steric interactions reduce the ratchet effect, while for larger Fdc there is a nonmonotonic response with a peak in 〈Vx〉 at Rp ≈ 0.8.
Fig10.png
Figure 10: Subsections of the L-shaped barrier system in Fig. 9 where the dc drive is in the negative y-direction, dx=0 and dy=−1. Dots: particles; thick lines: barriers; lines: particle trajectories. (a) Noninteracting particles with Rl = 2.0 and Fdc = 5.0 accumulate on the barriers. (b) For the interacting particle system with Rp = 0.7, Rl=2.0, and Fdc=5.0, fewer particles are trapped at the barriers.
We next consider the effects of including steric particle-particle interactions for the L-shaped barrier system from Fig. 7. In Fig. 9 we plot 〈Vx〉 versus the particle radius Rp for Rl = 2.0 and Fdc = 0.1, 0.25, 0.5, 1, 2, 3, 5, and 10. For small or zero Rl, the addition of steric interactions reduces the transverse ratchet effect as also found above for the V-shaped barriers. At higher values of Rl, however, the steric interactions can increase the ratchet effect when Fdc ≥ 0.5, with a maximum in 〈Vx〉 occurring at Rp ≈ 0.8. In all cases, for Rp > 0.9 the rectification effect decreases since fewer particles can fit on the barrier walls to experience guided motion. The initial increase in 〈Vx〉 at small Rp for the larger values of Fdc occurs due to the filling of the barriers by the particles, as illustrated for small Rl for the noninteracting particles in Fig. 8(a). When there are steric interactions, the number of particles that can be trapped by each barrier is reduced. In addition, the trapped particles are more likely to move in the positive x direction since the corner of the barrier becomes blocked by the earliest-arriving particles; thus, interacting particles that are trapped by a barrier tend to be pushed to the right in the positive x direction. Additionally, as particles arrive at the barrier from above, they fall onto the particles that are already trapped at the barrier and tend to create a sandpile-like sloped structure with the slope oriented in the positive x-direction. In Fig. 10(a) we plot the particles and their trajectories at Fdc = 5.0 and Rl = 2.0 for a system without steric interactions, where a pileup of particles on the barriers occurs. We show the same system with finite steric interactions and Rp = 0.7 in Fig. 10(b), where we find that fewer particles are trapped on the barriers due to the repulsive particle-particle interactions. In this case, particles arriving from above the barrier that interact with the barrier tend to be deflected in the positive x-direction, producing an enhanced rectification.
Fig11.png
Figure 11: 〈Vx〉 vs Rl for the L-shaped barrier system with sterically interacting particles from Fig. 9 at Fdc = 5.0 for Rp = 0.5, and Rp = 0.9 with steric interactions (solid lines from bottom left to top left). The dashed line is a system with Rp = 0.3 and no steric interactions. Here the particle-particle interactions enhance the rectification at the lower values of Rl and suppresses the rectification at higher values of Rl.
In general, inclusion of steric interactions enhances the rectification for shorter Rl, while at longer run lengths, the steric interactions decrease the ratchet effect. This is more clearly seen in Fig. 11 where we plot 〈Vx〉 versus Rl at Fdc = 5.0 for Rp = 0.3, 0.5, and 0.9 as well as for a system without steric interactions with Rp=0.3. Here for Rl < 5.0 the rectification is enhanced by the steric interactions while for Rp > 5.0, 〈Vx〉 is higher for the noninteracting particles. At finite Fdc and low Rl, the noninteracting particles accumulate in the barriers, reducing the ratchet effect, while the addition of steric interactions reduces the number of particles that can interact with each barrier. At larger Rl for the noninteracting case, the particles do not accumulate in the barriers but there is no limit to the number of particles that can interact with the barriers, while when steric interactions are present, the number of opportunities for particles to interact with the barriers is limited.
Fig12.png
Figure 12: 〈Vx〉 vs ρ for the L-shaped barrier system from Fig. 9 with sterically interacting particles (curved lines, black) and noninteracting particles (flat lines, red). Here L is held fixed, ρ = N/L2, and Rp = 0.5. In all cases 〈Vx〉 is independent of ρ for the noninteracting particles. At small ρ where there are few particle collisions, the 〈Vx〉 curves for the interacting and noninteracting particles are identical or nearly identical. (a) At Fdc = 1.0 and Rl = 1.0, the ratchet efficiency for the interacting particle system increases with increasing ρ and is always higher than in the noninteracting particle system. (b) At Fdc = 1.0 and Rl = 60, the ratchet effect for the interacting particles is reduced with increasing ρ and is always lower than for the noninteracting particle system. (c) At Rl = 1.0 and Fdc = 10, the ratchet effect increases with increasing ρ for the interacting particles. (d) At Rl = 60 and Fdc = 10, the ratchet effect decreases with increasing ρ for the interacting particles.
We can also examine the effects of the steric interactions by holding Rp and L fixed and varying N to change the particle density, ρ = N/L2. For the noninteracting case, 〈Vx〉 is independent of ρ. In Fig. 12(a) we plot 〈Vx〉 versus ρ for a system with Rp=0.5, Fdc = 1.0 and Rl = 1.0. The result for the noninteracting particles is a flat line. At low densities where there are almost no particle-particle collisions, the value of 〈Vx〉 for the interacting and noninteracting systems are almost identical. As ρ increases, 〈Vx〉 increases for the interacting particle system until reaching a plateau. For values of ρ higher than shown in the figure, 〈Vx〉 eventually decreases again as the overall system mobility decreases and the system crystallizes. Figure 12(b) shows the same system with Rl = 60. At low densities we again find that 〈Vx〉 for the interacting and noninteracting systems are almost the same; however, as ρ increases, 〈Vx〉 for the interacting system decreases. In Fig. 12(c) we show a system with Rl = 1.0 and Fdc = 10, where 〈Vx〉 for the interacting system increases with increasing ρ, while Fig. 12(d) shows that for Rl = 60 and Fdc=10, 〈Vx〉 for the interacting system decreases with increasing ρ. The case in Fig. 12(d) is interesting since it shows non-monotonic behavior where the steric interactions initially increase the transverse ratchet effect at low densities. This is due to the large Fdc which forces all of the particles onto the bottom of the L barriers, causing more of the particles to be trapped in the corner of the L. The inclusion of steric interactions forces the particles to spread out along the bottom of the L, increasing the chance that some of these particles will fall off and thus be translated in the positive x direction. When Rl is large, this effect is small, and for increasing density a smaller fraction of the particles can interact with the barriers, diminishing the transverse ratchet effect.
These results show that steric interactions in combination with a dc drive and short but finite run lengths increase the transverse ratchet effect, while for long run lengths the steric interactions decrease the ratchet effect. This indicates that it should be possible to use the L-shaped barriers to sort particles based on both run length and particle radius.

V.  DISCUSSION

We note that many studies of active ratchet systems have considered swimming bacteria which have a rod-like shape. In our previous simulation study of run and tumble swimmers [43], we considered point-like particles and captured the same behaviors found in the experiment with rod-like bacteria [21]. Another system that can be well approximated by spherical particles is self-driven colloids or Janus particles [29,60], which can be manipulated in many cases with magnetic fields. Simulations for Janus particles in asymmetric geometries have produced strong ratchet effects [61], indicating that Janus particles should be a promising system in which to explore active drift ratchets.
In our work we did not consider the possible role of hydrodynamics. Hydrodynamic effects can arise due to the swimming of the microorganisms [62,63], and can lead to synchronization effects [64] or the creation of large scale features such as turbulent type flows [65]. Hydrodynamic coupling is expected to be weak or negligible for cells moving on a surface [66], while proximity to a hard wall can screen the hydrodynamic coupling [67,68] and confinement between two walls causes the hydrodynamic coupling to fall off more quickly with distance than in bulk [69,70]. Particles that remain a constant distance from a substrate have a diffusion coefficient that is determined by this distance [71]. When a particle is externally driven such as with an optical trap, the flow field can be monopole-like, whereas internally driven or active particles are proposed to have dipolar or higher order multipolar hydrodynamic interactions. This proposal was tested experimentally in Ref. [72], where it was shown that at large distances the hydrodynamic interactions are washed out by rotational diffusion of the swimming direction. This lends support to the groups that have neglected hydrodynamic interactions in their modeling [41,46,73] The presence of many interacting particles also tends to randomize the effects of hydrodynamic interactions, which may have the same effect as random tumbling of the particles [74]. It is possible that hydrodynamics could play a role in an experimental system, although the detailed nature of this role remains a topic of active study. We note that there have been numerous examples in which predictions from simulations such as ours which neglect hydrodynamic interactions have been found to agree very well with experimental observations, including our own work in Ref. [34] that captured the behavior found experimentally for dilute bacteria in Ref. [21], so we expect that at least some of the features we describe should be readily observable in colloidal experiments. Future studies could explore the role of hydrodynamic interactions, either by including additional hydrodynamic entrainment by the walls, or by incorporating pairwise tensorial forces in the particle interactions. Another possibility would be to consider large collections of swimmers that create vortex or swarming structures, which could induce new effects. Other directions to explore include mixtures of different swimming species or mixtures of active and nonactive particles, or changing the locomotion of the active particles from run-and-tumble to push or pull locomotion. Experimentally it might also be interesting to consider crawling eukaryotic cells, where the external driving could be applied using chemotatic drift or chemical gradients.

VI.  SUMMARY

We have investigated self-driven particles undergoing run-and-tumble dynamics in the presence of arrays of V- and L- shaped barriers. For the V-shaped barriers in the absence of a drive, we find a spontaneous ratchet effect where the particles have a net motion in the easy flow direction of the barriers. The efficiency of this ratchet effect increases with increasing run length, as found in earlier studies of single rows of barriers and in experiments. When we apply a dc drift force in the direction opposite to this ratchet effect, we obtain nonlinear velocity-dc force response curves. We also observe regimes in which particles with different run lengths move in opposite directions. The introduction of steric particle-particle interactions monotonically reduces the ratchet effect. For the even L-shaped barriers, which have both arms the same length, we measure the particle velocity in the direction perpendicular to the dc drive and find a transverse ratchet effect that can be substantially enhanced by the dc drive. The inclusion of steric interactions can also increase the magnitude of the transverse ratchet effect. When the particle radii become too large, this increase is suppressed since fewer particles can interact with each barrier. The increase in the transverse ratchet effect occurs for systems with small but finite run lengths and intermediate particle densities or radii. When the run lengths are long, the addition of steric interactions generally reduces the ratchet effect. Our results show that under a dc drift, active ratchet effects can be substantially enhanced, and provide another approach for controlling the sorting of active matter. We also find that steric interactions can in some cases produce an increase in the ratchet effectiveness.
This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396.

References

[1]
P. Reimann, Phys. Rep. 361, 57 (2002).
[2]
R.D. Astumian and P. Hänggi, Phys. Today 55(11), 33 (2002).
[3]
P. Hänggi and F. Marchesoni, Rev. Mod. Phys. 81, 387 (2009).
[4]
J. Rousselet, L. Salome, A. Ajdari, and J. Prost, Nature 370, 446 (1994).
[5]
K. Xiao, Y. Roichman, and D.G. Grier, Phys. Rev. E 84, 011131 (2011).
[6]
C.S. Lee, B. Jankó, I. Derényi, and A.L. Barabási, Nature (London) 400, 337 (1999).
[7]
C.C. de Souza Silva, J. Van de Vondel, B.Y. Zhu, M. Morelle, and V.V. Moshchalkov, Phys. Rev. B 73, 014507 (2006); W. Gillijns, A.V. Silhanek, V.V. Moshchalkov, C.J. Olson Reichhardt, and C. Reichhardt, Phys. Rev. Lett. 99, 247002 (2007); Q. Lu, C.J. Olson Reichhardt, and C. Reichhardt, Phys. Rev. B 75, 054502 (2007); L. Dinis, D. Perez de Lara, E.M. Gonzalez, J.V. Anguita, J.M.R. Parrondo, and J.L. Vicent, New J. Phys. 11, 073046 (2009).
[8]
B.L.T. Plourde, IEEE Trans. Appl. Supercond. 19, 3698 (2009).
[9]
Z. Farkas, P. Tegzes, A. Vukics, and T. Vicsek, Phys. Rev. E 60, 7022 (1999); J.F. Wambaugh, C. Reichhardt, and C. J. Olson, Phys. Rev. E 65, 031308 (2002); Z. Farkas, F. Szalai, D.E. Wolf, and T. Vicsek, Phys. Rev. E 65, 022301 (2002).
[10]
S.-H. Lee and D.G. Grier, Phys. Rev. E 71, 060102 (2005).
[11]
A. Libál, C. Reichhardt, B. Jankó, and C. J. Olson Reichhardt, Phys. Rev. Lett. 96, 188301 (2006).
[12]
C. Reichhardt, C.J. Olson, and M.B. Hastings, Phys. Rev. Lett. 89, 024101 (2002); C. Reichhardt and C. J. Olson Reichhardt, Phys. Rev. E 68, 046102 (2003).
[13]
R. Guantes and S. Miret-Artés, Phys. Rev. E 67, 046212 (2003).
[14]
P. Tierno, T.H. Johansen, and T.M. Fischer, Phys. Rev. Lett. 99, 038303 (2007).
[15]
D. Speer, R. Eichhorn, and P. Reimann, Phys. Rev. Lett. 102, 124101 (2009).
[16]
B ten Hagen, S. van Teeffelwn, and H. Löwen, J. Phys: Condens. Matter 23, 194119 (2011).
[17]
P. Romanczuk, M. Bär, W. Ebeling, B. Lindner, and L. Schimansky-Geier, Eur. Phys. J. Special Topics 202, 1 (2012).
[18]
S. Ramaswamy, Ann. Rev. Condens. Matter Phys. 1, 323. (2010)
[19]
M.C. Marchetti, J.F. Joanny, S. Ramaswamy, T.B. Liverpool, J. Prost, M. Rao, and R.A. Simha, Rev. Mod. Phys. 85, 1143 (2013).
[20]
H. C. Berg, Random Walks in Biology (Princeton University Press, Princeton, NJ, 1983).
[21]
P. Galajda, J. Keymer, P. Chaikin, and R. Austin, J. Bacteriol. 189, 8704 (2007).
[22]
D. Bray, Cell Movements: from Molecules to Motility (Garland Publ., New York, 1992)
[23]
G. Mahmud, C.J. Campbell, K.J.M. Bishop, Y.A. Komarova, O. Chaga, S. Soh, S. Huda, K. Kandere-Grzybowska, and B.A. Grzybowski, Nature Phys. 5, 606 (2009).
[24]
T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen, and O. Shochet, Phys. Rev. Lett. 75, 1226 (1995); G. Grégoire and H. Chaté, Phys. Rev. Lett. 92, 025702 (2004).
[25]
R. Dreyfus, J. Baudry, M.L. Roper, M. Fermigier, H.A. Stone, and J. Bibette, Nature 437, 862 (2005).
[26]
S.J. Ebbens and J.R. Howse, Soft Matter 6, 726 (2011).
[27]
G. Lumay, N. Obara, F. Weyer, and N. Vandewalle, Soft Matter 9, 2420 (2013).
[28]
J.R. Howse, R.A.L. Jones, A.J. Ryan, T. Gough, R. Vafabakhsh, and R. Golestanian, Phys. Rev. Lett. 99, 048102 (2007).
[29]
H.-R. Jiang, N. Yoshinaga, and M. Sano, Phys. Rev. Lett. 105, 268302 (2010).
[30]
G. Volpe, I. Buttinoni, D. Vogt, H. Kümmerer, and C. Bechinger, Soft Matter 7, 8810 (2011).
[31]
I. Buttinoni, G. Volpe, F. Kümmel, G. Volpe, and C. Bechinger, J. Phys.: Condens. Matter 24, 284129 (2012).
[32]
J. Palacci, S. Sacanna, A.P. Steinberg, D.J. Pine, and P.M. Chaikin, Science 339, 936 (2013); I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger, and T. Speck, Phys. Rev. Lett. 110, 238301 (2013).
[33]
P. Galajda, J. Keymer, J. Dalland, S. Park, S. Kou, and R. Austin, J. Mod. Opt. 55, 3413 (2008).
[34]
M.B. Wan, C.J. Olson Reichhardt, Z. Nussinov, and C. Reichhardt, Phys. Rev. Lett. 101, 018102 (2008).
[35]
J. Tailleur and M.E. Cates, Europhys. Lett. 86, 60002 (2009).
[36]
M.E. Cates, Rep. Prog. Phys. 75, 042601 (2012).
[37]
C.J. Olson Reichhardt, J. Drocco, T. Mai, M.B. Wan, and C. Reichhardt, Proc. SPIE 8097, 80970A (2011).
[38]
V. Kantsler, J. Dunkel, M. Polin, and R.E. Goldstein, Proc. Natl. Acad. Sci. (USA) 110, 1187 (2013).
[39]
I. Berdakin, Y. Jeyaram, V.V. Moshchalkov, L. Venken, S. Dierckx, S.J. Vanderleyden, A.V. Silhanek, C.A. Condat, and V.I. Marconi, Phys. Rev. E 87, 052702 (2013).
[40]
G. Lambert, D. Liao, and R.H. Austin, Phys. Rev. Lett. 104, 168102 (2010).
[41]
L. Angelani, A. Costanzo, R. Di Leonardo, EPL 96, 68002 (2011).
[42]
J.A. Drocco, C.J. Olson Reichhardt, and C. Reichhardt, Phys. Rev. E 85, 056102 (2012).
[43]
M.B. Wan, and Y.S. Jho, Soft Matter 9, 3255 (2013).
[44]
A. Pototsky, A. M. Hahn, and H. Stark, Phys. Rev. E 87, 042124 (2013).
[45]
M. Mijalkov and G. Volpe, Soft Matter 9, 6376 (2013).
[46]
L. Angelani, R. Di Leonardo, and G. Ruocco, Phys. Rev. Lett. 102, 048104 (2009).
[47]
R. Di Leonardo, L. Angelani, D. Dell'Arciprete, G. Ruocco, V. Iebba, S. Schippa, M. P. Conte, F. Mecarini, F. De Angelis, and E. Di Fabrizio, Proc. Natl. Acad. Sci. (USA) 107, 9541 (2010); A. Sokolov, M.M. Apodaca, B.A. Grzyboski, and I.S. Aranson, Proc. Natl. Acad. Sci. (USA) 107, 969 (2010).
[48]
A. Kaiser, H.H. Wensink, and H. Löwen, Phys. Rev. Lett. 108, 268307 (2012); A. Kaiser, K. Popowa, H.H. Wensink, and H. Löwen, arXiv:1307.0030.
[49]
T.A.J. Duke and R.H. Austin, Phys. Rev. Lett. 80, 1552 (1998).
[50]
D. Ertas, Phys. Rev. Lett. 80 1548 (1998).
[51]
C.F. Chou, O. Bakajin, S.W.P. Turner, T.A.J. Duke, S.S. Chan, E.C. Cox, H.G. Craighead, and R.H. Austin, Proc. Natl. Acad. Sci. (USA) 96, 13762 (1999).
[52]
L.R. Huang, P. Silberzan, J.O. Tegenfeldt, E.C. Cox, J.C. Sturm, R.H. Austin, and H.G. Craighead, Phys. Rev. Lett. 89, 178301 (2002).
[53]
L.R. Huang, E.C. Cox, R.H. Austin, and J.C. Sturm, Science 304, 987 (2004).
[54]
K. Loutherback, J. Puchalla, R.H. Austin, and J.C. Sturm, Phys. Rev. Lett. 102, 045301 (2009).
[55]
Z. Li and G. Drazer, Phys. Rev. Lett. 98, 050602 (2007).
[56]
R. Eichhorn, J. Regtmeier, D. Anselmetti, and P. Reimann, Soft Matter 6, 1858 (2010).
[57]
D. Reguera, A. Luque, P. S. Burada, G. Schmid, J. M. Rubí, and P. Hänggi, Phys. Rev. Lett. 108, 020604 (2012).
[58]
L. Bogunovic, M. Fliedner, R. Eichhorn, S. Wegener, J. Regtmeier, D. Anselmetti, and P. Reimann, Phys. Rev. Lett. 109, 100603 (2012).
[59]
S. Henkes, Y. Fily, and M.C. Marchetti, Phys. Rev. E 84, 040301 (2011); F.D.C. Farrell, M.C. Marchetti, D. Marenduzzo, and J. Tailleur, Phys. Rev. Lett. 108, 248101 (2012)
[60]
L. Baraban, M. Tasinkevych, M.N. Popescu, S. Sanchez, S. Dietrich, and O.G. Schmidt, Soft Matter 8, 47 (2012); S. Ebbens, M.H. Tu, J.R. Howse, and R. Golestanian, Phys. Rev. E 85, 020401 (2012); L. Baraban, D. Makarov, R. Streubel, I. Monch, D. Grimm, S. Sanchez, and O.G. Schmidt, ACS Nano 6, 3383 (2012); T. Bickel, A. Majee, and A. Wurger, Phys. Rev. E 88, 012301 (2013); W. Yang, V.R. Misko, K. Nelissen, M. Kong, and F.M. Peeters, Soft Matter 8, 5175 (2012); X Zheng, B ten Hagen, A. Kaiser, M. Wu, H. Cui, Z. Silber-Li, and H. Löwen, Phys. Rev. E 88, 032304 (2013).
[61]
P.K. Ghosh, V.R. Misko, F. Marchesoni, and F. Nori, Phys. Rev. Lett. 110, 268301 (2013).
[62]
E. Lauga and T.R. Powers, Rep. Prog. Phys. 72, 096601 (2009).
[63]
R. Ledesma-Aguilar and J.M. Yeomans, Phys. Rev. Lett. 111, 138101 (2013).
[64]
R. Golestanian, J.M. Yeomans, and N. Uchida, Soft Matter 7, 3074 (2011).
[65]
L.H. Cisneros, J.O. Kessler, S. Ganguly, and R.E. Goldstein, Phys. Rev. E 83, 061907 (2011); H.H. Wensink, J. Dunkel, S. Heidenreich, K. Drescher, R.E. Goldstein, H. Löwen, and J.M. Yeomans, Proc. Natl. Acad. Sci. (USA) 109, 14308 (2012); A. Sokolov and I.S. Aranson, Phys. Rev. Lett. 109, 248109 (2012); J. Dunkel, S. Heidenreich, K. Drescher, H.H. Wensink, M. Bär, and R.E. Goldstein, Phys. Rev. Lett. 110, 228102 (2013).
[66]
Y. Fily and M.C. Marchetti, Phys. Rev. Lett. 108, 235702 (2012).
[67]
E.R. Dufresne, T.M. Squires, M.P. Brenner, and D.G. Grier, Phys. Rev. Lett. 85, 3317 (2000).
[68]
H. Diamant, B. Cui, B. Lin, and S.A. Rice, J. Phys.: Condens. Matter 17, S2787 (2005).
[69]
B. Cui, H. Diamant, and B. Lin, Phys. Rev. Lett. 89, 188302 (2002).
[70]
G.I. Menon and S. Ramaswamy, Phys. Rev. E 79, 061108 (2009).
[71]
A. Fortini and M. Schmidt, Phys. Rev. E 83, 041411 (2011).
[72]
K. Drescher, J. Dünkel, L.H. Cisneros, S. Ganguly, and R.E. Goldstein, Proc. Natl. Acad. Sci. (USA) 108, 10940 (2011).
[73]
S. van Teeffelen and H. Löwen, Phys. Rev. E 78, 020101(R) (2008); H.H. Wensink and H. Löwen, Phys. Rev. E 78, 031409 (2008); G.S. Redner, A. Baskaran, and M.F. Hagan, Phys. Rev. E 88, 012305 (2013).
[74]
S.D. Ryan, A. Sokolov, L. Berlyand, and I.S. Aranson, New J. Phys. 15, 105021 (2013).


File translated from TEX by TTHgold, version 4.00.

Back to Home