Physical Review E 88, 042306 (2013)

Dynamics and Separation of Circularly Moving Particles in Asymmetric Patterned Arrays

C. Reichhardt and C. J. Olson Reichhardt

Theoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545 USA

(Received 2 July 2013; revised manuscript received 6 September 2013; published 14 October 2013)

There are many examples of driven and active matter systems containing particles that exhibit circular motion with different chiralities, such as swimming bacteria near surfaces or certain types of self-driven colloidal particles. Circular motion of passive particles can also be induced with an external rotating drive. Here we examine particles that move in circles and interact with a periodic array of asymmetric L-shaped obstacles. We find a series of dynamical phases as a function of swimming radius, including regimes where the particle motion is rectified, producing a net dc motion. The direction of the rectification varies with the swimming radius, permitting the separation of particles with different swimming radii. Particles with the same swimming radius but different chirality can also move in different directions over the substrate and be separated. The rectification occurs for specific windows of swimming radii corresponding to periodic orbits in which the particles interact one or more times with the barriers per rotation cycle. The rectification effects are robust against the addition of thermal or diffusive effects, and are in some cases even enhanced by these effects.
I. INTRODUCTION
II. SIMULATION AND SYSTEM
III. RECTIFICATION EFFECTS
A. Opposite chirality
IV. THERMAL EFFECTS
V. OTHER GEOMETRIES
A. Barrier lengths
VI. SUMMARY
References


I.  INTRODUCTION

Ratchet effects can occur for particles interacting with asymmetric substrates if the substrate is flashed on and off periodically or if an external ac drive is applied, and result in a net dc motion of the particles that is typically aligned with the direction of the substrate asymmetry [1]. When the particles interact with each other as well as the substrate, the ratchet effect can exhibit reversals where the particles move with the substrate asymmetry in some regimes, and against it in others [1]. It is also possible to create ratchet effects for particles moving over two dimensional (2D) symmetric substrates by driving the particles with two different ac drives that sum together to create an asymmetric pattern of particle motion [2,3,4,5,6]. Directed motion on periodic substrates has been demonstrated experimentally for colloidal particles driven over magnetic substrates [7,8].
More recently, ratchet effects have been observed in the absence of an external drive for systems of self-driven particles, termed active matter. Examples of active matter include swimming bacteria and crawling cells [9,10,11]. Numerous realizations of artificial active matter have been created experimentally for self driven colloidal systems [12,13,14,15,16,17,18]. Active matter ratchet effects have been obtained for swimming bacteria in an asymmetric funnel array in experiments [10], theory and simulations [19,20], as well as for other types of swimming organisms[21,22,23] and eukaryotic cells [11]. There has also been a recent proposal to rectify active particles interacting with symmetric substrates [24]. Variants on the active matter ratchet have been used to create active matter-powered gears [25].
The dynamics of active matter particles are often described by run and tumble motion where the particles move for a persistence length or periodic time before reorienting, or the particles may move in a persistent random walk [26,27]. In other active matter systems, the particles undergo circular motion such as found in swimming bacteria near surfaces [28,29,30] and other types of swimming cells [31,32]. A variety of circle swimmers have been studied theoretically and in simulations [33,34,35,36], and in recent experiments, it was demonstrated how to create artificial chiral colloidal moving particles that swim in circles with a fixed chirality depending on the asymmetric nature of the particle itself [37]. There are also proposals for creating molecular-sized chiral microswimmers by combining chiral molecules with chiral propellers [38]. An understanding of the novel types of dynamics that arise for circularly swimming particles interacting with patterned substrates could lead to the ability to control the motion of such systems, which could be used for separation techniques or to extract work from active matter. Recently, it was shown that artificial swimmers in a periodic substrate array prefer to swim along certain symmetry directions of the array [16], while Mijalkov and Volpe recently proposed a method for sorting circle swimmers moving with opposite chirality by using a substrate of chiral flower patterns or by having the particles move in channels of asymmetric arrays [38].
In this work we examine circularly swimming particles interacting with an array of L-shaped barriers that create an asymmetric landscape. The particles experience only contact interactions with the barriers, as in previous studies of run and tumble swimmers in asymmetric arrays [19]. After contacting a barrier, the particle motion normal to the barrier is suppressed, and the particle swims along the barrier according to its swimming force component that is parallel to the barrier, moving at reduced speed until reaching the end of the barrier or tumbling away from it. In the absence of a substrate, the particles show no dc drift; however, when a barrier array is present, we observe a series of regimes in which the particles form periodic orbits that produce net dc motion. We find that the directed motion remains locked over specific ranges of the swimming radii. In 2D, the particle motion is generally locked along particular symmetry directions of the array, but the direction of the motion may switch as the swimming radius varies. We also find that for certain values of the swimming radius, there is no dc motion and the particle orbits are localized. The fact that the magnitude and the direction of the dc motion can be controlled by varying the swimming radius indicates that this type of substrate could be used to separate particles with different swimming radii. When the chirality of the swimmers is reversed, a different set of directed motion regimes appears, permitting particles with the same swimming radius but different chirality to be separated. We find that the directed motion is generally reduced when the thermal fluctuations increase; however, there are regimes in which the directed motion is enhanced by the additional fluctuations. We demonstrate these effects for oblique and square arrays of even L-shaped barriers as well as for a square array of simple one-dimensional (1D) barriers.
Experimentally, such systems could be realized in microfabricated environments with barriers made out of silicon. For example, experiments on bacteria swimming through funnel barrier arrays employed silicon barriers that were 30 micrometers long and about 4 micrometers thick [10]. Specific active matter systems in which the effects we describe could be realized include artificial circle swimmers, colloidal particles subjected to external circular drives, and biological systems such as circularly swimming bacteria. We note that circularly moving particles interacting with symmetric two-dimensional substrates have also been shown to exhibit ratchet effects [3]; however, this system required an additional dc drive and/or asymmetry in the circular driving in order to produce ratchet motion. In the present work, no dc drive or alterations of the circular drive are needed since the asymmetry necessary to create the ratchet effect is provided by the barrier array. As a result, the system we describe here should be straightforward to study since it only requires placing some type of circularly moving particles into a barrier array.
Fig1.png
Figure 1: Sample geometries. (a) Oblique array of even L-shaped barriers. (b) Square array of even L-shaped barriers. (c) Square array of line barriers.


II.  SIMULATION AND SYSTEM

We consider a 2D system with periodic boundary conditions in the x and y-directions containing a periodic array of even L-shaped barriers, as illustrated in Fig. 1(a,b). In the even L shape, both arms of the L are identical in length. We refer to these barriers as "L-shaped" in the remainder of the paper. The particles are initialized at random positions in the free regions between barriers; in this work, we do not consider the effects of particle-particle interactions. The dynamics of particle i is governed by the following overdamped equation of motion:
η d Ri
dt
 = Fim + Fib + Fdc + ξTi.
(1)
Here η = 1 is the damping constant, Fm is the motor force, Fb is the force from interactions with the barriers, Fdc is an external drift force, and ξT is the thermal force. The motor force drives each particle in a circular manner with Fmi = si[Axcos(ωt)∧x + Aysin(ωt)∧y], where A ≥ 0 and si=±1 is the sign of the rotation. In the absence of a substrate, for Ax=Ay=A and si=1 the particle moves in a counterclockwise orbit forming a circle with radius A/ηω; for si=−1, the motion is clockwise. The barriers are composed of elongated repulsive walls terminating in repulsive truncated parabolas. Each barrier wall produces a short range steric repulsion of the particles given by Fbi=∑k=1Nb[(fbrik⊥/rb)Θ(rb−rik⊥)∧pk⊥ +(fbrik±/rb)Θ(rb−rik±)∧rik], where Nb is the number of barrier walls (each L shape is composed of two barrier walls), fb=30 is the strength of the barrier repulsion, rb=0.3 is the barrier radius or width, rik⊥ is the perpendicular distance from the particle to the line parallel to the barrier wall (set to zero if the intersection point of this perpendicular line does not fall on the barrier wall), rik±=|ri−rkp ±(l/2) ∧pk|||, rkp is the location of the center of the barrier wall, l is the length of the barrier wall, ∧pk⊥(||) is a unit vector perpendicular (parallel) to the axis of barrier k, and ∧rik=(ri−rik±)/|ri−rik±|. A particle in contact with a barrier moves along the barrier with the component of Fm that is parallel to the barrier until it reaches the end of the barrier or the orientation of Fm changes enough to move the particle away from the barrier. This is the same type of barrier interaction used in Ref. [19], and the sliding of particles along the barriers is also consistent with experimental observations of swimming bacteria. The thermal kicks come from the Langevin noise term ξT with the properties 〈ξT(t)〉 = 0 and 〈ξTi(t)ξjT(t′)〉 = 2ηkBTδijδ(t − t′), where kB is the Boltzmann constant. We report the thermal forces in terms of FT=√{2ηkBT}.
We focus on systems of size L ×L with L = 99 in dimensionless units, and with barrier lattice constants of around a = 20. The side length of the barriers is l=5 for most of the results presented here. A length scale can also be associated with the circular motion, so that for A = 1.0, a single particle in the absence of any barriers moves in a circle of radius 16. We have run larger system sizes and find that all our results are robust. We have studied different lattice constants for fixed system size and find the same results; however, there is a systematic shift of the rectification regime to lower ac amplitudes as the barrier lattice constant is reduced. We consider three substrate types: an oblique array of L-shaped barriers [Fig. 1(a)], a square array of L-shaped barriers [Fig. 1(b)], and a square array of simple 1D barriers [Fig. 1(c)]. For the L-shaped barriers, the lack of rotational symmetry in the system produces different motion for particles with different chiralities, which is important for separation. The system with simple 1D barriers has a rotational symmetry and is used to clarify the effect of breaking rotational symmetry by comparison with the L-shaped barrier systems. We place N = 980 non-interacting particles in the sample and measure the average particle velocities 〈Vx〉 = (1/N)∑Ni = 1 vi·∧x and 〈Vy〉 = (1/N)∑Ni = 1vi·∧y. At finite temperature, the use of this number of particles allows for sufficient averaging that a clear signature of a dc response can be obtained. If there is no net dc drift, then 〈Vy〉 = 0 and 〈Vx〉 = 0. In the absence of a substrate, the average velocities are always zero.
Fig2.png
Figure 2: (a) 〈Vy〉 vs A and (b) 〈Vx〉 vs A for the system with the oblique L-shaped barrier array shown in Fig. 1(a) for counterclockwise swimming particles with si=1. The light (red) curves centered at 〈Vy〉 = 0 and 〈Vx〉 = 0 are for the case where there is only an ac drive in the y-direction, Ay=A and Ax=0. The dark (black) curves are for circular swimmers with Ax=Ay=A. For the circular swimmers, there are a series of intervals of A where there is a net dc motion, and in several of these regions the velocities are constant or locked. The letters a-f indicate the values of A at which the particle trajectories in Fig. 4 were obtained.
Fig3.png
Figure 3: The trajectories of a single particle in the localized regimes for the system in Fig. 2 with counterclockwise swimming particles. L-shapes: barriers; dot: individual particle; line: particle trajectory. (a) A=0.49. (b) A=0.9. (c) A=1.2.
Fig4.png
Figure 4: The trajectories of a single particle in selected rectification phases for the system in Fig. 2 with counterclockwise swimming particles. The letters a-f in Fig. 2 correspond to the orbits shown in panels (a-f). L-shapes: barriers; dot: individual particle; line: particle trajectory. At (a) A = 0.57, (b) A=0.75, and (c) A=1.6, the particle translates in the positive y and x directions and interacts with the barriers once per cycle. (d) At A = 1.9, the particle moves in the positive y and negative x directions and interacts with the barriers twice per cycle. (e) At A = 2.05 the particle moves in the negative x direction while interacting with the barriers once per cycle. (f) At A = 2.5 the particle moves in the positive y and x directions and interacts with the barriers three times per cycle.


III.  RECTIFICATION EFFECTS

We first focus on the oblique geometry shown in Fig. 1(a) with si=1 so that the particles move in a counterclockwise direction. In Fig. 2(a) we plot 〈Vy〉 vs A for this system in the absence of thermal forces, FT=0. As A increases, the radius of the circular path that the particle would follow in the absence of a substrate also increases. Fig. 2(b) shows the corresponding 〈Vx〉 vs A. We also plot 〈Vx〉 and 〈Vy〉 vs A for particles with Ax=0 and Ay=A that only move up and down but do not rotate. For the 1D driving, there is no directed motion, as indicated by the curves centered at 〈Vx〉 = 0.0 and 〈Vy〉 = 0.0 in Fig. 2(a,b). For the circular swimmers, there are numerous intervals of A where there is a net dc flow of particles. For 0 < A < 0.52, there is no dc response since the particle orbits are small enough that the particles can move between the barriers without contacting them, as illustrated in Fig. 3(a) at A = 0.49. For 0.52 < A < 0.86, Fig. 2(a,b) indicates that there is net dc motion in both the positive y and positive x directions, with a larger dc response in the y direction, 〈Vy〉 > 〈Vx〉. This interval also includes a plateau region in 〈Vy〉 over which the velocity remains nearly constant, similar to the mode locking phenomenon found for particles driven with asymmetric drives over symmetric periodic substrates [3]. In this regime, as illustrated in Fig. 4(a) at A = 0.57, individual particles fall into a periodic orbit that contacts the barrier once per drive cycle. When the particle is in contact with the barrier, it moves along the bottom of the L shape and is temporarily trapped in the corner of the L until its motion reverses and it moves up by one barrier in the y direction. During successive orbits, the particle channels along the symmetry direction of the lattice so that it moves over by one column in the positive x-direction after six drive cycles. At A=0.75, Fig. 4(b) shows that the particles are guided along the barriers near the corner of the L. We observe the ratio 〈Vy〉/〈Vx〉 = 4.0 at A=0.75 since the particles move six lattice constants in the y direction for every 1.5 lattice constants in the x direction in this locked motion regime.
At A = 0.9, 〈Vy〉 and 〈Vx〉 are zero again in Fig. 2, and in Fig. 3(b) we show the corresponding localized particle orbit in which the particle encircles two barriers without touching them. At A = 1.2 there is still no net dc signal, and the localized particle orbit now encircles three barriers in a single cycle as shown in Fig. 3(c). For 1.3 < A < 1.8, a dc rectification occurs where the particles translate in both the positive x and y directions. For the velocity plateau region centered at A = 1.6, 〈Vy〉/〈Vx〉 = 5.0, and Fig. 4(c) shows that in this region the particle interacts with a single barrier per cycle and also moves past multiple barriers on each cycle. For 1.8 < A < 2.0 we observe a rectification region where the particles move in the positive y and the negative x directions with 〈Vy〉/|〈Vx〉| = 2.0. In this region, as illustrated in Fig. 4(d) for A = 1.9, the particles interacts with three barriers per cycle. The first interaction is with the front of one L-shaped barrier, the second is with the back of another barrier, and the third is with the back corner of yet another barrier.
There are also intervals of A where the particles move strictly in the negative x-direction, such as for 2.035 < A < 2.1. Figure 4(e) shows that in this regime at A = 2.05, the particle interacts with the back of one L-shaped barrier per cycle and translates in the negative x direction. For higher values of A, more complex motions occur. For example, at A = 2.25, illustrated in Fig. 4(f), the particles move in the positive x and y directions with 〈Vy〉/〈Vx〉 = 4.0, and interact with four barriers per cycle. For increasing A, additional rectifying orbits appear that become increasingly complex as the particles interact with larger numbers of barriers per cycle. For most applications, the first few rectifying orbits will likely be the best regimes to consider.
In addition to integer ratios of 〈Vy〉/〈Vx〉, we also observe simple noninteger ratios such as 〈Vy〉/〈Vx〉 = 1.5. In general, for the oblique lattice geometry and counterclockwise swimming particles, 〈Vy〉 is larger than 〈Vx〉. We have only observed very small windows over which the particles move in the negative y direction, and we found no regimes where the particle motion is strictly along the y direction, due to the fact that the easy channel direction along the symmetry axis of the oblique lattice is not aligned with the y direction. The fact that the particles move in different directions for different values of A or orbit radii indicates that particles with different swimming radii but the same chirality could be sorted using the oblique substrate.
There are several differences between this system and the dc rectification induced by driving ac particles over symmetric periodic substrates [2,3]. In the previous work, the substrates were modeled as smooth egg-carton type potentials induced by pinned particles that repelled the remaining particles via a Yukawa interaction potential. In that egg-carton system, the mobile particles are always interacting with the potential substrate, as appropriate for modeling colloidal particles on periodic optical trap arrays [39]. In the present work, the substrate is flat except for the L-shaped barriers, and the particles experience only contact interactions with the barriers. In the egg-carton system under a circular ac drive, a transverse dc motion occurs only if an additional longitudinal dc drift is applied to the particles [2]; if a noncircular ac drive is applied that produces a particle orbit with broken spatial symmetry, then dc rectification can occur even without a dc drift drive [3,5,6]. In the present work, the ac driving orbits are symmetric, and the barrier lattice introduces the asymmetry required for rectification to occur. The system we propose here should be very straightforward to implement due to the simple barrier shapes and particle interactions.

A.  Opposite chirality

Fig5.png
Figure 5: (a) 〈Vy〉 vs A and (b) 〈Vx〉 vs A for the system from Fig. 1(a) with an oblique lattice of L-shaped barriers for clockwise swimming particles with si=−1. The 〈Vy〉 = 0 and 〈Vx〉 = 0 lines are drawn as a guide to the eye. Here, we generally find 〈Vx〉 > 〈Vy〉, the reverse of what is shown in Fig. 2 for counterclockwise swimming particles. The letters a-f indicate the values of A where the particle trajectories in Fig. 6 were obtained.
Fig6.png
Figure 6: The trajectories of a single particle in selected rectification phases for the system in Fig. 5 for clockwise swimming particles with si=−1. The letters a-f in Fig. 5 correspond to the orbits shown in panels (a-f). L-shapes: barriers; dot: individual particle; line: particle trajectory. (a) At A = 1.25, the particle translates in the positive x and y directions. (b) At A = 1.4, the particle translates only in the positive x direction. (c) At A = 1.77, the particle translates only in the negative x direction. (d) At A = 2.08, the particle translates in the positive x direction and negative y direction. (e) At A = 2.15, the particle translates in the positive x and y directions. (f) At A = 2.28, the particle translates only in the positive x-direction.
We next consider the same oblique array of L-shaped barriers but reverse the sign of the drive by setting si=−1 so that the particles move clockwise. In Fig. 5(a,b) we plot 〈Vy〉 and 〈Vx〉 versus A, where we generally find 〈Vy〉 < 〈Vx〉, the opposite of what occurred for the counterclockwise swimming particles. There is also no dc rectification for A < 1.2 for si=−1, whereas for the counterclockwise rotation, rectification occurred down to A=0.52. Figure 5 shows that for 1.2 < A < 1.588, the particles rectify in the positive x and y directions. The trajectory of a particle in this regime is shown in Fig. 6(a) for A=1.25, where the particle interacts with almost the entire length of the front side of the barrier, producing a net translation in the positive x and positive y directions. At A = 1.4, 〈Vy〉 = 0 and the velocity in the x-direction is positive. Here, Fig. 6(b) shows that the particle interacts with two barriers per cycle, once with the front part of the barrier and once with the back part of the barrier. There is an interval of A centered around A = 1.77 where the particles move only in the negative x-direction, and Fig. 6(c) indicates that here the particle encounters only one barrier per cycle and interacts with the back side of the L shape. Near A = 2.08 there is a regime where the particle moves in the positive x direction and the negative y direction, as shown by the particle orbits in Fig. 6(d). Around A = 2.15 the particle moves in both the positive x and y directions again, as highlighted in Fig. 6(e) where the particle interacts with three barriers per cycle. In the region near A = 2.28, Fig. 6(f) shows that the particle translates only in the positive x-direction and interacts with just one barrier per cycle in a manner similar to that found for A = 1.4 [Fig. 6(b)], but in this case the orbits form a much wider arc. For higher values of A similar sets of rectifying motions occur, with the particles typically translating a further distance per cycle, as indicated by the increase in |〈Vx〉| and |〈Vy〉| at higher A in Fig. 5.
Fig7.png
Figure 7: The trajectories of a single particle in the localized regimes for the system in Fig. 5 with clockwise swimming particles. L-shapes: barriers; dot: individual particle; line: particle trajectory. (a) A = 1.15. (b) A = 1.65. (c) A = 2.68.
In the intervals of A where there is no net motion in Fig. 5, the particles adopt localized orbits; however, unlike the counterclockwise case shown in Fig. 3 where the particles undergo circular orbits that do not interact with the barriers, for the clockwise orbits the particles can interact with the barriers but still produce no net translation. For A < 0.5 the particle orbits are small enough to fit between the barriers without contacting them, while for A ≥ 0.5 the orbits can touch the barriers, as shown in Fig. 7(a) for A = 1.15 where the particle interacts with the back of one L and then hits the front of another L while encircling a third barrier. At A = 1.65 the motion is localized and Fig. 7(b) shows that each particle forms an elliptical orbit similar to the one at A = 1.15 where the particle interacts with two barriers during each cycle; in this case, however, the orbit encircles two barriers. For A = 2.68, illustrated in Fig. 7(c), the same type of orbit occurs but the particle encircles ten barriers per cycle.
Fig8.png
Figure 8: (a) ∆y, the difference between 〈Vy〉 for the counterclockwise and clockwise rotating particles, vs A in samples with an oblique lattice of L-shaped barriers. (a) ∆x vs A. In the regions with non-zero mean values of ∆x or ∆y, particles with different swimming chiralities move at different speeds and/or in different directions.
Since the different chiralities produce different modes of motion, the oblique lattice of L-shaped barriers can be used to separate particles moving with different chiralities. In Fig. 8 we plot the velocity differences ∆y=〈Vy〉si=1 − 〈Vy〉si=−1 and ∆x=〈Vx〉si=1 − 〈Vx〉si=−1, where the velocity of the clockwise swimmers is subtracted from the velocity of the counterclockwise swimmers. Whenever ∆y and/or ∆x have a finite value, particles with different chiralities move at different speeds and/or in different directions, and separation of the particles can be achieved.
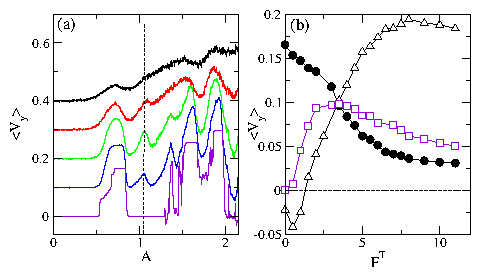
Fig9.png
Figure 9: (a) 〈Vy〉 vs A for the system in Fig. 2 with an oblique lattice of L-shaped barriers and counterclockwise moving particles (si=1) at different thermal force values FT = 0.0, 1.0, 2.0, 4.0, and 6.0, from bottom to top. The curves have been successively shifted up for clarity. The dashed line highlights the appearance of a new peak near A = 1.05 for finite temperature. (b) 〈Vy〉 vs FT for A = 0.75 (circles), which monotonically decreases; A = 1.05 (squares), which starts at 〈Vy〉 = 0, reaches a maximum and then decreases; and A = 2.12 (triangles), which starts with 〈Vy〉 < 0, reverses to a positive value, and then decreases at higher FT.
Fig10.png
Figure 10: The trajectories of a single particle for the system in Fig. 9 with counterclockwise swimming particles and finite temperature. L-shapes: barriers; dot: individual particle; line: particle trajectory. (a) A = 0.9 and FT = 4.0. (b) A = 0.9 and FT = 8.0. (c) A = 1.05 and FT = 0. (d) A = 1.05 and FT = 2.0.


IV.  THERMAL EFFECTS

In Fig. 9(a) we plot 〈Vy〉 versus A for the system from Fig. 2 with an oblique lattice of L-shaped barriers and counterclockwise swimmers for different thermal forces FT=0 to 6.0. In general we find that over ranges of A where plateaus occur at FT=0, 〈Vy〉 decreases in magnitude and the plateau features smear out as FT increases. For ranges of A in which 〈Vy〉 = 0 in the absence of thermal fluctuations, the value of 〈Vy〉 becomes finite when FT is raised above zero. Here, the localized particle orbits become smeared by thermal fluctuations and the particles occasionally interact with extra barriers, producing a nonzero amount of rectification. The magnitude of the peaks in 〈Vy〉 is suppressed by temperature since the thermal kicks can temporarily cause the particles to deviate from their rectifying orbits. For increasing FT, we find some rectification for most values of A, as shown in Fig. 9(a). For example, at A = 0.9 there is no rectification in the absence of thermal fluctuations; however, for FT = 4.0 there is some rectification. Thermally induced rectification is illustrated in Fig. 10(a) for A=0.9 and FT=4.0, where the particle is localized during some time intervals and undergoing net transport in the positive y direction during other time intervals. For high FT, we observe a general decrease in the magnitude of the rectification when the particle trajectories become increasingly random, as shown in Fig. 10(b) for A = 0.9 and FT = 8.0. Over certain ranges of A, the addition of thermal effects create new locking effects that were not present in the zero temperature system. An example of this is highlighted in Fig. 9(a) with a dashed line near A = 1.05. Here, at FT = 0, 〈Vy〉 = 0, but at finite temperature a peak in 〈Vy〉 emerges. This peak persists as the temperature increases before gradually smearing out at high temperatures. In this case, at FT = 0 and A = 1.05, Fig. 10(c) indicates that the particle moves in a circle that just misses interacting with the barriers during each cycle, while when FT = 2.0 for the same value of A, Fig. 10(d) shows that the particles now have a much higher probability of interacting with the barriers. As a result, a finite translation in the positive y direction occurs only for finite temperature.
In Fig. 9(b) we plot 〈Vy〉 versus FT at specific values of A for the system in Fig. 9(a) to highlight the different thermal behaviors. At A=0.75, which is on the first finite rectification plateau, 〈Vy〉 decreases monotonically with increasing FT. At A = 1.05, initially 〈Vy〉 = 0, and 〈Vy〉 gradually increases with increasing FT to a maximum value before decreasing at higher thermal force. At A = 2.12, 〈Vy〉 is negative for FT = 0, and as the thermal force increases, there is a rectification reversal from negative to positive values of 〈Vy〉, which reaches a maximum and then slowly decreases for larger thermal force.
Fig11.png
Figure 11: Samples with an oblique lattice of L-shaped barriers at FT=6.0. Upper curve: 〈Vy〉si=−1 (clockwise particles) vs A. Center curve: 〈Vy〉si=1 (counterclockwise particles) vs A. Lower curve: The corresponding ∆y vs A.
In Fig. 11 we plot 〈Vy〉s=−1 and 〈Vy〉s=1 vs A for the clockwise and counterclockwise swimming particles, respectively, as well as the difference ∆y, which indicates that even at higher temperatures, particles of different chiralities can move in different directions so that separation is still possible.
Fig12.png
Figure 12: (a) 〈Vy〉 vs A and (b) 〈Vx〉 vs A for the system with the square L-shaped barrier array shown in Fig. 1(b) for counterclockwise swimming particles with si=1. (c) 〈Vy〉 vs A and (d) 〈Vx〉 vs A for the same system for clockwise swimming particles with si=−1. The 〈Vy〉 = 0 and 〈Vx〉 = 0 lines are drawn as a guide to the eye. The curves for (a) and (d) are indistinguishable from each other, as are the curves in (b) and (c), indicating that the velocity response is interchanged when the chirality is reversed. The letters a-f correspond to the values of A at which the orbits in Fig. 13 were obtained.
Fig13.png
Figure 13: The trajectories of a single particle in selected rectification phases for the system in Fig. 12 with a square lattice of L-shaped barriers. (a) Counterclockwise swimmers at A=1.25 translate in the y direction. (b) Clockwise swimmers at A=1.25 translate in the x direction. (c) Counterclockwise swimmers at A = 1.75. (d) Clockwise swimmers at A = 1.75. (e) Counterclockwise swimmers at A = 1.95 translate in the y direction. (f) Clockwise swimmers at A = 1.95 translate in the x direction.


V.  OTHER GEOMETRIES

We next consider the case of square lattices of L-shaped barriers, as illustrated in Fig. 1(b). In Fig. 12(a,b) we plot 〈Vy〉 and 〈Vx〉 versus A for this system with counterclockwise moving particles. We find a set of rectification regimes as a function of A that are similar to those in the system with the oblique array of L-shaped barriers, although one notable difference is that for the square lattice it is possible to have dc motion oriented strictly in the y direction, such as at A = 1.35. As was the case for the oblique array, the square array produces some intervals of A where the motion is in the negative x-direction, such as near A = 2.5. When the chirality of the swimmers is reversed in the square array, Fig. 12(c) shows that 〈Vy〉 versus A for the clockwise swimmers has the exact same form as 〈Vx〉 versus A shown in Fig. 12(b) for the counterclockwise swimmers. Similarly, 〈Vx〉 versus A in Fig. 12(d) for the clockwise swimmers has the same form as 〈Vy〉 versus A in Fig. 12(a) for the counterclockwise swimmers. This symmetry in the velocity response is a result of the higher symmetry of the square lattice, which causes the combination of a reversal of the chirality of the swimmer and a 90-degree rotation of the substrate to appear the same as the unrotated and unreversed system, swapping the x and y velocity responses. A similar symmetry is not present in the oblique lattice. The exchange of the velocity response from 〈Vy〉 to 〈Vx〉 with the change in chirality makes the square barrier lattice more convenient than the oblique lattice for particle separation techniques since a measurement of the motion of one chirality of swimmer immediately determines how a swimmer of the opposite chirality will move. For example, if one chirality of swimmer moves strictly in the y direction at a specific value of A, then the opposite chirality of swimmers must move strictly in the x direction for the same value of A. This is illustrated for A = 1.25 in Fig. 13(a), which shows the counterclockwise swimmers translating in the y direction, and Fig. 13(b), which shows the clockwise swimmers undergoing the same motion rotated by 90 degrees, with a resulting translation in the x direction. Similarly, at A = 1.95, Fig. 13(e) shows that the counterclockwise swimmers translate in the y direction while, in Fig. 13(f), the clockwise swimmers translate in the x direction with an orbit of the same shape but rotated by 90 degrees. At A = 1.75, Fig. 12(a,b) shows that counterclockwise swimmers have positive velocities in both the x and y directions with 〈Vy〉 > 〈Vx〉. In the corresponding particle trajectory in Fig. 13(c), the particle moves further in y than in x after several cycles. For the clockwise swimmers at A=1.75, the motion is similar with positive velocities in both the x and y directions, but now 〈Vy〉 < 〈Vx〉, and the corresponding trajectory in Fig. 13(d) is a rotated version of the trajectory in Fig. 13(c).
For both the square and oblique lattices of L-shaped barriers, we also find that for intervals of A where there is no rectification, the application of a dc drift force in one of the directions can induce locking of the motion in the driven direction as well as a transverse rectification. There are also smaller regimes of the external drive where the transverse rectification occurs at different values of the external drive for particles of different chirality, indicating that this could provide another method for particle separation.
Fig14.png
Figure 14: Sample with a square array of line barriers illustrated in Fig. 1(c). (a) 〈Vx〉 (lower dark curve) and 〈Vy〉 (upper light curve) vs A for counterclockwise swimmers. (b) 〈Vx〉 (upper dark curve) and 〈Vy〉 (lower light curve) vs A for clockwise swimmers. For both types of swimmers, 〈Vy〉 ≈ 0 over the entire range of A.
Fig15.png
Figure 15: The trajectories of a single particle in selected rectification phases for the system in Fig. 15 with a square lattice of 1D barriers at A=1.85. (a) Counterclockwise swimmers translate in the negative x direction. (b) Clockwise swimmers translate in the positive x direction.
We have also considered particles moving in a square array of 1D barriers as illustrated in Fig. 1(c). This system has an even higher degree of symmetry than the square lattice of L-shaped barriers, since the barrier lattice now has a rotational symmetry. In Fig. 14(a) and (b) we plot 〈Vx〉 and 〈Vy〉 vs A for the array of 1D barriers for counterclockwise and clockwise swimmers, respectively. In both cases we observe rectification in the x-direction while 〈Vy〉 ≈ 0. The rectification regimes appear at regularly spaced intervals in A, and the rectification is in the negative x direction for the counterclockwise swimmers and in the positive x direction for the clockwise swimmers. Figures 15(a) and (b) illustrate this rectification for the counterclockwise and clockwise swimmers, respectively, at A=1.85 where the particles interact with two barriers per cycle. Both chiralities of swimmers execute orbits with the same shapes, but reversing the chirality flips the orbit by 180 degrees. Although the regime where rectification occurs for the 1D barriers is smaller than that for the L-shaped barriers, the fact that particles of different chirality move in opposite directions through the 1D barriers could make the 1D barrier array the most practical choice for a separation technique.

A.  Barrier lengths

Fig16.png
Figure 16: 〈Vy〉 (solid line) and 〈Vx〉 (dashed line) for a square array of L-shaped barriers with a fixed barrier lattice constant of a = 20 and varied barrier wall length l. (a) l = 18.6. (b) l = 3.0. (c) l = 1.0.
Fig17.png
Figure 17: 〈Vx〉 vs l/a for a square array of L-shaped barriers with a fixed barrier lattice constant of a=20 and varied barrier wall length l. (a) A = 1.25. (b) A = 1.75. (c) A = 2.65.
The value of A determines the radius of the circle in which a particle would move in the absence of any barriers, so as A increases this radius grows linearly. Another length scale in the system is l, the length of an individual barrier wall. For the previous results we fixed l = 5. Here we examine the effect of changing l in the system with a square array of L-shaped barriers. For a fixed barrier lattice constant a, adjacent barriers form a continuous wall for l ≥ a and in this regime no rectification is possible since the particles become completely trapped. In Fig. 16 we plot 〈Vy〉 and 〈Vx〉 versus A for l = 18.6, 3.0, and 1. In general, we find that as l decreases, the width of the rectification regimes decreases, but within each rectification regime, the magnitude of |〈Vy,x〉| is unchanged due to the quantization of the particle orbits. For smaller l, the onset of rectification shifts to higher values of A, as shown in Fig. 16(c), and the windows in which rectification occurs are greatly reduced in extent. In Fig. 17 we plot 〈Vx〉 versus l/a for the same system with fixed a=20 at A = 1.25, 1.75, and 2.65. Here, the rectification can change sign as a function of l/a, and for smaller values of A, the onset of the rectification occurs at larger values of l/a. These results show that the rectification effects for this system are robust for a range of barrier lengths.


VI.  SUMMARY

We have examined circularly swimming particles interacting with periodic arrays of L-shaped or rod-shaped barriers. The particles experience only contact interactions with the barriers, and when in contact with the barrier, a particle moves according to its driving force component that is parallel to the barrier wall. In the absence of barriers, there is no net dc motion. For oblique and square arrays of L-shaped barriers, we observe a rich variety of distinct rectifying phases where dc motion can arise in numerous different directions. These dynamic phases appear as the swimming radius of the particles is varied, and the rectifying phases are associated with periodic orbits in which the particles interact with one or move barriers during each swimming cycle. At certain radii values, the particles become localized and exhibit no net dc rectification. Since the rectification direction varies with swimming radius, such barrier arrays could be used to separate particles with different swimming radii but the same chirality of swimming direction. When the chirality is reversed, the particles rectify in a different set of directions as the swimming radius varies, implying that particles with different chirality can also be separated with the barrier arrays. Our results are robust at finite temperature, and we find that thermal fluctuations can in some cases enhance the rectification by increasing the frequency with which the particles interact with the barriers. For square arrays of L-shaped barriers, the velocity response of counterclockwise swimming particles is rotated with respect to that of clockwise swimming particles, with the y (x) response of the counterclockwise swimmers becoming the x (y) response of the clockwise swimmers. This indicates that in a regime where the counterclockwise swimmers translate strictly in the positive x direction, the clockwise swimmers move strictly in the positive y direction. The symmetry of the velocity response could be used to more readily separate particles of different chiralities. For a square array of 1D barriers, we find that rectification effects still occur over reduced ranges of the swimming radius. For the 1D barrier arrays, the rectification occurs only in one direction for a given chirality, and particles of the opposite chirality move in the opposite direction. Our results could be realized experimentally using the recently studied artificial circle swimmers, swimming bacteria, or other active matter particles that move in circles. Beyond self-driven particles, it should also be possible to create systems of particles that move in circles due to some type of rotating external field.


  ACKNOWLEDGMENTS

We thank J. Drocco for useful discussions. This work was carried out under the auspices of the NNSA of the U.S. DoE at LANL under Contract No. DE-AC52-06NA25396.

References

[1]
P. Reimann, Phys. Rep. 361, 57 (2002).
[2]
C. Reichhardt, C.J. Olson, and M.B. Hastings, Phys. Rev. Lett. 89, 024101 (2002)
[3]
C. Reichhardt and C. J. Olson Reichhardt, Phys. Rev. E 68, 046102 (2003).
[4]
R. Guantes and S. Miret-Artés, Phys. Rev. E 67, 046212 (2003).
[5]
D. Speer, R. Eichhorn, and P. Reimann, Phys. Rev. Lett. 102, 124101 (2009).
[6]
R. Chacón and A. M. Lacasta, Phys. Rev. E 82, 046207 (2010).
[7]
P. Tierno, T.H. Johansen, and T.M. Fischer, Phys. Rev. Lett. 99, 038303 (2007).
[8]
P. Tierno, T.H. Johansen, and F. Sagués, Phys. Rev. E 80, 052401 (2009).
[9]
B. ten Hagen, S. van Teeffelen, and H. Löwen, J. Phys.: Condens. Matter 23, 194119 (2011); P. Romanczuk, M. Bär, W. Ebeling, B. Lindner, and L. Schimansky-Geier, Eur. Phys. J. Special Topics 202, 1 (2012); M.C. Marchetti, J.-F. Joanny, S. Ramaswamy, T.B. Liverpool, J. Prost, M. Rao, and R.A. Simha, arXiv:1207.2929.
[10]
P. Galajda, J. Keymer, P. Chaikin, and R. Austin, J. Bacteriol. 189, 8704 (2007).
[11]
G. Mahmud, C.J. Campbell, K.J.M. Bishop, Y.A. Komarova, O. Chaga, S. Soh, S. Huda, K. Kandere-Grzybowska, and B. A. Grzybowski, Nature Phys. 5, 606 (2009).
[12]
W.F. Paxton, K.C. Kistler, C.C. Olmeda, A. Sen, S.K. St. Angelo, Y.Y. Cao, T.E. Mallouk, P.E. Lammert, and V.H. Crespi, J. Am. Chem. Soc. 126, 13424 (2004).
[13]
J.R. Howse, R.A.L. Jones, A.J. Ryan, T. Gough, R. Vafabakhsh, and R. Golestanian, Phys. Rev. Lett. 99, 048102 (2007).
[14]
S.J. Ebbens and J.R. Howse, Soft Matter 6, 726 (2010).
[15]
H.-R. Jiang, N. Yoshinaga, and M. Sano, Phys. Rev. Lett. 105, 268302 (2010).
[16]
G. Volpe, I. Buttinoni, D. Vogt, H.J. Kümmerer, and C. Bechinger, Soft Matter 7, 8810 (2011).
[17]
I. Buttinoni, G. Volpe, F. Kümmel, G. Volpe, and C. Bechinger, J. Phys.: Condens. Matter 24, 284129 (2012).
[18]
I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert, and L. Bocquet, Phys. Rev. Lett. 108, 268303 (2012); G.S. Redner, M.F. Hagan, and A. Baskaran, Phys. Rev. Lett. 110, 055701 (2013); J. Palacci, S. Sacanna, A.P. Steinberg, D.J. Pine, and P.M. Chaikin, Science 339, 936 (2013); I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger, and T. Speck, Phys. Rev. Lett. 110, 238301 (2013).
[19]
M.B. Wan, C.J. Olson Reichhardt, Z. Nussinov, and C. Reichhardt, Phys. Rev. Lett. 101, 018102 (2008).
[20]
J. Tailleur and M.E. Cates, Europhys. Lett. 86, 60002 (2009).
[21]
I. Berdakin, Y. Jeyaram, V.V. Moshchalkov, L. Venken, S. Dierckx, S.J. Vanderleyden, A.V. Silhanek, C.A. Condat, and V.I. Marconi, Phys. Rev. E 87, 052702 (2013).
[22]
P. Galajda, J. Keymer, J. Dalland, S. Park, S. Kou, and R. Austin, J. Mod. Opt. 55, 3413 (2008).
[23]
V. Kantsler, J. Dunkel, M. Polin, and R.E. Goldstein, Proc. Natl. Acad. Sci. (USA) 110, 1187 (2013).
[24]
A. Pototsky, A.M. Hahn, and H. Stark, Phys. Rev. E 87, 042124 (2013).
[25]
L. Angelani, R. Di Leonardo, and G. Ruocco, Phys. Rev. Lett. 102, 048104 (2009); R. Di Leonardo, L. Angelani, D. Dell'Arciprete, G. Ruocco, V. Iebba, S. Schippa, M.P. Conte, F. Mecarini, F. De Angelis, and E. Di Fabrizio, Proc. Natl. Acad. Sci. (USA) 107, 9541 (2010); A. Sokolov, M.M. Apodaca, B.A. Grzyboski, and I.S. Aranson, Proc. Natl. Acad. Sci. (USA) 107, 969 (2010).
[26]
H. C. Berg, Random Walks in Biology (Princeton University Press, Princeton, NJ, 1983).
[27]
M.E. Cates, Rep. Prog. Phys. 75, 042601 (2012).
[28]
W.R. DiLuzio, L. Turner, M. Mayer, P. Garstecki, D.B. Weibel, H.C. Berg, and G.M. Whitesides, Nature 435, 1271 (2005).
[29]
E. Lauga, W.R. DiLuzio, G.M. Whitesides, and H.A. Stone, Biophys. J. 90, 400 (2006).
[30]
J. Hill, O. Kalkanci, J.L. McMurry, and H. Koser, Phys. Rev. Lett. 98, 068101 (2007).
[31]
I.H. Riedel, K. Kruse, and J. Howard, Science 309, 300 (2005).
[32]
B.M. Friedrich and F. Jülicher, New J. Phys. 10, 123025 (2008).
[33]
S. van Teeffelen, U. Zimmermann, and H. Löwen, Soft Matter 5, 4510 (2009).
[34]
R. Ledesma-Aguilar, H. Löwen, and J.M. Yeomans, Eur. Phys. J. E 35, 70 (2012).
[35]
R. Di Leonardo, D. Dell’Arciprete, L. Angelani, and V. Iebba, Phys. Rev. Lett. 106, 038101 (2011).
[36]
A. Kaiser and H. Löwen, Phys. Rev. E 87, 032712 (2013).
[37]
F. Kümmel, B. ten Hagen, R. Wittkowski, I. Buttinoni, R. Eichhorn, G. Volpe, H. Löwen, and C. Bechinger, Phys. Rev. Lett. 110, 198302 (2013).
[38]
M. Mijalkov and G. Volpe, arXiv:1212.6504.
[39]
T. Bohlein, J. Mikhael, and C. Bechinger, Nature Mater. 11, 126 (2012).


File translated from TEX by TTHgold, version 4.00.

Back to Home