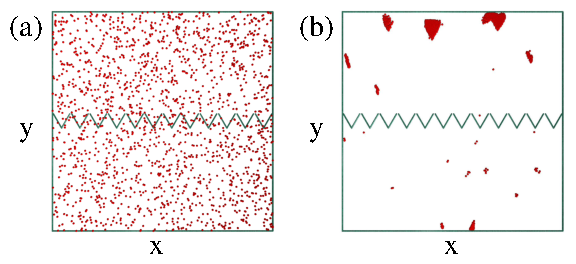
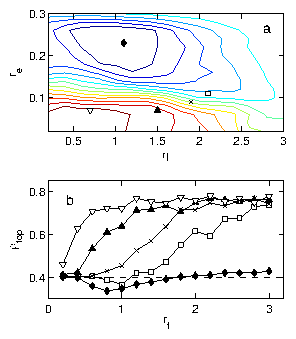
 Figure 3: (Color online) Dependence of rectification behavior on re, η, and rf
for a sample with ρ0=0.4.
(a) Rectification phase diagram for re vs η with rf
fixed at rf=1.0. Contours indicate lines of constant ρtop.
Lower contours (red) indicate rectification into the top
chamber and upper contours (blue) indicate rectification to the bottom
chamber. (b) Rectification curves
showing ρtop after
4×105 time steps in the same system as
a function of rf for various selections of
re and η: re=0.23, η = 1.1 (black lozenges);
re=0.11, η = 2.1 ([¯]); re=0.09, η = 1.9 (x);
re=0.07, η = 1.5 (black triangles); re=0.07, η = 0.7
(big down triangles). The initial density ρ0=0.4 is indicated by a
dashed line. The location of each curve on the re vs η
phase diagram in (a) is indicated by the corresponding symbol; the
point corresponding to the lowest curve (black lozenges) sits at
the maximum of reversed rectification, and the remaining points ([¯],
x, black triangles, and big down triangles) successively ascend
the landscape to the peak of forward rectification.
Figure 3: (Color online) Dependence of rectification behavior on re, η, and rf
for a sample with ρ0=0.4.
(a) Rectification phase diagram for re vs η with rf
fixed at rf=1.0. Contours indicate lines of constant ρtop.
Lower contours (red) indicate rectification into the top
chamber and upper contours (blue) indicate rectification to the bottom
chamber. (b) Rectification curves
showing ρtop after
4×105 time steps in the same system as
a function of rf for various selections of
re and η: re=0.23, η = 1.1 (black lozenges);
re=0.11, η = 2.1 ([¯]); re=0.09, η = 1.9 (x);
re=0.07, η = 1.5 (black triangles); re=0.07, η = 0.7
(big down triangles). The initial density ρ0=0.4 is indicated by a
dashed line. The location of each curve on the re vs η
phase diagram in (a) is indicated by the corresponding symbol; the
point corresponding to the lowest curve (black lozenges) sits at
the maximum of reversed rectification, and the remaining points ([¯],
x, black triangles, and big down triangles) successively ascend
the landscape to the peak of forward rectification.
|